|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Borwein P. — Computational Excursions in Analysis and Number Theory |
|
|
 |
| Предметный указатель |
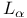 3 3
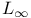 3 3
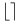 156 156
![$\mathbb{Z}[z]$](/math_tex/a9493d775e6d58ed5693cc692a1dfe0082.gif) 2 2
![$\mathbb{Z}_p[z]$](/math_tex/67bbccb2486e2ff43bffc52829f53f5382.gif) 2 2
 2 2
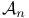 2 2
 2 2
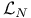 2 2
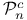 2 2
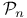 2 2
 2 2 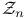 1 1
Acyclic autocorrelation 6 109
Algebraic integer 15 80
Approximating zeros 67
Atkinson, F. 104
Autocorrelation coefficient 109 115
Average norms of polynomials 32
Barker polynomial 6 34 109 128 196
Basic PSLQ algorithm 173
Beck, J. 127
Bernasconi Model 122
Bernstein-type inequality for rational functions 146
Bernstein-type inequality in 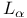 142 142
Bernstein’s inequality for trigonometric polynomials 142
Bernstein’s inequality on the disk 142
Bombieri’s norm 151
Boyd, D. 17 20 60 64
Boyd’s algorithm 25
Boyd’s conjecture 20
Byrnes, J. 66
Cauchy’s integral formula 4
CHARACTER 182
Character polynomial 182
Character, primitive character 182
Chebyshev polynomials 56 75
Chebyshev polynomials of the second kind 56
Chebyshev’s inequality 143
Chernick, J. 88
Choi, S. viii
Chudnovsky, G. 79 83 200
Classes of polynomials 1
Closure of measures problem 6
Cohen, H. 154
Conjecture of Boyd 20
Conjecture of Erdos 127
Conjecture of Erdos and Szekeres 103
Conjecture of Konyagin 128
Conjecture of Littlewood 124
Conjecture of Montgomery 79
Conjecture of Schinzel and Zassenhaus 6 20 196
Conjecture of Wright 87
Conjecture on Barker polynomials 110
Conjecture on bounded merit factors 122
Conrey, B. 40 182
Cyclotomic polynomial 15 43 124
de Bruijn, N.G. 49 143
Denseness of zeros 72
Diophantine approximation 67
Dirichlet box argument 23
Distribution of zeros 54
Dobrowolski, E. 16
Easier Waring problem 95 97 201
Elliptic curve 90
Enestrom — Kakeya theorem 148
Equal sums of like powers 85
Equioscillation property 56
Erdos — Szekeres problem 5 103 195
Erdos, another problem 64
Erdos, P. 133
Erdos, problem for real trigonometric polynomials 127
Erdos, problem in 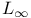 5 5
Even ideal symmetric solution 86
Everest, G. 143
Expected  norm 125 norm 125
Explicit merit factor formulae 181
Fejer’s theorem 149
Fekete polynomial 37 123 181
Fekete polynomial, shifted 123
Fekete, M. 76
Ferguson, H. 153 157
Ferguson, R. viii
Flat polynomials 127
Forcade, R. 153 157
Fractal set 73 199
Gauss sum 182
Gauss, K.F. 38
Ghate, E. 17
Golay and Harris heuristic 130
Golay complementary pair 31 109—111
Golay, M. 6 124 182
Golden mean 23
Golomb ruler problem 129
Gongalves’s inequality 148
Gorshkov — Wirsing polynomials 78 79
Gorshkov — Wirsing polynomials on [0, 1] 81
Graeffe’s root powering method 44
Gray codes 9
Guy, R. 64
H(p) 4
Habsieger, L. 77 79
Hadamard’s inequality 105
Hare, K. viii
Hastad, J. 169
Height 2 3 142
Hilbert, D. 1 76
Hironaka, E. 17
HJLS 153 169 170
Holder’s Inequality 4
Ideal solution 86 97 103
Inequality for factors 150
Inequality for length and height 148
Inequality for measure 148
Inequality for reciprocal polynomials 145
Inequality for zeros 148
Inequality of Bernstein 142
Inequality of Chebyshev 143
Inequality of Holder 4
Inequality of Markov 143
Inequality, involving coefficients 147
Integer Chebyshev constant 75 76
Integer Chebyshev problem vii 5 12 195
Integer relation 12 106
Integer relation, algorithms 153
Integer transfinite diameter 75 84
Jacobi symbol 182
Jedwab, J. viii 119
Jensen’s theorem 3—5
Joo, I. 133
Just, B. 169
Kahane, J.-P. 127
Kapoor, V. viii
Kashin, B. 76
Kneser’s inequality 150
Knuth, D. 9
Komornik, K. 133
Konyagin, S. 125 128
Konyagin’s conjecture 128
| Kronecker’s theorem 15 43 51
L(p) 4
Lagarias, J. 169
Lattice vii 11 77 153
Lattice, basis reduction algorithm 153
Lau, K.-S. 136
Lax-type inequality 146
Lax’s inequality 144
Legendre symbol 37 122 181
Lehmer’s conjecture 62
Lehmer’s problem vii 6 17 196
Length 3 142
Lenstra, Lenstra, and Lovasz 11 154
Limit points of Salem numbers 22
Littlewood polynomials 2 43 121
Littlewood polynomials, random 125
Littlewood’s conjecture 124
Littlewood’s problem 5 121 126 195
Littlewood’s problem in 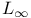 126 126
LLL algorithm 12 153 156
Location of zeros 53
Lorentz, G.G. 143
Loreti, P. 135
Lucas’s theorem 150
m(P) 3
Mahler measure 3 15
Mahler’s problem 6 20 196
Maier, H. 52
Malik, M. 144
Maltby, R. 104 106
Markov’s inequality 77 143
Maximum multiplicity of the vanishing at 1 60 61
McCollum, S. viii
Meichsner, A. viii 153
Mercer, I. viii
Merit factor 115 122 123 182
Merit factor problem 6 110 196
Mignotte, M. 148
Monk integer Chebyshev polynomials 82
Montgomery question 7 79 197
Montgomery, H. 38 78
Mossinghoff, M.J. 17 25
Multiplicative 3 46 51 189
Multivariate Mahler measure 17
Nazarov, M. 126
Negative reciprocal polynomial 16
NP-hard 11
Odd ideal symmetric solution 86
Odlyzko question 65
Odlyzko, A. 63 126
Open problems 195
Parseval’s formula 17
Pedicini, M. 135
Pellet’s theorem 149
Pentagonal number theorem 106
Perron number 24
Pinner, C. 25 67
Pisot number 15 133
Polynomial, average norm 32
Polynomial, Barker polynomial 6 34 109
Polynomial, Chebyshev polynomials 56 75
Polynomial, classes of polynomials 1
Polynomial, cyclotomic polynomial 15 43
Polynomial, Fekete polynomial 37 123
Polynomial, Littlewood polynomials 2 43 121
Polynomial, negative reciprocal polynomial 16
Polynomial, reciprocal polynomial 6 16
Polynomial, Rudin — Shapiro polynomials 27
Polynomial, self-inversive polynomial 16
Polynomial, shifted Fekete polynomials 40
Polynomial, skewsymmetric polynomial 32
Polynomial, symmetric polynomial 8
Polynomial, Turyn-type polynomials 123
Poonen, B. 63
Pott, A. 119
Primitive character 182
Pritsker, I. 79
Products of cyclotomic polynomials 43
Prouhet — Tarry — Escott problem 5 12 85 97 103 195
Pseudocode for HJLS 170 172
Pseudocode for LLL 156
Pseudocode for PSLQ 160
PSLQ algorithm 11 12 153 157 160
Quadratic character 37
Quadratic reciprocity theorem 41
Random Littlewood polynomial 125
Reciprocal polynomial 6 16
Reduced basis 11
Research problems 195
Rhin, G. 25 197
Riemann hypothesis is false 9
Riesz’s identity 143
Robinson, L. 126
Rouche’s Theorem 4
Rudin — Shapiro polynomials 27 37 112 122 126
Saffari, B. 116 126
Salem number 15
Salvy, B. 77 79
Schinzel, A. 16
Schinzel’s theorem 19
Schmidt, B. 116
Schnorr, C.P. 169
Schur — Siegel — Smyth trace problem 7 79 197
Schur, I. 79
Schur’s Theorem 53
Self-inversive polynomial 16
Self-inversive polynomial, Barker polynomials 116
Shapiro, H. 27 144
Shifted Fekete polynomials 40 42 123
Siegel zero 40
Skewsymmetric polynomial 32 123
Smallest Pisot number 16
Smallest Salem number 16
Smyth, C. viii 16 79 90
Smyth’s theorem 17
Smyth’s theorem, weak form 17
Solomyak, B. 135
Spectra 133
Supremum norm 3 141
Symmetric polynomial 8
Szasz’s inequality 147
Szego’s theorem 149
Turyn, R. 116 117 122
Turyn-type polynomials 123 182 192
Vaaler, J. 25
Vandermonde determinant 105
Vaughan, R. 100
Visser’s inequality 147
von Golitschek, M. 143
Voutier, P. 16
Walsh’s two-circle theorem 150
Ward, T. 143
Waring problem 97
Waring problem, easier Waring problem 97 201
Weak form of Smyth’s theorem 17
Wooley, T. 100
Wright, E.M. 85 87 97
Zassenhaus, H. 20
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



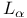
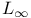
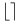
![$\mathbb{Z}[z]$](/math_tex/a9493d775e6d58ed5693cc692a1dfe0082.gif)
![$\mathbb{Z}_p[z]$](/math_tex/67bbccb2486e2ff43bffc52829f53f5382.gif)

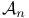

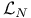
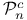
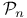
 2
2 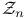
 norm
norm