|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Brauer F., Nohel J.A. — The qualitative theory of ordinary differential equations |
|
|
 |
| Предметный указатель |
A priori bound 37
Abel's formula 46 48 57
Abel's theorem 100
Absolute stability 267—273
Acceleration 1
Acceleration, due to gravity 2
Air resistance 3 5 8 9 201
Almost linear system 144 160—171 184 185 201 261
Almost linear system, perturbed 237
Almost linear system, stability of 143—151 160—171
Amplitude 238 239 244 245 251
Asymptotic behavior of solutions 159 165 178
Asymptotic behavior of solutions of linear systems with constant coefficients 80—83
Asymptotic equivalence 144 159 178—183
Asymptotic stability 147 150—152 155 159 160 169 170 180 184 197 199 202 205 209 232 234
Asymptotic stability, criteria of 185
Asymptotic stability, extent of 215—228
Asymptotic stability, global 215—228 271 272
Asymptotic stability, of equilibrium solution 146
Asymptotic stability, of unperturbed system 169
Asymptotic stability, of zero solution 150 151
Asymptotic stability, region of 149 168 187 196 201 215—220 222 223
Asymptotic stability, uniform 147 169
Attractor 95 103 154 163 164
Autonomous equation 149 188
Autonomous perturbations 183
Autonomous systems 83—95 145 149 150 159 185 192 193 195 209 211 234 256
Autonomous systems, nonlinear 160
Autonomous systems, perturbed 163
Autonomous systems, stability of 192
Autonomous systems, two-dimensional 163 171
Averaging, method of 237 261
Basis 62 63 76 274 275 280 281
Basis for vector space 42
Bessel equation 180
Bessel functions 180
Boundary 25
Boundary points 25
Boundedness 223 225
Canonical form 77 78 171 274—283 290 292
Canonical form, diagonal 76 275
Canonical form, Jordan 73—80 279 282 283
Canonical form, of 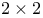 matrices 284—289 matrices 284—289
Canonical form, real 292
Cauchy convergence criterion 56 131
Center 95 103 164
Chain rule 110 123 194
Change of variable 73
Characteristic exponents 98—101 159
Characteristic function 262
Characteristic function, admissible 262 263 264 267 269 273
Characteristic function, Characteristic polynomial 60 68 71 74 152 155 278 279
Characteristic function, linear 271
Characteristic roots See Eigenvalues
Characteristic values 60
Circuit 10
Coefficient matrix 67 70 75 95
Cofactors 35
Column vector 15 33 34 45
Comparison Test 116
components 34
Components of region 197 211
Components of set 211
Conditional stability 171—178
Conditional stability of zero solution 172
Conservation of energy 189
Conservative mechanical system 188 189
Constant coefficients 55
Continuation 130 131 133 192 206
Continuation of solutions 127—135
Continuity 24—30
Continuity of solutions 28 30 108
Continuity of vector functions 19
Continuous dependence on initial conditions 137 148
Continuous dependence on initial values 212
Control 261
Control system 267 272
Control theory 223
Control, admissible 270
Controllability 237
Convergence 19
Convergence, absolute 116
Convergence, of successive approximations 114
Convergence, uniform 116 134
Critical points 85 86 90 95 145 147 160 187 191 192 200 201 211 252 264 269
Critical points, isolated 191 197
Critical points, stability of 184
Critical points, unstable 253
Current 9
Damping 225 251
Damping term 191
Dependence on initial conditions and parameters 135—142
Derivative of V with respect to system 193 194 209
Derivative of vector function 20
Determinant 34 35 47—49 154 155 265 296
Determinism 23
Diagonal matrix See Matrix
Differentiability, of vector functions 19
DIMENSION 65 274 277—279 281
Dimension of vector space 41
Direct control 272
Direct control problem 273
Direct method 187
Direct sum 277 279
Direct sum of subspaces 64
Direction field 259
Dirichlet 187
Dissipation of energy 191
Distance between two vectors 19
Distance function 19
Dynamical system 85
Eigenvalues 60—65 70 71 74—76 81 90 95 98 100 104 105 151—153 156 158 159 161—165 171 172 179—181 183 185 200 261 264 265 270 271 275—279 287 284 300
Eigenvalues, complex 287 288
Eigenvalues, distinct 76 78 276
Eigenvalues, double 77 286
Eigenvalues, generalized 276
Eigenvalues, multiple 77 81 153
Eigenvalues, multiplicity 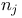 64 64
Eigenvalues, multiplicity of 65 66 68 76 80 278 282 290
Eigenvalues, multiplicity two 61
Eigenvalues, of matrix 60
Eigenvalues, simple 77
Eigenvector 61—63 75 76 274 275 278 279 287 288
Eigenvector, corresponding 61—63 276
Eigenvector, generalized See Generalized eigenvectors
Eigenvector, linearly dependent 275 277 286
Eigenvector, linearly independent 62—64 75 76 78 275 276 286
Electrical system 205
Elliptic integral 245
Energy function 238 245 247 248 252 254
Equation of motion 5 8 9
Equation of n-th order 14
Equation of pendulum 6
Equilibrium 4 9 107 146 151 168 169 197
Equilibrium point 145 190 191 197 250
Equilibrium point, asymptotically stable 147
Equilibrium point, conditionally stable 178
Equilibrium point, Equilibrium position 3 8 146 196
Equilibrium point, stable 147
Equilibrium point, unstable 147 178 245
Equilibrium solution 145 198
Equilibrium solution, asymptotically stable 146
Equilibrium solution, stable 146
Equilibrium solution, unstable 146
Equilibrium state 86 145
Equivalent integral equation 156
Equivalent system 13 14 73 95 153 220 223 224 228 230 233 248 267
Equivalent system of first-order equations 54 105
Equivalent system of n first-order equations 54
Euclidean distance 19
| Euclidean length 17 18
Euclidean norm 24 205
Euclidean space 10 16 26
Existence and uniqueness for linear systems 37—39
Existence and uniqueness of solutions 29
Existence of solutions 24—30 108 111 119 120 130 133 145
Existence of solutions, bounded 179
Existence of solutions, of initial value problem 118
Existence of solutions, of scalar differential equations 108—122
Existence of solutions, periodic 101 237
Existence problem 23
Existence theory 108—142
Existence theory for systems of first-order equations 122—124
Experimental error 164
Exponential of matrix 55 79
Feedback 272
Feedback control signal 262
Feedback electronic circuit 251
Finite basis 42
Fixed point theorem 237
Floquet's theorem 96 97 185
Forcing term 51
Forcing vector, periodic 102
Friction 251
Function V 193 195 201 202 209 211 213 217 221 223 224 227 228
Function V, negative definite 193 195 201 202 224 229 231 232 234 266 269
Function V, positive definite 193 195 196 198 200 202 205 207—209 211 214 215 217 221 224 228—232 234 268 269
Function, linear independence of 41
Function, vector-valued 20 21
Fundamental matrix 45 46 48—55 57 60 62 64 66 67 69—72 74 78 80 86 96 99 102—105 151 152 159
Fundamental set of solutions 44
Fundamental theorem of calculus 24 53 109 241
General solution 55 71 73 104 105 107
Generalized eigenvalues 276
Generalized eigenvectors 274—283
Generalized eigenvectors, index of 277
Global result 134
Gravitational attraction 3 5
Gravitational force 2
Gravity 8
Gronwall inequality 30—32 38 125 126 136 137 140 156 157 162 165
Hamiltonian form 189
Hamiltonian systems 169 189
Homogeneous equation 54
Homogeneous system See Linear systems
Hooke's law 3 5 7 9
Identity matrix 34 55 77 102
Improper integral 240
Improper node 90 93
Index, theory of 237
Indirect control 272
Inductance 10
Infinitesimal upper bound 231 232 234
Inhomogeneous system See Linear systems
Initial condition 4 9 21—23 26 30 37 38 43 53 54 108 110 124 134 135 162 176 192 205
Initial condition, continuity of solution with respect to 24
Initial displacement 247
Initial position 250
Initial value 9 196
Initial value problem 9 11 26—28 72 109 110 124 126 145 175 192
Initial velocity 3 247 250
Instability 152 196 205
Instability of equilibrium solution 146
Integrability of vector functions 19
Integral equation 109—111 116—118 124 130 131 137 141 162 173 174 176 179 182 183
Integral equation of Volterra type 109
Integral equation, equivalent to initial value problem 110
Integral of system 189
Invariance under translations of time 84 85 147 192 205
Invariant 76
Invariant set 208—216 234
Invariant subset 215 218 222 224 235 236
Invariant subspace 274—283
Inverse matrix See Matrix
Jordan canonical form 73—80 279 282 283
Jordan canonical matrix 282 283
kinetic energy 188 194 197
Kirchoff's law 9 106
l'Hopital's rule 203
Lagrange 187
Lagrange stability 223 224
Lagrange's theorem 188 190
Laplace transform 82
Levinson, N. 180
Lienard 259
Lienard equation 191 201 202 205 209 214 217 219 224 225 237
Lienard equation, periodic solutions of 250—261
Limit cycle 222
Limit point of orbit 211
Limiting autonomous system 235 236
Linear approximations 187
linear combination 41
Linear combination of solutions 44
Linear combination of vectors 42
Linear dependence 41
Linear dependence of functions 41
Linear differential equations, first-order 12
Linear differential equations, second-order 13
Linear homogeneous scalar equation 45
Linear independence 41 44 64 274
Linear independence of functions 41
Linear systems 34 37 65 66 80 95 96 133 149 151—159 161 200
Linear systems, algebraic 277
Linear systems, control of 263
Linear systems, homogeneous 39—53 55 72 102 107
Linear systems, homogeneous, algebraic 63
Linear systems, homogeneous, associated 54
Linear systems, homogeneous, corresponding 51 54 55
Linear systems, homogeneous, of first-order equations 50
Linear systems, inhomogeneous 54 55
Linear systems, nonhomogeneous 51—55 101 104 107
Linear systems, nonhomogeneous, of algebraic equations 102
Linear systems, of differential equations 33
Linear systems, stability of 143—159
Linear systems, stability properties of 187
Linear systems, two-dimensional 147
Linear systems, two-dimensional, with constant coefficients 89
Linear systems, unperturbed 169 170
Linear systems, with constant coefficients 55—74 82 84 89 98 185
Linear systems, with periodic coefficients 50 96—107 185 290
Linear systems, with variable coefficients 155
Linear unperturbed equation 170
Linearization 144
Linearized system 200
Linearly dependent eigenvectors 275 277 286
Linearly dependent set of vectors 41
Linearly independent columns 48
Linearly independent eigenvectors 62—64 75 76 78 275 276 286
Linearly independent points 43
Linearly independent set of vectors 41—44
Linearly independent solutions 43—45 54 62 64 69 70 153 172
Linearly independent solutions of homogeneous equations 54
Liouville transformation 141
Lipschitz condition 112 115 117 119 123 125 126 139 140
Lipschitz constant 113 123 140
Local existence theorem 114
Local problem 108
Logarithm of matrix 50 290—295
Lur'e problem 237
Lyapunov second method 150 169 187—236 262 266
Lyapunov theorem 191—208 231
Lyapunov theorem, on matrices 265 266 299
Lyapunov theorem, proof of 205—208
Lyapunov, A.M. 143 187
Mass 7 14
Mass-spring system 1—7 9 22 201
Mass-spring system, coupled 7—10 30
Mathematical model 1 3 6 23 24 108
Mathematical model for mass-spring system 5 22
Matrix 15 33 37
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



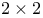 matrices
matrices