|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| David H., Nagaraja H. Ч Order Statistics (Wiley Series in Probability and Statistics) |
|
|
 |
| ѕредметный указатель |
Logistic distribution 358
Logistic distribution, BLUE in 364
Logistic distribution, estimation of parameters in 364
Logistic distribution, generalized 52
Logistic distribution, moments of Order statistics in 358
Logistic distribution, optimal spacing of Order statistics in 295
Logistic distribution, percentage points of Order statistics in 355
Lognormal distribution, estimation of parameters in 364
Lognormal distribution, moments of Order statistics in 358
Lognormal distribution, percentage points of Order statistics in 355
Lorenz curve 90Ч91
m-dependent processes 288 309Ч310
Majorization 103Ч104
Markov chain, order statistics as a 17Ч20 154 174
Markov chain, record values as a 31Ч32
Maxima, ratio of 178
Maxima, statistics expressible as 125Ч133 149Ч152
Maximum likelihood (ML) methods, for censoring and truncation 193Ч202
Maximum, 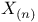 , ,  , ,  in multinomial 151 in multinomial 151
Maximum, 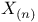 , ,  , ,  of exchangeable variates 102Ч103 of exchangeable variates 102Ч103
Maximum, 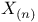 , ,  , ,  , asymptotic distribution of 22 296 , asymptotic distribution of 22 296
Maximum, 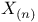 , ,  , ,  , bounds for moments of 60Ч63 119 , bounds for moments of 60Ч63 119
Maximum, 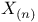 , ,  , ,  , distribution of 26 , distribution of 26
Mean deviation, in normal samples 250
Mean deviation, robustness of 212
Median 2
Median absolute deviation (MAD) 223
Median Filter 141
Median for Cauchy distribution 54
Median in life testing 191
Median in normal samples 241Ч242 277
Median of pairwise means 215
Median, asymptotic properties 285 288
Median, confidence intervals for 159Ч162 362
Median, distribution of (n even) 28
Median, efficiency of 93 241Ч242
Median, moving 140
Median, multivariate 164 169
Median, percentage points for various populations 356
Median, population 5 45
Median, sample 2 23 241Ч243
Midmean 217 235Ч237
Midrange (=midpoint) 15
Midrange in uniform distribution 175 320
Midrange, asymptotic distribution of 326Ч327
Midrange, distribution of 26Ч27
Midrange, properties of 242
Minimum  , ,  , application of 284 , application of 284
Minimum  , ,  , asymptotic distributions of 303 , asymptotic distributions of 303
Mode, estimation of 290
Moments of Order statistics 33Ч44 49Ч55
Moments of Order statistics, approximations for 70Ч74 83Ч86
Moments of Order statistics, bootstrap estimation of 183Ч5 227Ч228
Moments of Order statistics, bounds for 60Ч74
Moments of Order statistics, discrete case 42Ч44
Moments of Order statistics, existence of 34 54
Moments of Order statistics, normal case 40Ч42 53
Moments of Order statistics, recurrence relations between 44Ч49 55Ч58
Moments of Order statistics, relations between 38Ч39 49Ч52
Moments of Order statistics, tables of 356Ч360
Monte Carlo methods in robustness studies 217 223
Monte Carlo methods, Order statistics in 15 31
Moving order statistics 140Ч141
Multinomial distribution, maximum variate in 151
Multinomial distribution, moments of extremes 360
Multinomial distribution, range in 261Ч262
Multiple comparisons 3
Multiple comparisons based on range 253Ч256
Multiple decision procedures 3
Multivariate asymptotic distribution of Order statistics 313Ч315
Multivariate data, ordering of 13
Multivariate extreme deviate 131
Multivariate inequalities 133
Multivariate medians 164 169
Multivariate normal distribution see also УEquicorrelated normal variatesФ
Multivariate normal distribution, censoring of 203
Multivariate normal distribution, Order statistics in 13 100Ч102
Multivariate tolerance regions 166
NBU, New better than used 76 90
NBUE: NBU in expectation 91
Negative binomial distribution 360
Nonparametric inference 159Ч170
Normal distribution see also УBivariate normal distributionФ; УMultivariate normal distributionФ
Normal distribution, asymptotic distribution of maximum in 302
Normal distribution, asymptotic estimation in 339Ч340
Normal distribution, bounds and approximations for 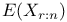 80Ч86 80Ч86
Normal distribution, cdf of extremes in 355
Normal distribution, cdf of range in 356
Normal distribution, coefficients of BLUE in 363
Normal distribution, contaminated 360
Normal distribution, independence of mean and range 18Ч19
Normal distribution, linear estimators of  and and  for 189Ч190 for 189Ч190
Normal distribution, moments of Order statistics 40Ч42 356
Normal distribution, optimal spacing of Order statistics in 294Ч295 317
Normal distribution, percentage points of Order statistics in 355
Normal distribution, probability plotting for 270Ч271
Normal distribution, quick estimators of  and and  for 241Ч250 for 241Ч250
Normal distribution, robust estimation of  and and  for 211Ч216 for 211Ч216
Normal distribution, tests of 272Ч273 365
Notation 4Ч7
Optimal asymptotic estimation by Order statistics 335
Optimal choice (spacing) of Order statistics in large samples 290Ч296
Optimal choice (spacing) of Order statistics in large samples, tables for normal parent 366
Optimal choice (spacing) of Order statistics in large samples, tests under 296
Order statistics see УDistribution of Order statisticsФ and under specific statistics and specific distributions
Order statistics, fractional 21 162
Order statistics, generalized 21Ч22
Orthonormal system 70
Outliers 3
Outliers, robust estimation in presence of 218Ч223 236Ч237
Outliers, tables of tests for 360Ч362
P-P plot 272
Pareto distribution 52
Pareto distribution, k-variate 117
Pareto distribution, moments of Order statistics in 52 360
Pareto distribution, optimal spacing of Order statistics in 295
Partial sums of concomitants 348 353
Peak to median ratio 27
Peakedness 77
Percentage points see under specific statistics and specific distributions
Permanent (of a matrix) 98 113
Poisson distribution, range in 261Ч262
Pooled rms estimator of 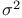 121 121
Power-function distribution 52
Power-function distribution, characterization 157
Power-function distribution, optimal spacing of Order statistics in 295
Prediction, distribution-free intervals 167Ч169
Prediction, parametric intervals 208Ч211
Prediction, point predictors 209Ч211
Princeton study 217Ч218
Probability plotting 270Ч273 284
Q-Q plotting 270
Quality control 274Ч277
Quantile, density function 84
Quantile, differences 163Ч164
Quantile, function 5
Quantile, population 5
Quantile, sample 5
Quantiles, asymptotic (joint) distribution of 285Ч290 316 347
Quantiles, bootstrap estimation of 183Ч185 227Ч228
Quantiles, bounds for  in terms of 80Ч83 in terms of 80Ч83
Quantiles, distribution-free confidence intervals for 159Ч164 169Ч170
Quasi-midrange 242
Quasi-range 15
Quasi-range in estimation of  248 364Ч365 248 364Ч365
Quasi-range in normal samples 248Ч249 326 351 364
Quasi-range, moments of 356
Quasi-range, tables of cdf 356
QuenouilleТs method see УJackknifeФ
Quick statistics 239Ч282 see
| Random division of an interval 133Ч137 153Ч155
Random division of an interval, distribution of longest interval 135 154Ч155 362
RANGE 1
Range for discrete parent 30 261Ч262
Range in quality control 274Ч276
Range in short-cut methods 239Ч240 243Ч247 257Ч262 356
Range in uniform distribution 175
Range ratios, 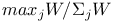 136 258 362 136 258 362
Range ratios,  365 365
Range ratios, in normal distribution 257 365
Range ratios, in uniform distribution 27 363
Range to spot gross errors 247Ч248
Range, applications of 239Ч240
Range, approximations to 244Ч246
Range, asymptotic distribution of 324Ч326
Range, bivariate (extreme spread) 251
Range, bounds for moments of 64Ч65
Range, distribution of 13Ч14 26Ч27
Range, effect of nonnormality on 245 247
Range, efficiency of 240 243 277
Range, mean 244
Range, moments of 37 54 356Ч357
Range, moving 140Ч141 276
Range, noncentral 280
Range, power function of range tests 254Ч256 279Ч280
Range, recurrence relations for expected 56Ч57
Range, studentized see УStudentized rangeФ
Range, tables relating to 356
Range, variance of 54
Range, УthickenedФ 248Ч249 259
Rank-order statistics 3
Ranked-set sampling 262Ч267 280Ч281
Rate of convergence of 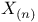 302Ч303 302Ч303
Rate of convergence of L-statistics 334Ч335
Ratio of Order statistics 28
Rayleigh distribution 204 359 364
Rayleigh distribution, optimal spacing of Order statistics in 295
Record values 20Ч21 32 87 307 328
Rectangular distribution see УUniform distributionФ
Recurrence relations between moments and cdfТs of Order statistics 23 44Ч49
Recurrence relations for Order statistics in non-iid variates 104Ч106
Regression coefficient, quick estimate of 251Ч252
Regression model, estimation of parameters in 202Ч203
Reliability 207Ч208
Robust estimation 211Ч223
Robust estimation in contaminated normal distribution 360
Robust estimation in presence of outliers 211 218Ч223
Robust estimation of mean of symmetric distributions 212Ч216
Robustness, lack of exponential in life testing 204
Robustness, lack of tests for homogeneity of variances 258
s-comparison 80 82Ч83
SCALE see also УLocation and scale parametersФ
Scale, estimation in presence of outliers 222Ч223
SchwarzТs inequality 61 86
Scores 33
Selection differential 41Ч42 53 65 102 351Ч353
Selection differential, induced 144 348 353
Selection procedures 102 144
Sensitivity curve 218
Sequential, confidence intervals 164
Sequential, tests based on range 258 260
Serial correlation 136
Series system 90
Short-cut procedures 239Ч282
Short-cut procedures by optimal spacing of Order statistics 290
Short-cut procedures for discrete variates 281Ч282
Short-cut procedures for estimating dispersion 243Ч248
Short-cut procedures for estimating location 241Ч243
Short-cut procedures for tests in normal samples 257Ч261 365
Short-cut procedures in bivariate samples 250Ч253
Short-cut procedures, tables for 365
Signal processing 141
Simulation, Order statistics in 15 355
Sorting (ordering) 31 355
Spacings (differences between successive Order statistics) 64 134Ч136 138 153Ч154 187Ч188 273
Spacings from exponential distribution 18 113 142
Spacings of order m 136Ч137 290 341Ч342
Spacings, asymptotic distributions 154 308 319Ч320 327Ч328
Stable distributions 295
Star-shaped 76
Stein's test, range version of 260
Stochastic orderings 74Ч80
Stratified samples 164
Structural inference 192
Student's distribution, moments of Order statistics in 359
Studentization 121Ч124
Studentization, external 121
Studentization, internal 121
Studentized range 1 121Ч124
Studentized range in analysis of variance 253Ч256
Studentized range in multiple comparisons 253Ч256
Studentized range, bounds for internally 247Ч248
Studentized range, noncentral 256 280
Studentized range, tables 360Ч362
Sufficient statistics, Order statistics as 172
Superadditive 76Ч77
Symmetric distributions 22 36 50
Symmetric distributions, bounds for moments of Order statistics in 62Ч64
Symmetric distributions, estimation of location and scale parameters in 179Ч180
Symmetric distributions, robust estimation of mean of 211Ч218
Symmetric distributions, tests for 274
Symmetric power distribution 215
Systematic statistics = function of the order statistics 15
Tables 4 355Ч366
Time series 135 140Ч141
Tolerance (= breakdown point) 215Ч216
Tolerance intervals for normal distributions using range 276Ч277 366
Tolerance intervals in exponential distribution 234
Tolerance intervals, distribution-free 164Ч167 169 363
Total time on test, statistic 91 209 234Ч235
Total time on test, transform 91
Trimmed mean 51 213
Trimmed mean as robust estimator 213Ч216
Trimmed mean in Cauchy distribution 237
Trimmed mean in normal distribution 242
Trimmed mean, asymptotic distribution of 329Ч331 335
Truncated distributions, moments of Order statistics in 359
Truncated normal distribution, estimation for 193Ч194
Truncation, estimation of parameters in case of 191Ч194
Truncation, versus censoring 191Ч192
TukeyТs  -distributions 63Ч64 -distributions 63Ч64
TukeyТs  -distributions in robustness studies 214 247 -distributions in robustness studies 214 247
UMP tests based on Order statistics 178Ч179
UMVU estimators, Order statistics as 174Ч175
Unbiased nearly best linear estimator 191
Uniform distribution 14Ч15
Uniform distribution, censoring in 230 233
Uniform distribution, differences of Order statistics in 14
Uniform distribution, estimation of parameters of 173Ч177 224
Uniform distribution, hypothesis testing in 177Ч179 363
Uniform distribution, L-statistics in 139
Uniform distribution, midpoint in 26Ч27
Uniform distribution, moments of Order statistics in 35Ч36 356
Uniform distribution, percentage points of Order statistics in 355
Uniform distribution, random division of interval 133Ч135
Uniform distribution, range in 356 363
Uniform distribution, range ratio in 27 178 363
Unimodal distribution of Order statistics 23
Upper percentage points, of statistics expressible as maxima 125Ч127 361Ч362 see
VandermondeТs theorem 129
Variance, analysis of see УAnalysis of varianceФ
Variances of Order statistics 34Ч35 see
Weibull distribution 364
Weibull distribution in asymptotic theory 284
Weibull distribution, estimation for 364
Weibull distribution, moments of Order statistics in 359
Weibull distribution, optimal spacing of Order statistics in 295
Weibull distribution, percentage points of Order statistics in 355
Whitworth 136
WilcoxonТs test, relation to robust estimation 215
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



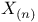 ,
,  ,
,  in multinomial
in multinomial  ,
,  , application of
, application of 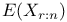
 and
and  for
for 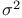
 in terms of
in terms of 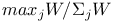

 -distributions
-distributions