|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Berndt B.C., Evans R.J., Williams K.S. Ч Gauss and Jacobi Sums |
|
|
 |
| ѕредметный указатель |
Abe, M. 387
Abel-Plana summation formula 51
Acharya, V.V. 98 152 209 211
Adleman, L. 97
Adolphson, A. 387
Agrawal, M.K. 99 210 232 292 497
Aigner, A. 99 231Ч232 267
Airy integral 386
Akiyama, S. 385Ч386
Aladov, N. 210
Alderson, H.P. 99 232
Andrews, G.E. 51 209 385
Ankeny, N.C. 99 232
Aoki, N. 336
Apery number 467
Apostol, T.M. 8 29 52
Artin's reciprocity law 494 495
Artin, E. 494
Askey, R. 385
Auslander, L. 52
Autocorrelation 439
Automorphism 26
Automorphism, Frobenius 387
Autuore, J. 385
Averbukh, I.SH. 3 54
Ayoub, R. 8 51
Babaev, G. 173
Bach, E. 339
Bachmann, P. 97 171 338
Bailey, D. 293
Bambah, R.P. 52
Barkan, P. 164
Barrucand, P. 50 231
Basse's conjecture 385
Baumert, L.D. 3 150 152 174 179 181Ч182 385 439
Beeger, N.G.W.H. 232 482
Bellman, R. 52
Benkoe, I. 51
Berndt 6
Berndt, B.C. 6 51Ч52 54Ч56 98 151 169 171Ч172 181 195 209 211 338 377 387 396 438Ч439 465Ч467 496Ч497
Berry, M.V. 3 54Ч55
Bessel function 386
Beukers 293
Beukers, F. 293
Beyer, G. 160
Bickmore, C.E. 231Ч233
Binomial coefficients 18 268
Binomial coefficients, Cauchy Ч Whiteman congruences for 292
Binomial coefficients, congruences (mod 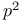 ) for 211 268 280Ч286290 293 498 ) for 211 268 280Ч286290 293 498
Binomial coefficients, congruences (mod p) for 200Ч202 211 268Ч274 288Ч292 417Ч419 435 437
Binomial coefficients, relationship with Jacob sums 66 268 279 6
Bochner, S. 52
Bombieri, E. 183
Borevich, Z. 53Ч54
Boyarsky, M. 388
Brauer, A. 210
Bremser, P.S. 55
Bressoud, D.M. 51
Brewer sum 5 440
Brewer sum, generalized 440 458 466
Brewer sum, generalized, 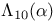 464 464 464 464
Brewer sum, generalized, 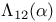 464 466 464 466
Brewer sum, generalized, 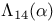 466 466
Brewer sum, generalized, 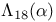 466 466
Brewer sum, generalized, 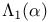 460 460
Brewer sum, generalized, 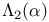 461 461
Brewer sum, generalized, 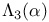 461 461
Brewer sum, generalized, 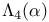 463 463
Brewer sum, generalized, 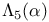 464Ч466 464Ч466
Brewer sum, generalized, 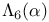 463 466 463 466
Brewer sum, generalized, 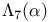 466 466
Brewer sum, generalized, 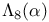 464 466 464 466
Brewer sum, generalized, 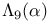 466 466
Brewer sum, generalized, 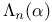 , , 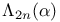 440 458Ч459 466 440 458Ч459 466
Brewer sum, generalized, relationship with Jacobsthal and Eisenstein sums 459
Brewer sum, ordinary 440 443 466
Brewer sum, ordinary, 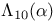 456 456
Brewer sum, ordinary, 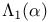 450 450
Brewer sum, ordinary, 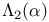 450 450
Brewer sum, ordinary, 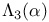 450Ч451 466 450Ч451 466
Brewer sum, ordinary, 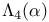 452 466 452 466
Brewer sum, ordinary, 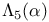 454 465Ч466 454 465Ч466
Brewer sum, ordinary, 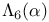 453 453
Brewer sum, ordinary, 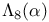 457 467 457 467
Brewer sum, ordinary, 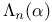 , , 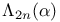 440 444Ч445 447 450 453 456 458 466 440 444Ч445 447 450 453 456 458 466
Brewer sum, ordinary, relationship with Jacobsthal and Eisenstein sums 445 450
Brewer, B.W. 3 5 53 211 440 466Ч467
Brillhart, J. 249
Brinkhuis, J. 384 387Ч388
Bruckner, H. 494
Bruedern, J. 340
Brumei Ч Stark element 495
Brumer Ч Stark conjecture 387
Buck, N. 152
Buell, D.A. 210 292
Burde, K. 209Ч211 232 266Ч267 498
Burgess, D.A. 5 55
Burnside, W. 338
Bushnell, C. 55
Caragiu, M. 210
Carey, F.S. 338
Carlitz 1
Carlitz, L. 1 51Ч52 54 336 340 384Ч387
Cassels, J.W.S. 158Ч160 494Ч495
Cauchy 1
Cauchy, A. 1 51 97 291Ч292
Cayley, A. 338
Chalk 6
Chalk, J.H.H. 6
Chandrasekharan, K. 52
CHARACTER 9 28
Character sum 28 58 173 183 198 206Ч208 210 385 387 400 449 453 467;
Character, biquadratic 241
Character, conductor of 28 45 380 387 495
Character, cubit 235
Character, Dinchlet 28 379
Character, Hecke 387 495
Character, k-power residue see УPower residue symbolФ
Character, lift of 342 356 385
Character, primitive 29 45 49Ч50 53Ч54
Character, quadratic 12 29 54 379 382
Character, quart it 241
Character, restriction of 355
Character, trivial 9
Chowla 1
Chowla Ч Mordell theorem 53
Chowla, I. 336
Chowla, P. 466
Chowla, S. 1Ч2 31 52Ч54 171Ч172 181 209Ч211 231 268 293 336 338 340 386
Chung, F.R.K. 387
Class number 54 164 377
Coates, J.H. 384
Code word 368Ч369;see also УWeightФ
Cohen, E. 337
Cohen, H. 97
Cohen, S.D. 98 174 211
Cohn, H. 231
Coleman, R.F. 350 3&8
Collison, M.J. 264
Congruences see also УDiagonal equationsФ
Congruences, Cauchy Ч Whiteman type 292
Congruences, Cauchy Ч Whiteman type, 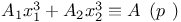 310 321 324Ч325 327 310 321 324Ч325 327
Congruences, Cauchy Ч Whiteman type, 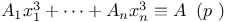 307 337 307 337
Congruences, Cauchy Ч Whiteman type,  317 321 333 337 317 321 333 337
Congruences, Cauchy Ч Whiteman type,  314Ч315 314Ч315
Congruences, Cauchy Ч Whiteman type, 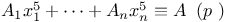 337 337
Congruences, Cauchy Ч Whiteman type, 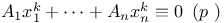 331 331
Congruences, Cauchy Ч Whiteman type, 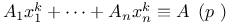 320Ч321 320Ч321
Congruences, Cauchy Ч Whiteman type, 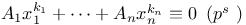 340 340
Congruences, Cauchy Ч Whiteman type, 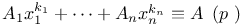 294Ч295 294Ч295
| Congruences, Cauchy Ч Whiteman type,  320Ч321 320Ч321
Congruences, Cauchy Ч Whiteman type, 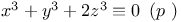 334 334
Congruences, Cauchy Ч Whiteman type, 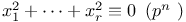 46 46
Congruences, Cauchy Ч Whiteman type, 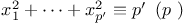 306 306
Congruences, Cauchy Ч Whiteman type, 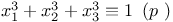 2 325 2 325
Congruences, Cauchy Ч Whiteman type, 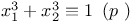 323 323
Congruences, Cauchy Ч Whiteman type, 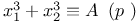 310 310
Congruences, Cauchy Ч Whiteman type, 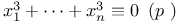 313 335 313 335
Congruences, Cauchy Ч Whiteman type, 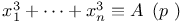 312 312
Congruences, Cauchy Ч Whiteman type, 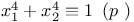 323 323
Congruences, Cauchy Ч Whiteman type, 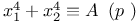 317 335 317 335
Congruences, Cauchy Ч Whiteman type, 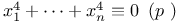 332 332
Congruences, Cauchy Ч Whiteman type, 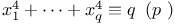 337 337
Congruences, Cauchy Ч Whiteman type, 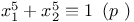 323 323
Congruences, Cauchy Ч Whiteman type, 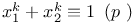 322 322
Congruences, Cauchy Ч Whiteman type, 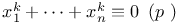 339 339
Congruences, Cauchy Ч Whiteman type, 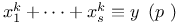 339 339
Conrad, K. 293 384
Continued fraction 164
Cooke, G. 265Ч266 494
Corson, H.H. 341
Coster, M.J. 293
Cowles, J. 338 340
Cowles, M. 338 340
Cox, D.A. 53 157 494Ч495
Crandall, R. 4 164 284 482
Cunningham 99
Cunningham, A. 99 231Ч232
Curtis, C.W. 385Ч386
Cyclic code 368
Cyclotomic field 26
Cyclotomic matrix 68
Cyclotomic matrix of older 8 95
Cyclotomic matrix of order 2 70
Cyclotomic matrix of order 3 70
Cyclotomic matrix of order 4 70
Cyclotomic matrix of order 5 93
Cyclotomic matrix of order 6 94
Cyclotomic matrix of order 7 95
Cyclotomic number 3 4 68 81 98Ч99 181Ч182 365
Cyclotomic number of of order 12 152
Cyclotomic number of of order 14 152
Cyclotomic number of of order 15 152
Cyclotomic number of of order 16 152 229
Cyclotomic number of of order 18 152
Cyclotomic number of of order 20 152
Cyclotomic number of of order 24 152
Cyclotomic number of of order 32 496
Cyclotomic number of order 10 152
Cyclotomic number of order 11 152
Cyclotomic number of order 2 69 80Ч81 152
Cyclotomic number of order 3 70Ч71 74 149 152
Cyclotomic number of order 4 70 74 78 149 152
Cyclotomic number of order 5 93Ч94 99 149 152
Cyclotomic number of order 6 94 149 152
Cyclotomic number of order 7 149 152
Cyclotomic number of order 8 149 152
Cyclotomic number of order 9 152
Cyclotomic number relationship with f-normal periods 328Ч329 437Ч438
Cyclotomic number relationship with Jacobi sums 79 95 98 365
Cyclotomic number, generalized 87 322
Cyclotomic period see УPeriod f-normalФ
Cyclotomic polynomial 62
Dabrowski, R. 387
Dantscher, V. 265
Darmon, H. 338
Davenport 1
Davenport Ч Haase product formula 4 59 342 351 355 384Ч386 497
Davenport Ч Hasse theorem on lifted Gauss sums 4 342 358 360 392 492
Davenport, H. 1 4 50Ч51 53 209Ч210 384Ч385
Davis, K. 293
Desarmenien, J. 293
Deuring's theorem 210
Deuring, M. 210
Diagonal equations 3Ч4 294 336 340;
Diagonal equations,  338 338
Diagonal equations, 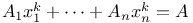 340 437 340 437
Diagonal equations, 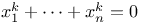 340 340
Diagonal equations, 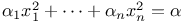 305 305
Diagonal equations, 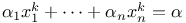 394 303Ч304 319Ч320 339Ч340 394 303Ч304 319Ч320 339Ч340
Diagonal equations, 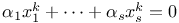 340 340
Diagonal equations, system of 340Ч341
Diamond, H.G. 55 241
Dickson polynomial 386 440 443
Dickson's Diophantine system for p=5f+1 94 131 151
Dickson's Diophantine system for p=5f+1, analogue for p=7f+1 143
Dickson, L.E. 5 97 131Ч132 150Ч152 336Ч338 384
Dieudonne, J. 56
Difference set 174 181Ч182
Difference set, Abelian 174
Difference set, cyclic 174
Difference set, modified power residue 174 497
Difference set, planar 174
Difference set, power res due 174Ч175 181 497
Difference set, supplementary 181
Dilcher, K. 4 164 284 482
Dimitrakoudis, D. 55
Dirichlet 1 54
Dirichlet character 26 379
Dirichlet's class number formula 54 377
Dirichlet's L-function 54; see also УL-functionФ
Dirichlet, G.L. 1 51 53Ч54 99 231 264
Discrete Fourier Transform 47 01Ч52
Discriminant of period polynomial 155Ч339
Disquisitiones Arithmeticae 1 97
Doerge, K. 210
Drmota, M. 3 172
Du, D.Z. 99
Duke, W. 386
Dunton, M. 338
Dwork, B. 2 211 268 293
Eichler, M. 52
Eigenspace 51
Eigenvalue 47Ч48 51
Eigenvector 51
Eisensrein prime 234
Eisenstein 1
Eisenstein integer 234
Eisenstein integer primary 236
Eisenstein integer prime 234
Eisenstein sum 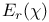 389Ч400 438 389Ч400 438
Eisenstein sum 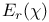 (over (over 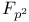 ) 396Ч399 438 ) 396Ч399 438
Eisenstein sum 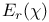 , congruence for 394 414Ч415 419 , congruence for 394 414Ч415 419
Eisenstein sum 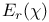 , of order 10 435 , of order 10 435
Eisenstein sum 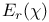 , of order 12 433 , of order 12 433
Eisenstein sum 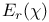 , of order 16 430 , of order 16 430
Eisenstein sum 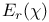 , of order 2 393 , of order 2 393
Eisenstein sum 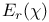 , of order 20 428 , of order 20 428
Eisenstein sum 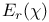 , of order 24 435Ч436 , of order 24 435Ч436
Eisenstein sum 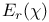 , of order 3 400Ч101 435 , of order 3 400Ч101 435
Eisenstein sum 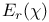 , of order 4 402 435 , of order 4 402 435
Eisenstein sum 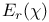 , of order 5 403Ч404 , of order 5 403Ч404
Eisenstein sum 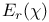 , Of order 6 405Ч406 , Of order 6 405Ч406
Eisenstein sum 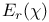 , of order 7 412Ч413 416 , of order 7 412Ч413 416
Eisenstein sum 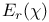 , of order 8 407Ч406 416 , of order 8 407Ч406 416
Eisenstein sum 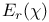 , order of 390 , order of 390
Eisenstein sum 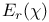 , relationship with Gauss sums 391 393 421 , relationship with Gauss sums 391 393 421
Eisenstein's congruences for binomial coefficients 5 414 417Ч419
Eisenstein's reciprocity law 5 234 267 468 474 494
Eisenstein's reciprocity law for Gauss sums 493Ч495
Eisenstein, G. 1Ч5 53 97 264Ч266 336 338 438 468 494
Elliptic curves 210Ч211 266 387 466
Equations see УDiagonal equationsФ
Error correcting code 369 371
Estenuann, T. 24 52 386
Estermaun's evaluation of a quadratic Gauss sum 24
Euclidean Domain 240 250
Euler, L. 231
Evans 6
Evans, R.J. 2 4Ч5 51 53 55Ч56 63 98Ч99 151Ч152 171Ч173 181Ч182 195 209 211 229 232Ч233 267Ч268 293 338Ч339 385Ч388 396 400 438Ч439 453 465Ч467 494 497Ч498
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



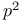 ) for
) for 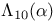
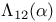
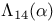
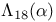
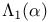
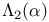
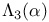
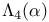
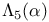
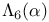
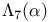
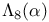
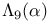
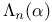 ,
, 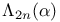



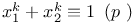
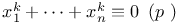
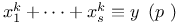

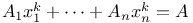
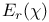
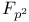 )
)