|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bachman G. — Introduction to p-Adic Numbers and Valuation Theory |
|
|
 |
| Предметный указатель |
Absolute convergence 98
Adeles 167
Algebraic closure 166
Algebraic integer 89
Analyticity 114
Approximation theorem 21
Archimedian ordered group 78
Associated place 69
Associated valuation 74
Associated valuation ring 68 73
Banach algebra 111
Banach space 94
Binomial series 51
Bounded linear functional 100
Canonical homomorphism 160 163
Cauchy sequence 16 94
Characteristic 164
Chinese remainder theorem 22 136
Commutative normed algebra 111
Complete field 24
Complete residue system 156
Completion of a field 26—33
Congruence 26
Conjugate embeddings 130
Convergence, absolute 98
Convergence, p-adic valuation 4
Convergence, rank one valuation 24
Convex functional 103
Degree of separability 166
Degree, extension 165
Discrete valuation 143
Discriminant 142
Divisibility 164
Domain of convergence 43
Double coset 161
Eisenstein criteria 151
Equivalent norms 94
Equivalent places 70
Equivalent valuations 16
Euclidean Domain 165
Euler  -function 156 -function 156
Euler theorem 156
Exponential series 46 47
Extension of a valuation, archimedian 126—128
Extension of a valuation, non-archimedian 117—126
Extension, algebraic 165
Extension, field 165
Extension, finite 165
Extension, normal 165
Extension, separable 165
Extension, theorem 83—88
Extension, transcendental 165
Fermat's theorem 156
Fully ramified extension 152
Gelfand theorem 116
Global degree 132—133
Global norm 136
Global trace 136
Greatest common divisor (g.c.d.) 155—156
Group of units 23 67
Group, Galois 166
Group, ordered 70
Hahn — Banach theorem 103 106 107
Ideal 163
Ideles 168
Identity element 111
Induced valuation 130
Inductively ordered 155
Integral closure 89
Integral element 88
Irreducible element 164
Isolated subgroup 77
Isometry 26
| Kernel 161
Lagrange's theorem 159
Least common multiple 156
Legendre symbol 157
Linear functional 99 100
Linear functional, norm of 101
Liouville's theorem 114
Local degree 133
Local norm 136
Local trace 136
Logarithmic series 48 49
Metric 3 4 15 93
Metric spaces 3 4 15 93
Neighborhood (spherical) 15
Newton's method 52—57
Non-units 65
Norm 92 166
Normalized p-adic valuation 23
Normed algebra 111
Normed linear space 92
Null sequence 16
Order isomorphism 78
Ordered group 70 77
Ordinal 45
p-Adic integer 37
p-adic numbers 33 34
p-adic numbers (canonical expansion of) 35
p-adic valuation 2
Place 67—70
Power series in 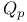 43 43
Prime 164
Prime field 164
Principal ideal domain 165
Quadratic non-residue 157
Quadratic reciprocity law 158
Quadratic residue 157
Radius of convergence (power series) 43 98
Ramification index 121
Rank of a valuation 77
Rank of an ordered group 77
Regular point 113
Relatively prime 156
Residue, class degree 121
Residue, class field 9 67
Residue, classes 156
Roots of unity in 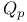 61 61
Semigroup 158
Spectrum 113
Splitting field 166
Subgroup 158
Subgroup, normal 160
Sublinear functional 103
Symmetric convex functional 107
Trace 167
Trivial valuation ring 65
Ultra-metric inequality 3 4
Unique factorization domain 165
UNIT 162
Units, Group of 23 67
Valuation of algebraic number field 137
Valuation of rank one 5
Valuation, associated 74
Valuation, discrete 143
Valuation, equivalent 16 75
Valuation, general 72
Valuation, induced by an embedding 130
Valuation, non-archimedian 5 72
Valuation, normalized p-adic 23
Valuation, p-adic 2 5
Valuation, ring 9 65
Valuation, trivial 9
Valuation, vector 168
Zorn's lemma 155
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -function
-function