|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Alexandroff P. — Elementary Concepts of Topology |
|
|
 |
| Предметный указатель |
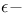 covering 35 covering 35
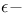 transformation 47 transformation 47
Abstract geometrical complex 40
Alexander's duality theorem 53
Alexander's theorem on invariance of Betti groups 32
Algebraic complex 12 17 18
Algebraic complex with arbitrary coefficient domain 29 (n.25)
Algebraic complex, subdivision of 29
Algebraic subcomplex 18
Algebraic topology 12 17
Approximating complex 41
Approximation, simplicial 46
Barycenter 37
Barycentric covering 36
Barycentric star 38
Barycentric subdivision 37
Betti groups 26
Betti groups free 26
Betti groups full 26
Betti groups reduced 26
Betti groups, invariance theorem for 32
Betti number 26
Boundary 12
Boundary divisor 23
Bounding cycle 22
Brouwer dimension 36
Brouwer's theorem on invariance of dimension 31
Canonical displacement 43
Canonical displacement modified 43
Center (of barycentric star) 38
Class, homology 24
Closed manifold 7 10
Coefficient domain 29 (n.25)
Combinatorial topology 12
Complex oriented 14
Complex, abstract geometrical 40
Complex, algebraic 12 17 18
Complex, geometrical 6
Complex, n-dimensional 28
Component 26 (n.22)
Connected 7
Consistently oriented 18
Continuous mapping 9
Covering, barycentric 36
Covering, barycentric,  35 35
Curve, Jordan 2
Curve, simple closed 2
Curved polyhedron 7
Curved simplex 7
CYCLE 20
Cycle bounding 22
Dimension general 36
Dimension of frame 40
Dimension, Brouwer 36
Dimension, Brouwer's theorem on invariance of 31
Displacement, canonical 43
Displacement, modified canonical 43
Divisors, boundary 23
Domain vertex 40
Domain, coefficient 29 (n.25)
Duality theorem, Alexander's 53
Duality theorem, Poincare's 52
Equivalently oriented 18
Face (of simplex) 6
Face (of simplex) abstract 40
Fineness 46
Frame 40
Frame, dimension of 40
Frame, simplex spanned by 40
Free Betti group 26
Full Betti group 26
Geometrical complex 6
Geometrical complex abstract 40
Geometrical complex, algebraic subcomplex of 18
Geometrical complex, subdivision of 29
Group homology see Betti groups
Group torsion 26 (n 21) 51
Group, Betti 26
Hausdorff axioms 9
| Hausdorff space 9
Homeomorphic 21
Homeomorphism 21 (n 6)
Homologous 23
Homology class 24
Homology group see Betti groups
Homology, strong 23
Homology, weak 23
Homomorphism, induced 46
Induced homomorphism 46
INTO 33 (n 31)
Invariance of Betti groups, Alexander's theorem on 32
Invariance of dimension, Brouwer's theorem on 31
Invariance theorem, topological 31
Invariant, topological 6—7 (n 6)
Jordan arc, simple 4
Jordan curve 2
Jordan curve theorem 2
Jordan curve theorem generalized 2 3
Leading vertex 37
Lebesgue number 42
Lebesgue's lemma 42
Linked 2
Manifold, closed 7 10
Manifold, product 10
Mapping, continuous 9
Mapping, simplicial 32—33
Mapping, topological 7
Modified canonical displacement 43
Modulo 2 theory 27
Modulo m theory 29 (n 25)
n-dimensional complex 28
Neighborhood 7 9
Nerve 39
Onentable 17 20
Onto 33 (n 31)
Order (of a covering) 35 (n 37)
Oriented complex 14
Oriented simplex 12 17
Oriented, consistently 18
Oriented, equivalently 18
Poincare's duality theorem 52
Polyhedron 6
Polyhedron, curved 7
Projection spectrum 41
Projective plane 8
Reduced Betti group 26
Simphcial approximation 46
Simphcial mapping 32—33
Simple closed curve 2
Simple Jordan arc 4
simplex 6
Simplex curved 7
Simplex oriented 12 17
Simplex spanned by frame 30
Simplex, face of 6
Space, Hausdorff 9
Space, Hausdorff, product 10
Space, Hausdorff, topological 8
Spectrum, projection 41
Star, barycentric 38
Strong homology 23
Subcomplex of algebraic complex 29
Subcomplex of geometric complex 29
Subcomplex, algebraic 18
Tiling theorem 1
Tiling theorem, proof of 35-36
Tnangulation 13
Topological invariance theorem 31
Topological invariant 6—7 (n 6)
Topological mapping 7 (n 6)
Topological space 8
Topology, algebraic 12 27
Topology, combinatorial 12
Torsion group 26 (n 21) 51
Transformation,  47 47
Vertex domain 40
Vertex leading 37
Vertex, abstract 40
Weak homology 13
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 covering
covering