Авторизация
Поиск по указателям
Conway J.H. — The Book of Numbers
Обсудите книгу на научном форуме Нашли опечатку?
Название: The Book of NumbersАвтор: Conway J.H. Аннотация: In this book, John Horton Conway, creator of the famous game of Life, and one of the most original thinkers in mathematics, joins up with Richard K. Guy, whose broad understanding of the subject is often dressed up in playful expository language. Together they lead the reader on an imaginative, often astonishing tour of the landscape of numbers.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1998Количество страниц: 310Добавлена в каталог: 07.12.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
65 93 258-259 see Arithmetic modulo Ackermann numbers 60 Adams,J. F. 235 Addition of nimbers 293 Addition, associative law of 216 Addition, by geometry 215 Addition, in Hackenbush game 287 Additive pattern 74 Aleph zero ( 25 278 Algebra, geometry and 27-62 Algebra, shuffles and 167 Algebraic equations 194 Algebraic equations for girls and boys 205-206 Algebraic numbers 23 189-190 Algebraic numbers of degree three 190-191 Algebraic numbers of degree two 190 Algebraic numbers, geometry and 181-210 Algebraic numbers, in arithmetic problems 202-205 Angle(s) 195-197 Angle(s), bisectors of 199 202 Angle(s), neusis trisection of 195 Angle(s), trisectors of 198-199 Apery’s number 261-262 Arabic number system 18 Arabic number system, 20-21 Archimedean solids 53 Archimedes and pi ( 238 Archimedes, neusis trisection of angle 195 Arithmetic, geometry and 27-62 Arithmetic, geometry and, modulo 130-132 Arithmetic, geometry and, problems, algebraic numbers in 202-205 Arithmetic, geometry and, progression 35-38 Arrangement numbers 66 arrow notation 60 Artin, Emil 170 Associative law of addition 216 Associative law of addition of multiplication 216 Astronomy 17-18 175 Axiom of Choice 274-275 Axis 199 Babylonian cuneiform 173-174 181-182 Babylonian cuneiform, numerals 17 20-21 Baker, Alan 224 Bases, numbers in 21 Bell numbers 91-93 Bell, Eric Temple 91 Berlekamp, Elwyn 288 Bernoulli numbers 107-109 Bernoulli, Jacob (James) 107 Bifurcating trees 98 Bifurcation points 208 Billion, use of term 13-16 Binary numbers 21 Binary trees 98 Binary trees, exponentiations and 103 Binomial theorem 43 73 Bisectors 199 202 Bouton, C.L. 291 Brent, Richard 139 Brillhart, John 139 Brown, J. 136 Buds see Phyllotaxis Bushes Buds, exponentials and 103 Buds, mountains and 104 Calabi, Eugenio 206 Calabi’s triangle 206 calendar 175 Cantor, Georg 25 (see also Cardinal numbers; Ordinal numbers) Cantor, Georg and aleph zero ( 25 Cantor, Georg and cardinal numbers 25 Cantor, Georg, counting cards and 279-282 Cantor, Georg, infinite numbers and 25 Cantor, Georg, ordinal numbers of 25 266-271 275-276 Cardinal numbers 25 277-279 Cardinal numbers, counting cards and 279-282 Cardinal numbers, first infinite ( 278 cards see Shuffles Carmichael numbers 142 Casting out the nines 28-29 Catalan numbers 101 Catalan numbers, mountains and 105-106 Cayley numbers 234-235 Cayley, Arthur 234 Centred cube numbers 52 Centred square numbers 41 42 Chain, Hackenbush 286 287 289 Choice numbers 67-68 Choice numbers with repetitions 70 Choice numbers, as binomial coefficients 72-74 Chuquet, N. 13 14 Circle, degrees of 17 Circle, squaring of 191 Classes, ordinal and cardinal numbers in 277-278 Clausen 109 Coefficients 72 Cohen, Paul 282 Colors, patterns and 29-30 Combinations 67 Comma of Pythagoras 257 Compass, Euclid and 191-192 complex numbers 23 214 Composite numbers 127 Compositions 95 Computers, very large numbers and 59-60 Congruence, “casting out the nines” and 28-29 Congruent modulo 28 Congruent to 1 Congruent to, modulo 3 28 Constructions, of Euclid 191-192 Continued fractions 175-179 Continued fractions, harmony, logarithms, and 257 Continuum Hypothesis 282 Convergents 178 Countable set 278-279 Counting 275-276 (see also Ordinal numbers of same set in different ways) Counting cards 279-282 Counting numbers 69 Counting, from zero 265-266 Cube numbers, centred 52 Cubes 42 Cubes, Sums of 57-58 Cubes, tesseracts as 55 Cubes, very large numbers and 59 Cuneiform script 17 173 174 181-182 Cycle, Metonic 175 De divina proportione (Pacioli) 184 De la Roche, Emile 14 De la Vall 260 De Moivre numbers 227 228 De Moivre numbers, circle cutting 226-228 De Moivre numbers, seventeenth-order 229 De Moivre, Abraham 226 Decimal system 21 Decimals, fractions and 157-163 Degree(s) algebraic numbers and 189 Degree(s) algebraic numbers and of circle 17 Delian number ( 193-194 Denominator 151 Denominator of fractions 157-160 Diaconis, Persi 165 Difference table 80 (see also Patterns;Sequences) Differencing, sequences and 79-81 Dimensions fourth 55-59 Dimensions fourth, third 42-44 Diogenes 255 Diophantus of Alexandria 172 Dirichlet, G.I. 260 Distance 3 296 297 Division, by geometry 215 Dubois - Raymond, Paul 299 Dubois - Raymond, Paul, 251 254 Egyptian number system 18 19-20 Eighty, words for 12 Eisenstein integers & units 205 220-221 222 223 Elements of Geometry, The (Euclid) 132 Empty set 266 Equations, algebraic 194 Equations, linear 192 Equations, Pell 204 Equations, quadratic 192 Equilateral triangle 206 Eratosthenes 127-128 Euclid, Mersenne primes and 137 Euclid, number theory and 132-133 Euclid, perfect numbers and 139 Euclid, ruler and compass constructions 191-192 Euclidean numbers 192-193 Euler - Maclaurin sum formula 260-261 Euler - Mascheroni number 17 25 260 Euler numbers 110-111 Euler, Leonard 137 Euler, Leonard, prime numbers and 225 Euler, Leonard, torient numbers of 154-156 167 198 Euler, Leonard, transcendental numbers and 253 254-256 Eulerian number, 111 Euler’s formula, for partition numbers 95 Even numbers 27 Exponentials, bushes and 103 Exponentiations, trees and 103 Exponents, laddered 98-100 Factor Table for the First Ten Million (Lehmer) 129-130 Factorial 65 Factorial numbers 64 65-66 Factors, prime 132-133 Families, of numbers 91 126 Farey series 152-154 156 Faulhaber’s formula 106 (see also Bernoulli numbers) Faulliaber, Johann 106 Fermat numbers 137-141 Fermat, Pierre de 138 Fermat, Pierre de, Little Theorem of 09 164 Fermat, Pierre de, prime numbers and 220 Fermat, Pierre de, prime of 197 Fermat, Pierre de, sum of two squares theorem 221 Fermat, Pierre de, test for primes 141-143 Fibonacci numbers 85 111-113 202-203 Fifth (interval) 256 Finite set 278 flowers see Phyllotaxis Ford, Lester R., Farey series and 153-154 Ford, Lester R., “Four,” use of word 8 Four-square formula 232 Fourth dimension 55-59 Fractions 23 151-179 Fractions and gear trains 178 179 Fractions for irrational numbers 186 Fractions modulo p 130-132 Fractions, as rational numbers 151 183 Fractions, babylonian table of Pythagorean 173 174 Fractions, continued 175-179 Fractions, decimals and 157-163 Fractions, harmony, logarithms, and 256-257 Fractions, long primes and 169-171 Fractions, prime numbers and 147-148 Fractions, Pythagorean 171-173 Fractions, Roman 22 23 Fractions, shuffling and 163-168 Fractions, Wilson’s theorem and 168-169 Freiman, G. A. 188 Freiman’s number 188 Frequency, of prime numbers 143 Frieze patterns 74-76 96-97 Frieze patterns, polygons and 101 Games, Hackenbush 284-291 (see also Green Hackenbush; Neutral Hackenbush) Games, Nim 291-298 Gardner, Martin 41 225-226 Gauss, Carl Friedrich 11 28 Gauss, prime and 139-140 144 146 Gauss, regular polygon and 193 Gaussian integers 217-223 Gauss’s numbers 244-245 Gear trains, fractions and 178 179 Generalized Continuum Hypothesis 282 Geometry and algebraic numbers 181-210 Geometry of physics 213 Geometry, adding and multiplying by 215 Geometry, arithmetic and algebra figured with 27-62 Geometry, polygons and 198-202 Gnomon 32 42 Gnomon and sums of cubes 57-58 Gnomon, bending nexus numbers and 55 Gnomon, defined 33 Godel, Kurt 282 Golden number (t) 25 112 123 184 Golden rectangle 184 Golden rule, for fractions 151 Graham, Ron, hexagon of 206-207 Graham’s number 61-62 Greece, algebraic numbers and 190-191 Greek number system 18 Green Hackenbush 297 Gregory numbers 241-243 244-245 246 247 Gregory, David 242 Hackenbush game 284-291 Hackenbush game, Green Hackenbush 297 Hackenbush game, Neutral Hackenbush 291-292 297 298 Hadamard, Jacques 143-144 Hamilton, William Rowan 231 234 Handshakes without crossing 100 Handshakes without crossing, parentheses and 104 Hardy G.H. 95 Harmonic numbers 143 258-259 Harmony, fractions, logarithms, and 256-257 Harmony, fractions, logarithms, and, words 12-13 Heegner 224 225 Heilbronn, H.A. 224 Heptadecagon 229-230 Hex numbers 41 Hex pyramids, as cubes 43 Hexadecimal system 21 Hexagon, folding 185 Hexagon, Graham’s 206-207 Hexagonal number 39 Hindu - Arabic number system 18 20-21 Hundred, words for 12-13 Hurwitz, A. 235 Hypercomplex numbers 230-232 imaginary numbers 211-214 In shuffle 163 164 Incommensurable numbers 213 Infinite and infinitesimal numbers 25 265-299 Infinite and infinitesimal numbers, Cantor’s ordinal numbers 266-271 275-276 Infinite and infinitesimal numbers, counting cards and 279-282 Infinite and infinitesimal numbers, Hackenbush game and 284-291 Infinite and infinitesimal numbers, multiplying ordinal numbers 271-276 Infinite and infinitesimal numbers, nimbers and game of Nim 291-298 Infinite and infinitesimal numbers, orders of infinity 299 Infinite and infinitesimal numbers, Sierpi 265-266 Infinite and infinitesimal numbers, surreal numbers and 283-284 Infinitesimal numbers see Infinite and infinitesimal numbers Infinity, orders of 299 Information sources, on number sequences 89 Integers, gaussian 217-223 Integers, unique factorization into primes 223 Integral lexicographic code 296 Internet, number checker on 26 Inverse Symbolic Calculator 25 26
Реклама
 |
|
О проекте
|
|
О проекте



 factorial
factorial 
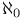 )
)  )
)  e Poussin, Ch. - J.
e Poussin, Ch. - J. ![$\sqrt[3]{2})$](/math_tex/4aca920eb07fb122fb8d9cfeef3e85c282.gif)
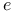 , powers of
, powers of 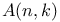
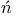 ski and
ski and