|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Chung K.L., Walsh J.B — Markov Processes, Brownian Motion, and Time Symmetry |
|
|
 |
| Предметный указатель |
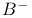 355 355
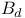 254 254
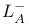 377 377
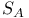 240 357 361 377 385 240 357 361 377 385
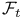 , , 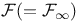 16 75 16 75
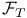 , , 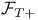 14 14
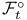 , , 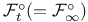 , , 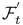 2 2
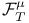 61 61
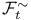 , , 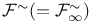 62 62
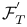 57 57
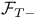 16 16
 250 250
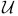 -compactification 274 275 277 287 289 -compactification 274 275 277 287 289
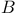 401 401
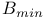 403 403
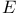 1 1
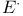 96 96
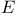 63 63
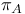 237 237
Absorbing state 9
Additive functional 199
Almost sure(ly) 26 51
Analytic set 40
Approximation of entrance and hitting times 93 94 113
Area of sphere 150
Augmentation 29 59
Austin, D. 302
Balayage 98 375
Barrier 179
Birth time 337
Blumenthal's zero-or-one law 64
Borel measurable process 18
Borelian semigroup 46
Boundary point 246
Boundary value problem for Laplace equation see under "Dirichlet problem"
Boundary value problem for Schroedinger equation 204
Branching measure 355
Branching point 246 254 259 280 321 348 355
Branching point, degenerate 254 274
Branching point, fork 255
Brownian motion 11 118 125 128 144ff 228 247 410
Brownian motion, continuity of paths 78
Brownian motion, killed outside a domain 177
Brownian motion, polarity of singleton 118 169
Brownian motion, potential density 128 129
Brownian motion, recurrence, transience 145
Brownian motion, rotational symmetry 149
Brownian motion, stopped 188
Brownian motion, transition density 144
Canonical space 321 324
Capacitable 388
Capacity 223 228 394
Capacity, Choquet 396
Cartan's theorem 116
Choquet's capacibility theorem 91
Choquet, G. 415
Chung, K.L. 298 302 415
Co-branching point 348
Co-capacity 394
Co-excessive 344 363
Co-left-regular 364
Co-optional 330
Co-polar 361 389
Co-potential 369
Co-semi-polar 361
Co-terminal time 338 360
Co-terminal time, associated 339
Cofine, component 370
Cofine, continuity 391
Cofine, topology 390
Compactification 248
Compatible 281
Cone condition 165
Continuity of paths 77
Continuity principle 231
Continuity, cofine 391 392
Continuity, fine 370 390 391
Convolution semigroup 137
Death time 337
Debut 40
Debut after t 267
Dellacherie's theorem 113
Dirichlet problem 166 286 287 411
Dirichlet problem for unbounded domain 170
Dirichlet problem, generalized 170 186
Dirichlet problem, unsolvable 167
Divergence formula 157
Domination principle 100
Doob — Meyer decomposition 48
Doob's continuity theorem 184 189
Doob's stopping theorem 30
Doob, J.L. 243 302 334 414
Double reversal 337 339
Dual process 139
Dual transition function 309
Duality 344 347
Duality formula 140
Duality, weak 344
Dynkin's lemma 4
Electrostatics 229 377
Energy 224
Energy minimization 226 230
Energy minimization principle 225
Entrance law 265
Equilibrium measure 213 3
Equilibrium measure, as steady state 227
Equilibrium potential 384
Equilibrium principle 218
Essential, inf 233
Essential, limit 233 242 271 293 294 311 312
Essential, limit point 296
Essential, separability 235 266
Essential, sup 233
Essential, topology 233 242
Exact 339
Excessive function 45 85
Excessive function, as limit of potentials 82 85 86
Excessive function, balayage properties 100
Excessive function, closure properties 81 104
Excessive function, decreasing limit 116ff
Excessive function, fine continuity 108
Excessive function, infinity of 104
Excessive function, purely 121
Excessive function, right continuity on paths 101
Excessive, measure 349 350
Excessive, minimal 327 330 331
Excessive, regular 386 391
Excursion 153
Feller process 50 289
Feller property 49 251 261
Feller — McKean diffusion 300
Feller, W. 248
Feynman — Kac functional 199
Filtration, continuity 259
Fine closure 97
Fine component 370 376
Fine continuity 370 390 391
Fine limit 413
Fine neighborhood 413
Fine recurrence 416
Fine symmetry 388
Fine topology 107 390
Fine transience 416
First blow-up 245
First entrance time 22
First entrance time, optionality, approximation see "Hitting time"
First infinity 245
Fork 255 279
Frostman 230
Functional, additive 358
| Functional, multiplicative 358
Gauge 205
Gauss formulas 157 162
Gauss formulas, quadratic 232
Gauss — Koebe theorem 156
Generalized Dirichlet problem 186
Getoor, R. 341
Ghostly return 298
Green's function 410
Green's function, potential 181
Green's function, potential for an interval 199
h-excessive 322 323 328 332 377
h-excessive measure 366
h-polar 332
h-thin 329 330
h-transform 325 331 332 334 348 364 365 367 376 378 396
h-transform, semigroup 321
Harmonic function 156ff 287 379 412
Harmonic function and martingale 182
Harmonic measure 162 412
Harnack's theorems 158
Harnack's theorems, inequality 200
Hitting probabilities for spheres 168 169
Hitting time 70
Hitting time, approximation 93 94 113
Hitting time, optionality 71 92
Hoelder condition 162
Holding point 79
Holes 342
Homogeneity 6
Homogeneity, spatial 137
Hunt process 75ff 244 245 258 276 277 288
Hunt's Lemma 238 280 313
Hunt's switching formula 219
Hunt, G.A. 384 397 414
Hypothesis (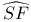 ) 371 374 375 378 386 387 389 391 ) 371 374 375 378 386 387 389 391
Hypothesis (B) 131 212 357 378 385—387 396
Hypothesis (L) 112 347 354 361 385 416 419
Hypothesis (MMP) 272 273 280
Hypothesis (MP) 269 270
Hypothesis (SF) 389 391
Hypothesis (SMP) 272 273 280
Hypothesis (UH) 274
Independent increments 142
inf-stable 269
Initial distribution 7
Instantaneous state 56
Invariant field 327 408
Invariant function 121
Invariant function, measure 138
Jacobsen, M. 341
Jump chain 245
Kellogg — Evans theorem 185 223
Kernel 6
Killing 279
Killing operator 353
Knight's Lemma 270 290
Knight, F. 268 290
Kolmogorov's extension theorem 6
Kunita, H. 290 397 414
Laplace equation 156
Laplace equation, radial solution 159
Laplacian, as infinitesimal generator 190 198
Laplacian, as inverse to potential operator 192 194
Last exit 329 394
Last exit time 121 209
Lazy crotch 286 289
Lcrl 272
Left co-polar 361
Left continuity 240
Left entrance, hitting time 95 134
Left polar 361
Left quitting time 213
Left-branching point 355
Left-regular 279 361
Levy process 137
Lifetime 9 371
Logarithmic potential 193
Markov chain 10 244 291
Markov process 2
Martin, boundary 347 401 410 414
Martin, compactification 409
Martin, kernel 399 401 410
Martin, R.S. 398 414
Martin, representation 404 406
Martin, space 399 401 410
Martingale 24 259
Martingale for Brownian motion 147 153
Maximum principle 394 see
Maximum principle for harmonic function 158
Maximum principle, Maria — Frostman 221
McKean, H.P. 300
Measurability questions 63
Meyer's theorem 32
Meyer, P.A. 251 341 415
Minimal chain 245
Minimal function 327 328 403 411
Minimal point 403 410
Moderate Markov property 69 256 298 303 354
Mokobodzki, G. 318 356 415
Monotone class 4
Near symmetry 393
Nearly Borel 95
Nearly equivalent 391
Occupation time 109
OPTIONAL 12
Optional field 43
Optionality of entrance and hitting times 71 92
p-potential 369
Penetration time 237 284 293
Penetration time, other 361
Perfect 339
Picard's theorem 161
Pitman, J.W. 341
Pittenger, A.O. 341
Point at infinity 9 48
Poisson equation 193 194 196
Poisson equation, formula 169
Poisson equation, integral 180
Poisson equation, process 11
polar 110 389
Polarity principle 222
Pole 330
Positivity principle 230
Potential 46 266 375 380 384
Potential, lower semi-continuity 126
Predictable 17
Predictable field 43
Predictable time 258 289
Process, Hunt 75 244 245 258 276 277 288
Process, moderate Markov 251 255 258 273 304 354—356 365 418
Process, Poisson 11
Process, Ray 258—260 263 266 268 270 274 276 303
Process, standard 246 277 288
Process, strong Markov 255 256 268 272 273 365
Progressive measurabilify 37
Projection theorem 40
Q-matrix 244
Quasi left continuity 70
Quasi-left continuity 264 356 357 362 385—387 396
Quitting kernel 209 212 213
Quitting time 121 209 213
Radon measure 212
Ray process 258 260 263 266 268 270 274 276 293 303
Ray resolvent 251 270 303
Ray — Knight compactification 268 272 286 291 292 301 303 337 409
Ray, D. 251 290
rcll 272
Recurrent process 122
Recurrent process, set 121
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



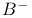
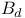
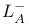
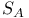
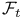 ,
, 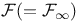
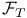 ,
, 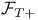
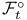 ,
, 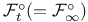 ,
, 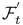
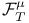
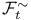 ,
, 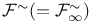
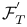
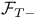

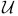 -compactification
-compactification 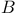
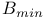
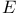
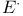
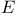
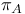
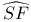 )
)