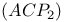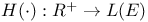|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Xiao T.-J., Liang J. — Cauchy Problem for Higher Order Abstract Differential Equations |
|
|
 |
| Предметный указатель |
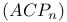 Preface Preface
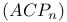 , analytically solvable in , analytically solvable in 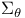 4.1 4.1
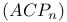 , entire solution 4.4 , entire solution 4.4
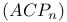 , propagator 2.1 , propagator 2.1
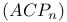 , solution 2.1 , solution 2.1
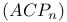 , solvability 2.3 , solvability 2.3
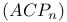 , strong C-propagation family 3.5 , strong C-propagation family 3.5
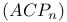 , strongly C-wellposed 3.5 , strongly C-wellposed 3.5
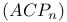 , strongly wellposed 2.1 , strongly wellposed 2.1
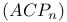 , wellposed 2.1 , wellposed 2.1
![$(ACP_{n})_{[B_{n-1}, \ldots, B_{0}]}$](/math_tex/bd063ba8bc12d419cbf623c598a3d56682.gif) 2.4 2.4
![$(ACP_{n})_{[B_{n-1}, \ldots, B_{0}]}$](/math_tex/bd063ba8bc12d419cbf623c598a3d56682.gif) , analytically solvable 4.2 , analytically solvable 4.2
![$(ACP_{n})_{[B_{n-1}, \ldots, B_{0}]}$](/math_tex/bd063ba8bc12d419cbf623c598a3d56682.gif) , analytically wellposed 4.1 , analytically wellposed 4.1
![$(ACP_{n})_{[B_{n-1}, \ldots, B_{0}]}$](/math_tex/bd063ba8bc12d419cbf623c598a3d56682.gif) , propagator 2.4 , propagator 2.4
![$(ACP_{n})_{[B_{n-1}, \ldots, B_{0}]}$](/math_tex/bd063ba8bc12d419cbf623c598a3d56682.gif) , solution 2.4 , solution 2.4
![$(ACP_{n})_{[B_{n-1}, \ldots, B_{0}]}$](/math_tex/bd063ba8bc12d419cbf623c598a3d56682.gif) , strongly wellposed 2.4 , strongly wellposed 2.4
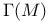 -equicontinuous 1.1 -equicontinuous 1.1
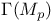 -equicontinuous 1.1 -equicontinuous 1.1
Almost periodic (a.p.) 7.1 7.2
Almost periodic (a.p.), weakly almost periodic (w.a.p.) 7.1
Analytic semigroup of angle  A2 A2
Analytically wellposed in 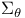 4.1 4.1
Bernstein's theorem 1.5
C-regularized cosine function 1.4
C-regularized semigroup 1.3
Complete 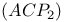 Summary in Chapt. 2 Summary in Chapt. 2
Differentiable semigroup A2
Dissipative operator A2
Elliptic 1.5
Elliptic, strongly elliptic 3.5
Equicontinuous 1.1
Exponential growth bound 5.1
| Exponential growth bound, type 5.3
Exponentially stable 5.1
Fourier multiplier 1.5
Fourier transform 1.5
Hille — Yosidar — Feller — Miyadera — Phillips type theorem 2.2
Incomplete 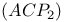 Summary in Chapt. 2 Summary in Chapt. 2
Laplace transform 1.1
Laplace transform, determining function 1.1
Laplace transform, uniqueness theorem 1.1
Lumer — Phillips theorem A2
Moment inequality 4.1
Nonnegative operator 3.6
Nonnegative operator, fractional power A1
Norm continuous 6.2
Parabolic 4.2
Phillips perturbation theorem A2
r-times integrated cosine function 1.4
r-times integrated semigroup 1.4
r-times integrated, C-regularized cosine function 1.4
r-times integrated, C-regularized cosine function, generator 1.4
r-times integrated, C-regularized cosine function, subgenerator 1.4
r-times integrated, C-regularized semigroup 1.3
r-times integrated, C-regularized semigroup, generator 1.3
r-times integrated, C-regularized semigroup, subgenerator 1.3
Strongly continuous 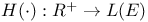 1.1 1.1
Strongly continuous cosine function A2
Strongly continuous cosine function, generator A2
Strongly continuous group A2
Strongly continuous group, generator A2
Strongly continuous semigroup A2
Strongly continuous semigroup, generator A2
Strongly continuous semigroup, strongly continuous semigroups of contractions A2
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



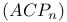
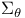
![$(ACP_{n})_{[B_{n-1}, \ldots, B_{0}]}$](/math_tex/bd063ba8bc12d419cbf623c598a3d56682.gif)
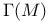 -equicontinuous
-equicontinuous 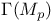 -equicontinuous
-equicontinuous