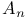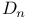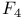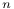|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Tits J. — Buildings of Spherical Type and Finite BN-Pairs |
|
|
 |
| Предметный указатель |
 - morphism of projective spaces over - morphism of projective spaces over  8.4.5 8.4.5
 - projective line 8.12.1 - projective line 8.12.1
 - isomorphism of projective lines 8.12.1 - isomorphism of projective lines 8.12.1
 - quadratic form 8.2.1 - quadratic form 8.2.1
 antiautomorphism of a division ring, antihermitian form 8.1.2 antiautomorphism of a division ring, antihermitian form 8.1.2
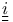 - reduced subset of the index set, for a Coxeter matrix 12.1 - reduced subset of the index set, for a Coxeter matrix 12.1
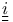 - reduction of a subset of the index set, for a Coxeter matrix 12.1 - reduction of a subset of the index set, for a Coxeter matrix 12.1
 - mapping 6.11 - mapping 6.11
 admissible map, admissible pair 4.10 admissible map, admissible pair 4.10
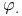 admissible map, admissible mapping 6.11 admissible map, admissible mapping 6.11
( , ,  ) - quadratic form 8.2.1 ) - quadratic form 8.2.1
Absolutely almost simple algebraic group 5.7.3
Adjacence-preserving mapping 3.21
Adjacent chambers 1.3
Adjacent chambers, subspaces of a polar space 8.9.2
Adjoint group 5.7.3
Admissible map (in the definition of projective lines) 8.12.1
Alternating form 8.1.2
Antiautomorphism of a division ring 8.1.1
Antisymmetric form 8.1.2
Apartment 3.1
ASSOCIATED see Polar space
Associated, (polarity - to a projective pseudo-quadratic form) 8.4.1
Associated, (reflection - with a folding) 1.12
Associated, (root - with a folding) 1.12
Associated, (sesquilinear form - to a pseudo-quadratic form) 8.2.3
Automorphism of a projective space 6.2
Bilinear form 8.1.1
BN-pair 3.2.1
BN-pair, (saturated - ) 3.2.5
Bruhat decomposition 3.2.4
Building 3.1 3.26
Building, of a reductive group over a field 5.3
Bushel of circles in a conformal space 9.4.3
Cayley plane ( = octonion projective plane) 5.12
Center of a bushel 9.4.3
Center of a bushel, of a retraction 3.3
Center of a bushel, of a translation of a projective line 8.12.1
Chain of elements in a complex 1.1
Chamber 1.3
Chamber, complex 1.3
Chamber, subcomplex 1.5
Circle of a conformal space 9.4.1
Codimension of an element of a chamber complex 1.3
Codimension of an element of a chamber complex, of an element of a complex in an other 1.1
Coherent mappings 4.13
Collinear points in a polar space 7.1
Collineation of a projective space 6.2
COMPLEX 1.1
Cone of a polar space 7.2.6
Conformal space 9.4.1
Conformal space, structure 9.4.1
Congruent pairs of elements of a building 12.6
Connected component of a subset of the index set, for a Coxeter matrix 12.11
Connected subset of the index set, for a Coxeter matrix 12.11
Connectedness (property of chamber complexes) 1.3
Contained (element of a complex - in another) 1.1
Convex hull of a subset of a chamber complex 1.5
Convex hull of a subset of a chamber complex, hull of a set of roots 13.22
Convex hull of a subset of a chamber complex, set of chambers 1.5
Convex hull of a subset of a chamber complex, set of roots 13.22
Convex hull of a subset of a chamber complex, subcomplex 1.5
Coordinate system in a Moufang projective plane 9.11.2
Corank of a pseudo-quadratic form 8.2.3
Corank of a pseudo-quadratic form, of a reflexive sesquilinear form 8.1.2
Coxeter complex 2.1
Coxeter diagram 2.11
Coxeter diagram, group 2.11
Coxeter diagram, matrix 2.11
Coxeter diagram, system 2.11
Defect of a projective pseudo-quadratic form 8.4.1
Defect of a projective pseudo-quadratic form, of a pseudo-quadratic form 8.2.3
Desarguesian building of type A 6.5
Desarguesian building of type A, pair of vertices in the diagram of a building 6.5
Desarguesian building of type A, projective space 8.3.1
Diagram over a set or a simplex 2.11
Diagram over a set or a simplex, of a building 3.8
Diagram over a set or a simplex, of a Coxeter complex 2.11
Diagram over a set or a simplex, underlying a Dynkin diagram 5.11
Diameter of a chamber complex 1.3
Dimension of a conformal space 9.4.2
Dimension of a conformal space, of a projective space 6.2
Dimension of a conformal space, of a subspace of a polar space 7.1
Dimension of a conformal space, of a subspace of a projective space 8.3.1
Direct sum of two diagrams 2.11
Distance of two elements of a chamber complex 1.3
Distinguished generating set of the Weyl group of a BN-pair 3.2
Dominant embedding of a polar space 8.5.2
Dominated (a subspace - by another) 12. l8
Dual of a generalized 4 - gon 7.2.8
Dual of a generalized 4 - gon of a metasymplectic space 10.13
Dual of a generalized 4 - gon of a polar space of rank 2 7.2.8
Dynkin diagram of a reductive group 5.1
Effective BN-pair 11.14
Embeddable polar space 8.5.2
Embedding (projective - of a polar space ) 8.5.2
Extension of a group by an other 5.9
Extremal element of a strictly convex set of roots 13.25
Extremities of a gallery 1.3
Face of an element of a complex 1.1
Finite type (Coxeter diagram of - - ) 2.17
Flag complex 1.2
Flag complex, complex of a metasymplectic space 10.13
Flag complex, complex of a polar space 7.3
Flag complex, complex of a projective space 6.2
Folding of a chamber complex 1.8
Frame in a projective space 6.2
Frame in a projective space, in a polar space ( = polar frame) 7.3
Full convex hull of a subset of a chamber complex 1.5
Fundamental simplex of a building 3.8
Fundamental simplex of a building, simplex of a Coxeter complex 2.5
gallery 1.3
Generalized m - gons 3.34
Grassmannian of a space 12.1
Grassmannian of a space of a subspace of a space 12.21
Ground field of a building of type A , D or E 6.13
Ground field of a building of type A , D or E, field of a conformal space 9.4.2
Ground field of a building of type A , D or E, ring of a projective line 8.12.1
Half-apartment 3.20
Hermitian form ( - hermitian form, ( - hermitian form, (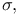 \varepsilon$) - hermitian form) 8.1.2 \varepsilon$) - hermitian form) 8.1.2
Homothetic transformation of a conformal space 9.4.9
Hull (convex - , full convex - ) 1.5
Hypersphere of a conformal space 9.4.1
Image of a polarity in a quotient space of a projective space 8.3.2
incidence 1.2 3.34
Incident elements of a complex 1.1
Incident elements of a complex, point and line 3.34
Incident elements of a complex, subspaces of a polar space 7.3
Incident elements of a complex, subspaces of a projective space 6.2
Induced projective embedding of a cone 8.5.3
Initial embedding of a polar space 8.5.2
Inversion of a conformal space with respect to a hypersphere 9.4.4
Involution of a division ring 8.1.2
Involution of a division ring, (opposition - ) 2.39 . 3.22
Irreducible Coxeter complex 2.11
Irreducible Coxeter complex, diagram 2.11
Irreducible Coxeter complex, type (building or BN pair of - ) 11.1
Isomorphic polarities 8.3.2
Isomorphic polarities, projective pseudo-quadratic forms 8.4.1
Isomorphism of projective lines 8.12.1
Isotropic see Totally
J - reduced element of a building 12.14
J - reduction of an element of a building 12.14
Join of two complexes 1.1
Kernel of a morphism of projective spaces 8.3.1
Length of a gallery 1.3
Line of a generalized m - gon 3.34
Line of a generalized m - gon, of a metasymplectic space 10.13
Line of a generalized m - gon, of a polar space 7.1
Linear subspace of a polar space 7.1
| Linear subspace of a projective space 6.2
Metasymplectic space 10.13
Minimal gallery 1.3
Morphism of chamber complexes 1.3
Morphism of chamber complexesof complexes 1.1 1.3
Morphism of chamber complexesof projective embeddings of polar spaces 8.5.2
Morphism of chamber complexesof projective spaces 8.3.1
Moufang building of spherical type Addenda p.
Moufang building of spherical type, generalized polygon Addenda p.
Moufang building of spherical type, projective plane ( = Cayley plane) 5.12
n - dimensional projective space 6.2
Natural numbering or ordering of the vertices of the diagram 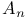 6. 1 6. 1
Natural numbering or ordering of the vertices of the diagram 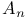 , numbering or ordering of the vertices of the diagram , numbering or ordering of the vertices of the diagram 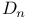 7.12 7.12
Natural numbering or ordering of the vertices of the diagram 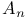 , numbering or ordering of the vertices of the diagram , numbering or ordering of the vertices of the diagram 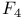 10.1 10.1
Natural numbering or ordering of the vertices of the diagram 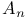 , numbering or ordering of the vertices of the diagram , numbering or ordering of the vertices of the diagram 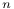 7.4 7.4
Nibbling sequence of roots 13.25
Non-degenerate polarity 8.3.2
Non-degenerate polarity, projective pseudo-quadratic form 8.4.1
Non-degenerate polarity, pseudo-quadratic form 8.2.3
Non-degenerate polarity, reflexive sesquilinear form 8.1.2
Norm form of a conformal space 9.4.2
Octonion projective plane ( = Cayley plane) 5.12
Opposite chambers of a Coxeter complex 2.36
Opposite chambers of a Coxeter complex, elements of a building 3.22
Opposite chambers of a Coxeter complex, elements of a Coxeter complex 2.39
Opposite chambers of a Coxeter complex, foldings 1.12
Opposite chambers of a Coxeter complex, roots 1.12
Opposite structures of projective lines 8.12.1
Opposite structures of projective lines, types of elements of a building 3.22
Opposition involution of a Coxeter complex or of its typical simplex 2.39
Opposition involution of a Coxeter complex or of its typical simplex, involution of the typical simplex of a building 3.22
Orientation of an even dimensional conformal space 9.4.11
Oriflamme complex 7.12
Orthogonal indices, for a Coxeter Matrix 12.11
Orthogonal indices, for a Coxeter Matrix, subsets of the index set, for a Coxeter matrix 12.11
Orthogonality with respect to a pseudo-quadratic form 8.2.3
Orthogonality with respect to a pseudo-quadratic form, with respect to a reflexive sesquilinear form 8.1.2
Parabolic subgroup relative to a BN-pair 3.2.2
Pencil of lines in a Moufang projective plane 9.4.1
Perpendicular hypersphere and circle in a conformal space 9.4.3
Plane of a metasymplectic space 10.13
Plane of a metasymplectic space, of a polar space 7.1
Point of a generalized m - gon 3.34
Point of a generalized m - gon, of a polar space 7.1
Polar frame 7.3
Polar space 7.1
Polar space, space associated to a non-degenerate polarity or to a reflexive sesquilinear form 8.3.4
Polar space, space associated to a projective pseudo-quadratic form or to a pseudo-quadratic form 8.4.2
Polarity 8.3.2
Prelinear set in a polar space 7.2
Projection of an element of a building onto another 3.19
Projection of an element of a building onto another, of an element of a Coxeter complex onto another 2.30
Projective embedding of a polar space 8.5.2
Projective line over a division ring 8.12.1
Projective pseudo-quadratic form 8.4.1
Projective quadratic form 8.4.1
Projective space 6.2 8.3.1
Projective space, space of a vector space 8.3.1
Projective space, space over a division ring 8.4.5
Proportional pseudo-quadratic forms 8.2.2
Proportional pseudo-quadratic forms, sesquilinear forms 8.1.1
Pseudo-quadratic form relative to 0' and e 8.2.1
Quadratic form 8.2.1
Quotient of an embedding of a polar space 8.5.2
Quotient of an embedding of a polar space, of a projective space by a subspace 8.3.1
Rank of a complex 1.1
Rank of a diagram 2.11
Rank of a polar space 7.1
Rank of a polarity 8.3.2
Rank of a projective pseudo-quadratic form 8.4.1
Rank of a pseudo-quadratic form 8.2.3
Rank of a reflexive sesquilinear form 8.1.2
Rank of a subspace of a projective space 6.3 8.3.1
Rank of an element of a complex 1.1
Ratio of a similitude 9.4.7
Ray of a vector space 8.3.1
Reductive group 5.1
Reflection associated with a folding 1.12 12.1
Reflection with respect to an element of codimension one 1.12
Reflexive sesquilinear form 8.1.2
Relative convex hull 4.4
Relatively convex set of chambers 4.4
Relatively convex set of chambers, simple subspace of a subspace 12. 21
Represented (polarity - by a sesquilinear form) 8.3.2
Represented (polarity - by a sesquilinear form), (projective pseudo-quadratic form - by a pseudo-quadratic form) 8.4.1
Retraction of a building onto an apartment 3.3
Root associated with a folding 1.12
Same type (elements of the - - in a building) 3.8
Same type (elements of the - - in a building), type (elements of the - - in a Coxeter complex) 2.5
Saturated BN-pair 3.2.5
Semi-similitude relative to a pseudo-quadratic form 8.2.8
Semi-similitude relative to a pseudo-quadratic form, relative to a reflexive sesquilinear form 8.1.7
Semi-simple group 5.1
Separate (property of three subsets of the index set, for a Coxeter matrix) 12.11
Sesquilinear form relative to  ( = ( =  - sesquilinear form) 8.1.1 - sesquilinear form) 8.1.1
Sesquilinearized of a pseudo-quadratic form 8.2.3
Shadow of an element of a complex on a subset 12.1
Similitude relative to a pseudo-quadratic form 8.2.2 9.4.7
Similitude relative to a pseudo-quadratic form, relative to a reflexive sesquilinear form 8.1.7
Simple subspace of a space 12. l8
simplex 1.1
Simplex, (typical or fundamental - of a building) 3.8
Simplex, (typical or fundamental - of a Coxeter complex) 2.5
singular see Totally
Space 12.1
Space of type (M , J) 12.1
Spanned (subspace of a projective space - by a subset) 8.3.1
Special endomorphism of a building 3.8
Special endomorphism of a Coxeter complex 2.5
Special endomorphism of a Coxeter complex, isogeny 5.7.3
Spherical type (Coxeter complex of - - ) 2.17
Stammer (for a gallery) 1.3
Star of an element of a complex 1.1
Stretched (gallery - between two elements of a chamber complex) 1.3
Strictly convex set of roots 13.22
Strictly convex set of roots, special isogeny 5.7.3
Subcomplex 1.1 1.5
Subspace of a conformal space 9.4.1
Subspace of a conformal space, of 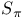 8.4.4 8.4.4
Subspace of a conformal space, of a polar space 7.1
Subspace of a conformal space, of a projective space 8.3.1
Subspace of a conformal space, of a space 12.1
Subspace of a conformal space, of a subspace 12.21
Symmetric form 8.1.2
Symplecton 10.13
Tangent subspaces of a conformal space 9.4.3
Thick chamber complex 1.3
Thick chamber complex, generalized m - gon 3.34
Thick chamber complex, metasymplectic space 10.13
Thick chamber complex, polar space 7.3
Thick chamber complex, projective space 6.2
Thick chamber complex, space 12.1
Thin chamber complex 1.3
Thin chamber complex, metasymplectic space 10.13
Thin chamber complex, polar space 7.3
Thin chamber complex, projective space 6.2
Totally isotropic subspace, for a polarity 8.3.2
Totally isotropic subspace, for a polarity, isotropic subspace, for a reflexive sesquilinear form 8.1.3
Totally singular subspace, for a projective pseudo-quadratic form 8.4.1
Totally singular subspace, for a projective pseudo-quadratic form, singular subspace, for a pseudo-quadratic form 8.2.6
Trace type (polarity of - ) 8.3.2
Trace-valued reflexive sesquilinear form 8.1.4
Translation of a conformal space 9.4.9
Translation of a conformal space of a projective line 8.12.1
Type of a chain of elements of a building 3.9
Type of a chain of elements of a building (M , J) (space of - ) 12.1
Type of a chain of elements of a building of a Coxeter system 2.11
Type of a chain of elements of a building of a subspace of a space 12.18
Type of a chain of elements of a building of a weak building 6.1
Type of a chain of elements of a building of an element of a building 3.8
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 - morphism of projective spaces over
- morphism of projective spaces over  - isomorphism of projective lines
- isomorphism of projective lines  - quadratic form
- quadratic form 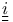 - reduced subset of the index set, for a Coxeter matrix
- reduced subset of the index set, for a Coxeter matrix  - mapping
- mapping 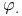 admissible map, admissible mapping
admissible map, admissible mapping  ) - quadratic form
) - quadratic form 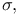 \varepsilon$) - hermitian form)
\varepsilon$) - hermitian form)