|
Электронная библиотека Попечительского совета механико-математического факультета Московского государственного университета |
| Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск |
© Электронная библиотека попечительского совета мехмата МГУ, 2004-2026 |
|
О проекте |
|
О проекте
|



 (derivate)
(derivate)  (cluster set)
(cluster set) 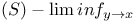
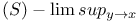
 (interval function limit)
(interval function limit) 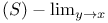 (point function limit)
(point function limit) 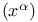 -porosity
-porosity 

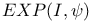
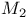 -property
-property 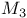 -property
-property 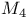 -property
-property 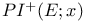 ,
, 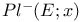

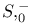

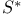 (dual system)
(dual system) 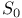

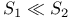

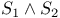
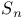
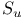
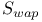
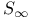
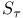




![$[J_1]$](/math_tex/7213892f301cac3c3d44af77a8f7c41282.gif)
![$[J_2]$](/math_tex/2c627661068fa653811187d315e1fe8d82.gif)
![$[J_3]$](/math_tex/61846b3ad86ba38b5d7769fce2c1415582.gif)
![$[J_4]$](/math_tex/17b010bec482ff42218c78b12187d1f582.gif)
![$[Z_{\lambda}]$](/math_tex/09322b0fd62506ddac73f8b7fe94ed9082.gif)
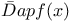 ,
,  (approximate derivates)
(approximate derivates) 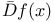 ,
, 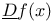 (bilateral derivates)
(bilateral derivates)  ,
, 
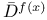 ,
,  (sharp derivates)
(sharp derivates) 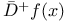 ,
, 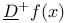 (Dini derivatives)
(Dini derivatives) 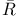
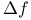
 (Lebesgue — Stieltjes measure)
(Lebesgue — Stieltjes measure) 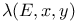

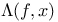
 ,
, 

 -porosity
-porosity  -porous
-porous 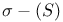 -negligible
-negligible  -porosity
-porosity