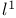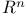|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Taylor R.L. — Stochastic Convergence of Weighted Sums of Random Elements in Linear Spaces |
|
|
 |
| Предметный указатель |
Banach space condition 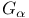 97 97
Banach space convex of type (B) 86
Banach space, definition 9
Banach space, the space 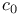 10 10
Banach space, the space 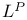 11 11
Banach space, the space 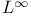 11 11
Banach space, the space c 10
Banach space, the space C[0,1] 10
Banach space, type p 102
Beck and Giesy's Strong Law of Large Numbers 82—83
Beck's Strong Law of Large Numbers for B-convex spaces 86—96
Bochner integral 39
Borel function 12
Borel subsets 12
Borel subsets in D[0,1] 161
Completeness 7
Consistent decision procedure 191
Consistent decision procedure consistent with convergence in probability 191
Convergence comparisons 29
Convergence complete 67
Convergence in D[0,1] 154—165
Convergence in mean 28
Convergence in probability 28
Convergence of series 105
Convergence of series of random elements in 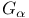 spaces 99—100 spaces 99—100
Convergence of stochastic process 186—190
Convergence of weighted sums of random elements 108—145
Convergence of weighted sums of random variables 63—70
Convergence with probability one 28
Convergence, almost surely 28
Convergence, rates of 105
Convexity also see Geometric Conditions
Convexity and tightness in D[0,1] 166 179—184
Convexity, convex of type (B) 86
Convexity, discussion of 86—875
Convexity, lack of convexity in D[0,1] 158
Convexity, uniformly convex 86
Determining class 31 see
Dual space in characterizing identical distributions and independence 32—33
Dual space in the convergence of weighted sums 110—111
Dual space in the laws of large numbers 75—80
Dual space of a linear topological space 8
D[0,1], basic properties 154—159
D[0,1], characterization of compactness 158
D[0,1], Daffer and Taylor’s SLLN’s 175—179
D[0,1], expected values 159
D[0,1], general introduction 4
D[0,1], Ranga Rao’s SLLN 172—174
D[0,1], topology of the Skorohod metric 154—155
D[0,1], uniform topology 154—155
Family of unicity, definition 31
Family of unicity, examples 31—32
Frechet space, convergence of weighted sums 136
Frechet space, definition 9
Frechet space, laws of large numbers 104—106
Frechet space, the space ![$C[0,\infty]$](/math_tex/d77f73f2c26363b291728c0c8a67a3bc82.gif) 11 11
Frechet space, the space F 11
Frechet space, the space s 9
Generalized Gaussian random variables 66
Geometric conditions convergence of weighted sums 137—145
Geometric conditions convex of type (B) 86
Geometric conditions, 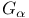 condition 97 condition 97
Geometric conditions, the strong law of large numbers 96—104
Geometric conditions, type p 102—103
Hahn — Banach theorem 13
Hahn — Banach Theorem, use of 27 94
Hilbert space coordinate uncorrelation 61
Hilbert space laws of large numbers 49—54
Hilbert space, definition 9
Hilbert space, the space  11 11
Hoffmann — Jorgensen and Pisier’s Strong Law of Large Numbers 102—103
Identical Distributions and transformations 30—31
Identical Distributions characterized by finite—dimensional distributions 34
Identical Distributions characterized by the dual space 32
Identical Distributions, definition 30
Independence characterized by finite-dimensional distributions 36
Independence characterized by the dual space 32—33
Independence moment conditions in 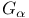 spaces 97—98 spaces 97—98
Independence, definition 30
Inner product in defining uncorrelation 50
Inner product, definition 9
Isometry and Isometric 13
Isomorphism and Isomorphic 13
Ito and Nisio’s convergence of series 105
Kronecker’s lemma 101
Laws of Large Numbers and Geometric conditions 96—104
Laws of Large Numbers in a separable Hilbert space 51—54
Laws of Large Numbers in decision theory applications 190—193
Laws of Large Numbers in Frechet spaces 104—106
Laws of Large Numbers in separable normed linear spaces 71—104
Laws of Large Numbers in type p spaces 102—103
Laws of Large Numbers, Beck and Giesy’s SLLNs 82—83
Laws of Large Numbers, Beck and Warren’s SLLN 80
Laws of Large Numbers, Beck’s SLLN and convexity 86—96
Laws of Large Numbers, convergence of weighted sums 3
Laws of Large Numbers, counterexample in 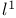 80—81 80—81
Laws of Large Numbers, counterexample in  95 95
Laws of Large Numbers, estimation applications 197—201
Laws of Large Numbers, general discussion 3
Laws of Large Numbers, Hoffman — Jorgensen and Pisier’s SLLN 102—103
| Laws of Large Numbers, Monte Carlo methods 196—197
Laws of Large Numbers, Mourier’s SLLN 72—74
Laws of Large Numbers, SLLN for tight random elements 133
Laws of Large Numbers, SLLNs in D[0,1] 172—179
Laws of Large Numbers, strong laws for random variables 46—48
Laws of Large Numbers, weak law for random variables 43
Laws of Large Numbers, WLLN for tight random elements 129
Laws of Large Numbers, WLLNs in D[0,1] 166—170
Linear Space, definition 6
Linear Space, the linear space D[0,1] 157
Linear topological space 8
Markov’s inequality 29
Measurability Borel 12
Measurability problem 1
Measurability strongly 23
Metric space D[0,1] 157
Metric space, definition 7
Metric space, linear 8
Mourier’s Strong Law of Large Numbers 72—74
Norm definition 8
Norm, normed linear space 8
Norm, of a continuous linear functional 13
Norm, uniform norm for D[0,1] 15
Orthogonal, definition 18
Orthogonal, orthonormal 18
Orthogonal, weakly orthogonal 80
Pettis integral as an expected value 38
Pettis integral, existence of 40—41
Pettis integral, properties of 38—39
Random element(s) in 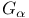 spaces 97—104 spaces 97—104
Random element(s) in 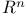 21 21
Random element(s) in a separable Hilbert space 4
Random element(s) in a separable semimetric space 25—26
Random element(s) in D[0,1] 159—165
Random element(s) in R 21
Random element(s), addition of 28
Random element(s), characterized by a Schauder basis 24
Random element(s), characterized by the dual space 27—28
Random element(s), convergence of weighted sums 108—152
Random element(s), countably-valued 22—23
Random element(s), definition 21
Random element(s), expected value of 38 see
Random element(s), identically distributed 30
Random element(s), independent 30
Random element(s), laws of large numbers for 51—54 71—104
Random element(s), limits of 22—23
Random element(s), probabilistic convergence 26
Random element(s), product with a random variable 24
Random element(s), strongly-measurable 23
Random element(s), transformations of 22
Random element(s), type (A) 88
Random element(s), uncorrelated 50
Random element(s), variance of 3 8
Schauder basis characterizing compactness 19
Schauder basis characterizing random elements 24
Schauder basis characterizing the expected value 42
Schauder basis characterizing weakly uncorrelated 56
Schauder basis coordinate functionals 14
Schauder basis coordinate uncorrelation 55
Schauder basis in convergence of weighted sums 112—127
Schauder basis in obtaining laws of large numbers 72—75
Schauder basis partial sum operators 15
Schauder basis, definition 14
Schauder basis, examples 15—18
Schauder basis, monotone 14
Semimetric space 7
Seminorm 8
Separability and random elements 23
Separability stochastic processes 2
Separability, definition 9
Skorohod metric 154
Stochastic Processes and random elements 1
Stochastic Processes stationary increments and identically distributed random elements 35
Stochastic Processes, Brownian motion processes 36
Stochastic Processes, laws of large numbers for 84 186—190
Stochastic Processes, Poisson processes 36
Taylor and Padgett’s Strong Law of Large Numbers 83—84
Taylor’s Weak Laws of Large Numbers 75—79 85
Tightness centering random elements 121
Tightness convergence of weighted sums of random elements 124—134
Tightness for Brownian motion processes 187
Tightness, convex tightness in D[0,1] 166
Tightness, definition 120
Toeplitz sequence 63 109
Uncorrelation and independence 52
Uncorrelation comparisons 55—63
Uncorrelation in a separable Hilbert space 5
Uncorrelation pointwise in D[0,1] 169
Uncorrelation random variables 45
Uncorrelation, coordinate uncorrelated 55
Uncorrelation, weakly uncorrelated 55
Weighted Sums, applications in quality control 195—196
Weighted Sums, convergence and tightness 120—136
Weighted Sums, convergence for random elements 108—152
Weighted Sums, convergence for random variables 63—73
Weighted Sums, convergence of randomly weighted sums 146—151
Weighted Sums, general appearance 2
Weighted Sums, geometric conditions and convergence 137—145
Weighted Sums, random weighting 4
Woycznski’s Strong Law of Large Numbers 101—102
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



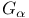
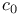
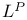
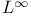
![$C[0,\infty]$](/math_tex/d77f73f2c26363b291728c0c8a67a3bc82.gif)