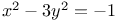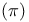|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Olds C.D. — Continued Fractions |
|
|
 |
| Предметный указатель |
Absolute value 72
Acyclic 95
Approximation theorems 70ff
Archimedes 58
Archimedes, “cattle problem” of 90 113
Aryabhata 29
Associate 103
Babylonians 58
Beckenbach, E. 9
Bellman, R. 9
Bombelli, Rafael 29 134
Brouncker, Lord 30 89 135
Cataldi, Pietro Antonio 29 134
Coconuts and monkeys 48ff
conjugate 99
Continued fraction 7
Continued fraction for  112ff 112ff
Continued fraction, finite simple 7
Continued fraction, geometrical interpretation of 77
Continued fraction, infinite simple 53-54 66
Continued fraction, interpretation of 77
Continued fraction, periodic 88ff
Continued fraction, periodic part of 56
Continued fraction, purely periodic 90ff
Continued fraction, simple 7
Continued fraction, symmetrical periodic part of 113
Continued fraction, terminating 7
Continued fraction, uniqueness 11
Convergents 6 19
Convergents, differences of 27 58 61
Coxeter, H.S.M. 61
de Gelder, Jakob 60
Dickson 89-90
Diophantine equations 31ff
Diophantine equations, general 37
Diophantine equations, minimal solution of 118
Diophantine equations, particular solution of 37
Diophantine equations, solutions of 89
Discriminant 98
Divina Proportione 82
e 52 74-75 135-136
Equivalence classes 127
Equivalent 127ff
Eratosthenes 90
Euclid’s algorithm 16
Euclid’s Elements 17
Euler 30 32 35 132 135
Farey sequences 126
Fermat 89 132
Fibonacci numbers 60 81-82 84 137 147
Galois 95
Gardner, Martin 50
Gauss 132 138
Geometric constructions 59
Golden section (mean) 61 82-83
Greatest common divisor 17
Hardy 123 130
Heath 90
Hildebrand, F.B. 30
Hurwitz’s theorem 124ff 128
Huygens, Christiaan 30
Indeterminate equations,  36 36
Indeterminate equations,  46 46
Indeterminate equations, ax + by = c 31
Indeterminate equations, ax + by = c, (a,b) = 1 44
| Indeterminate equations, ax - by = c, (a,b) = 1 42
Indeterminate equations, Diophantine 31ff 89
Indeterminate equations, having no integral solutions 131ff
Indeterminate equations, Pell’s equation,  89 113ff 118ff 123 89 113ff 118ff 123
Indeterminate equations, quadratic equation 121
Integral part of x, [x] 108
Irrational numbers 51ff
Irrational numbers, approximation of 123ff
Irrational numbers, expansion of 51ff
Klein, F. 77
Lagrange 30 56 89 95 139
Lagrange’s Theorem 1 lOff
Lambert 30 136 138
Laplace 139
Lattice points 77
Le Veque 126
legendre 132 136
LIMIT 44 63
Logarithms, common 74
Logarithms, method for calculating 84ff
Logarithms, natural 74
Minkowski 130
Newman, James R. 90
Niven, Ivan 52 123 126 129
Number, algebraic 52
Number, irrational 51ff
Number, prime 19
Number, transcendental 52
Ore, O. 32
Pacioli, Luca 82
Partial quotients 8 19
Partial sums 64-65
Pell, John 89
Pell’s equation,  89 113ff 118ff 123 89 113ff 118ff 123
Pell’s equation,  , insoluble, , insoluble, 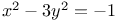 131ff 131ff
Pell’s equation,  , minimal solution of 118 , minimal solution of 118
Perron 129
Phyllotaxis 61
Pi 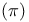 52 58 60 76 136-137 52 58 60 76 136-137
Prime number 19
Pythagorean equation 121
Quadratic irrational 51
Quadratic irrational, reduced 89 96-98 lOOff
Quadratic surd 51 88
Quadratic surd, reduced 96-98 lOOff
Rational fractions, expansion of 5 8 13
Reflexive 127
Rhind papyrus 58
Robinson, R.M. 129
Schwenter, Daniel 29
Segre, B. 129
Serret 132
Shanks, Daniel 84
Smith, D.E. 134
Square root of 2  52 52
Stern 137
Stieltjes 130
symmetric 127
Transitive 127
Uniqueness 16
wall 130
Wallis, John 30 135
Wright 123 130
Wythoff, W.A. 61
Wythoff, W.A., game 61
Zippin, L. 66
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте