|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Adams J.F. Ч Infinite Loop Spaces - Hermann Weyl Lectures the Institute for Advanced Study, Vol. 90 |
|
|
 |
| ѕредметный указатель |
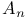 -spaces 33Ч36 -spaces 33Ч36
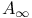 spaces 30Ч35 spaces 30Ч35
 , ,  28 144 28 144
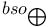 , , 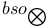 , ,  , ,  28 145Ч146 28 145Ч146
 , ,  28 146 28 146
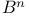 , , 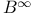 45 47 50 45 47 50
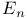 space 44 48 space 44 48
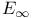 ring space 72 ring space 72
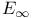 ring spectrum 73 ring spectrum 73
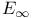 space 46 69 space 46 69
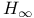 ring spectrum 73 ring spectrum 73
 26 132 134 136Ч137 192 26 132 134 136Ч137 192
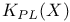 , , 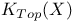 26 132 192 26 132 192
 -topology 186 -topology 186
 57 57
 -space 63 -space 63
 63 63
 -space 64 -space 64
 3 3
 -spectrum 15 -spectrum 15
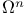 44Ч45 48Ч49 44Ч45 48Ч49
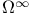 22Ч26 47 49 142Ч43 146Ч147 149Ч155 158 184 186Ч187 22Ч26 47 49 142Ч43 146Ч147 149Ч155 158 184 186Ч187
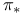 -topology 185Ч186 -topology 185Ч186
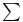 6 6
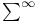 11 15 17 20 22 100Ч101 103Ч107 124Ч127 11 15 17 20 22 100Ч101 103Ч107 124Ч127
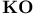 , KO, , KO, 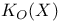 132 134Ч137 145 154 192 132 134Ч137 145 154 192
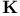 , ,  152 152
 , , 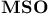 10Ч11 19 10Ч11 19
 71 71
Adams conjecture 132Ч141
Adams conjecture, infinite-loop versions of 195Ч196
Adams, J.F. and Priddy, S.B. (their theorem) 145Ч148
Algebra-functor 53 55Ч56 59
Algebraic K-theory 25 28 70 86Ч87 91 140 196
Approximation theorem 49 56
Araki see УKudoФ
Associativity conditions 30Ч34
Axioms for machines 196
B (classifying space) 34Ч36 50 61 64Ч65 67Ч68
Bar construction 51Ч59
Becker, J.C. and Gottlieb, D.H. (on Adams conjecture) 140Ч141
Becker, J.C. and Gottlieb, D.H. (on transfer) 106Ч108
BF 25Ч26 136 192Ч193 195 see
BO 16 19 28 132 141 192
Boardman, J.M. and Vogt, R.M. 25 37 46 47 50Ч51 60
Boardman, J.M., (his category) 11
Boardman, J.M., (on transfer) 100 see
Bounded below 21
BPL 25Ч26 192
bso 145
bsu, BSU 154
BTop 25Ч26 192
BU 16 19 28
Classifying spaces see entries from УBФ to УBUФ
Coefficient groups 20Ч21
Coefficients in generalized homology theories and spectra 74Ч76 153
Coherence conditions 67
Coker, J. 193
Completion 146 153
Connective 21
Connective tissue 60
Coordinate-free spectra 72Ч73
Cup-products 27Ч28 70Ч71
CW-spectra 11Ч12
Discrete models 143 192
Double coset formulae 128Ч131
Double loop-space 13 36
Dyer, E. and Lashof, R.K. 37
Dyer, E. and Lashof, R.K., their operations 24 36 144Ч145
E-space 46
Eilenberg Ч MacLane spaces 15Ч16
Eilenberg Ч MacLane spectra 19
f 25 see
Filtration topology 183 186
Friedlander, E.M. 195
Generalized cohomology theories 16Ч17 20
Generalized homology theories 20
Geometrical realization 58Ч59 61 68
Gottlieb see УBeckerФ
Group completion theorem 90
Grouplike (H-spaces) 88
H-space 12Ч13
H-space structure 33 see
Higher homotopies 34 36 46 65 72 123
Homotopy groups, (of spaces) 5 7
Homotopy groups, (of spectra) 20Ч21
Homotopy-invariant structures 50Ч51
Im J 193
J-homomorphism 133 137 193
| James, I.M. (his model) 8 49
jokes vii 66 200 204
K-theory 16 19 26 27 28 98Ч99 132Ч137 142Ч191
Kahn, D.S. and Priddy, S.B., (on transfer) 104Ч105 119
Kahn, D.S. and Priddy, S.B., (their theorem) 24 105
Kan, D.M. and Thurston, W.P. 84
Kudo, T. and Araki, S. 24 36 37
Lashof see УDyerФ
Limit topology 184
Little cubes operad 46 119
Little n-cubes operad 42Ч44 119
localization 74Ч82 135Ч136 148 151 153
Loop-spaces 3 12
Machinery 30 36Ч37 196
Madsen, I., Snaith, V.P. and Tornehave, J. 194
Madsen, I., Snaith, V.P. and Tornehave, J., their theorem 148Ч191
Madsen, I., Snaith, V.P. and Tornehave, J., their theorem, global version 149Ч151
Madsen, I., Snaith, V.P. and Tornehave, J., their theorem, local version 153Ч155
May, J.P. 26 37 41 46 50Ч51 56 59 155 194 196
Module-functor 55Ч56 59
Monad 53 56 59
Monoidal category 66 67
Moore, J.C, (his loops) 31
Moore, J.C,(his space) 74Ч75
Morse, M. 3Ч4
Multiplicative structures 27Ч28 70Ч73
Nerve (of a category) 68
Operad 41Ч44 56 59 see УLittle
Orientations 26 194
p-adic topology 184
Parameter spaces 33 37 41 60
Permutative category 67 88 143 196
PL 25Ч26 192
Plus construction 84Ч88 91 105 140
Pontryagin product 13
Pre theorems 45
Pretransfer 119
Priddy, S.B., (his theorem on  ) 83Ч84 see УKahnФ ) 83Ч84 see УKahnФ
Products see УCupЧproductsФ УPontryagin УMultiplicative
PROP 37Ч42 51
Quillen, D.G. 82Ч83 84Ч87 91 138Ч140
Realization see УGeometrical realizationФ
Recognition principle 49
Representing spectrum 17Ч19 21
Ring-object, ring-space, ring-spectrum 71Ч73
Segal, G.B. 27
Segal, G.B. and his machine 59Ч65 196
Series topology 185
Serre, J.-P. 4-5 74
Seymour, R.F. 195
Simplicial sets and spaces 57Ч58
Smash product, (of spaces) 20
Smash product, (of spectra) 71 73 127
Snaith see УMadsenФ
Spanier Ч Whitehead duality 9Ч10
Special  -spaces 63 -spaces 63
Special  -spaces 64 -spaces 64
Spectrum, spectra 11 see УCoordinate-free У УEilenberg У У УRepresenting УRing-spectrumФ УSphere УSuspension УThom
Sphere spectrum 19 28
Spherical fibrations 25 133Ч134 136 195 see
Stable homotopy groups 17
Stable homotopy theory 7Ч12
Stasheff, J.D. 33 35 37 41
Strict (monoidal category) 66 69
Structure maps 31Ч34 37 108Ч123
Sugawara, M. 33 35
Sullivan, D. 74 78 137Ч138 147 194
Suspension 6;
Suspension spectrum 11 see
Suspension-theory 8
Symmetric (monoidal category) 67 see
T-functor 55
T-object 54
Thom complexes 11
Thom spectra 11 19 71
Thurston see УKanФ
Top 25-26 192
Topological category 70
Tornehave see УMadsenФ
TRANSFER 96Ч131 145 172Ч183
Trees 51
Triple 53
Uniqueness of machines 196
Universal coefficient theorem 76 167Ч168
Vogt see УBoardmanФ
Weak equivalence 14
Whitehead, G.W. 19 165
Whitney sum 26
Zabrodsky mixing 79
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



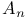 -spaces
-spaces 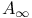 spaces
spaces  ,
, 
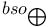 ,
, 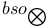 ,
,  ,
, 
 ,
, 
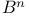 ,
, 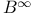
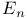 space
space 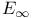 ring space
ring space 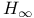 ring spectrum
ring spectrum 
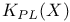 ,
, 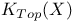
 -topology
-topology 

 -space
-space 
 -spectrum
-spectrum 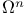
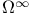
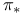 -topology
-topology 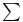
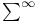
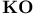 , KO,
, KO, 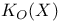
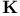 ,
, 
 ,
, 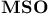

 )
)