Авторизация
Поиск по указателям
Todorchevich S., Farah I. — Some Aplications of the method of forcing
Обсудите книгу на научном форуме Нашли опечатку?
Название: Some Aplications of the method of forcingАвторы: Todorchevich S., Farah I. Аннотация: During the Fall Semester of 1991 Stevo Todorchevich (Todorcevic) gave a course on applications of the method of forcing at the Mathematical Institute in Belgrade. This text contains material presented in the course, as well as some additional closely related results included for completeness. The method of forcing, i.e. the method of adding a generic object to a given structure, is frequently used to get independent results, that is, results showing that certain statements cannot be proved (or disproved) in ZFC or some other similar theory. The main purpose of these notes is to present to a general mathematical audience a number of applications of the method of forcing to other branches of mathematics, such as general topology and measure theory. Most of the presented results do not require any additional axioms of set theory, but use standard set-theoretical and forcing constructions, such as Suslin tree, generic models^ Cohen and random reals, etc. Among topics included are Borel Equivalence Relations, Halpern-Laiichli Theorem, the Open Coloring Axiom and the Proper Forcing Axiom. For more ambitious readers there are a few exercises scattered throughout the text, and a list of yet unsolved problems is included.
Язык: Рубрика: Математика /Серия: Сделано в холле Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1995Количество страниц: 148Добавлена в каталог: 28.10.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
65 5 132 87 32 128 9 68 66 135 66 66 135 Absolute class 125 Algebra of Baire sets 48 Almost disjoint subsets of 73 Antichain (in a poset) 4 Antichain in a tree 17 Arrow-space 93 135 Automatic continuity problem 100 Axiom, Comprehension Scheme 112 Axiom, Extensionality 111 Axiom, forcing axiom 2 Axiom, forcing axioms 63 Axiom, large cardinal axiom 122 Axiom, Martin’s Axiom (MA) 65 Axiom, of choice 114 Axiom, of Foundation 118 Axiom, of infinity 116 Axiom, Open Coloring Axiom (OCA) 79 Axiom, Pairing 111 Axiom, power set 112 Axiom, Proper Forcing Axiom (PFA) 97 Axiom, Replacement Scheme 112 Axiom, union 111 Baire property 128 Baire space 18 Ball of partial functions 87 Base for a class of topological spaces 93 BP Boolean Prime Ideal 41 Branch (of a tree) 17 Caliber (of a topological space) 65 Cantor cube 1 Cardinal 115 Cardinal, limit 116 Cardinal, preserved by 48 Cardinal, regular 118 Cardinal, singular 118 Cardinal, strongly inaccessible 118 Cardinal, successor 116 Cardinal, weakly inaccessible 118 Cardinality 115 Cellularity, of a filter 107 Cellularity, of a topological space 21 Cellularity, of an ideal 103 Centered (family of sets) 65 Closed and unbounded subset of an ordinal 131 Closed subset of an ordinal 131 Code, for a 11 Code, for an open set 11 Codes for Borel sets 130 Codes for Borel sets, 130 Codes for Borel sets, 130 Cofinal 73 Cofinality 118 Cohen real 1 Cohen real, over M 10 Coinitial 73 Comparable 113 Complete accumulation point 137 Composant 107 Continuous family of sets 114 Continuum 66 107 Continuum Hypothesis (or CH) 116 Continuum, decomposable 107 Continuum, linearly ordered 66 Control Measure Problem 110 Correct for some formula 121 Cumulative hierarchy 118 Definition by 114 Dense below p 1 Diadic rationals 133 Diagonalization of the sequence of sets 55 Direct product 112 Discrete subspace 135 Dominating subset of 103 Elementary submodel 124 Equipotent sets 115 Exponential topology 136 Extension of a condition 1 Family of functions, trivial 85 Fills the p re-gap 73 Filter 1 Filter Dichotomy 104 Filter, 1 Filter, Frechet 104 Filter, generic 1 Filter, M-generic 9 Forces 10 Formula, 125 Formula, 126 Formula, absolute 123 Formula, absolute for X 123 Formula, atomic 121 Formula, function-defining 112 Free sequence 136 Free sequence, of regular pairs 67 Function, Baire 48 128 Function, Borel 127 Function, choice 114 Function, order-reversing 33 Function, Skolem 124 Fusion (of the family of sets) 54 Fusion sequence 54 Gap 73 (see also “Pre-gap”) Gap, Borel 86 Gap, Hausdorff 74 Gap, in 73 Gap, in 74 Gap, special 75 Gap, type 73 Generalized Continuum Hypothesis (GCH) 116 Group wise dense subset of 103 Hausdorff metric 137 Height (of a node in a tree) 17 Immediate successor in a tree 41 Incomparable 1 Incompatible 1 Induction (on the ordinals) 114 Inner regularity (of a measure) 69 Interpretation (of a 9 Interval algebra 90 Interval determined by p 1 Invariant subspace problem 110 Isomorphic elements of 50 Isomorphism type of p 50 Large enough part of ZFC 124 Lemma, 5 132 Lemma, Fusion Lemma 54 Lemma, Pressing-Down Lemma 131 Lemma, Truth Lemma of forcing extensions 10 Level (of a tree) 17 lexicographical ordering 3 Lexicographically least infinite branch 33 Measure, 69 Measure, counting 128 Measure, Haar 128 Measure, Lebesgue 128 Measure, product 128 Measure, regular Radon 69 Model 121 Model, generic 9 Model, ground 9 Models (a relation) 121 Mokobodzki ideal 13 NCF (Near Coherence of Filters) 107 Network 93 135 OCA(X) 79 OCA* 80 Operator, compact 107 Order type 42 113 Ordering, linear 113 Ordering, partial 113 Ordering, total 113 Ordinal 113 Ordinal, limit 113 Ordinal, successor 113 Outer regularity (of a measure) 69 P-ideal 85 Partition, open 79 Partition, Sierpiriski’s 44 Partition, Suslin (or ccc) 63 Pattern, of elements of 46 Pattern, of elements of 58 Perfect Set Property.(PSP) 80 Perfect-set Forcing 54 Polish space 127 POSET 1 113 Poset, 99 Poset, 97 Poset, ccc 5 Poset, of partial functions 85 Poset, proper 97 (see also “Baumgartner 1984” “Shelah Pre-gap 73 Pre-gap, cofinal 74 Pre-gap, equivalent 74 Pre-gap, fillable (or split table) 73 Pre-gap, Suslin pre-gap 76 Precaliber (of a topological space) 65 Prenex normal form (PNF) 123 Product of posets 1 Projection of a tree 32 Proof by 114 Proper class 111 Property of Baire 19 Quasi-ordering 42 Random real 2 Random real, over M 12 Rank 119 Reals 127 Recursion (on ordinals etc). 114 Reducible coloring, regular pair 67 Relation, antisymmetric 113 Relation, Borel (analytic, coanalytic, etc). 31 Relation, Borel (analytic, coanalytic, etc)., functional 112 Relation, Borel (analytic, coanalytic, etc)., reflexive 113 Relation, Borel (analytic, coanalytic, etc)., set-like 113 Relation, Borel (analytic, coanalytic, etc)., transitive 113 Relativization (of the formula) 121 Restriction 112 Root (of a 5 RVM 21 Sacks real 54 Separated 135 Separates 98 Set, 127 Set, 99 Set, 69 Set, 130 Set, 0-homogeneous 4 Set, analytic 127 Set, Borel 127 Set, coanalytic 32 127 Set, comeager 13 128 Set, countable 116 Set, dense 1 Set, empty 112 Set, extension al 120 Set, free for F 71 Set, hereditarily countable 121 Set, hereditarily finite 121 Set, homogeneous 42 Set, homogeneous for f 41 Set, infinite 116 Set, meager 2 128 Set, n-dense 49 Set, nowhere dense 128 Set, null 2 Set, of conditions 1 Set, of first category 2 Set, open (in a poset) 9 Set, partially ordered 113 Set, Skolem hull 124 Set, Sorgenfry line 93 135 Set, stationary 131 Set, stationary, transitive 113 Splits the pre-gap 73 Splitting node in a tree 41 Submeasure 110 Submeasure, exhaustive 110 Subtree 41 Subtree, of 32 Support of a Baire set 48 Suslin Hypothesis (SH) 17 Suslin property 5 Terminal node of a tree 33 Theorem, Baire category 128 Theorem, Bernstein — Robinson 110 Theorem, Cantor 115 Theorem, Cantor — Bernstein 115 Theorem, Compactness Theorem of Predicate Calculus 124 Theorem, Dense Set Version of 49 Theorem, Dilworth’s 38 Theorem, Godel’s Incompleteness 121 Theorem, Helly’s 102 Theorem, HL (Halpern — Laiichli) 41 Theorem, HL, finite version 49 Theorem, Maharam’s 25 Theorem, Mostowski’s Collapsing 120 Theorem, Ramsey’s 131 Theorem, Reflection 123 Theorem, Shoenfield’s Absoluteness 35 Theorem, Ulam’s 28 Theorem, Zermelo 115 Tightness 66 136 Topological space, 135 Topological space, 135 Topological space, Baire 128 Topological space, ccc 21 Topological space, cometrizable 94 Topological space, countably compact 136 Topological space, countably tight 66 136 Topological space, exponential 94 Topological space, Hausdorff (or 135 Topological space, regular (or 135 Topological space, second countable 79 Topological space, Suslin 21 Transitive closure 119 TREE 17 Tree representation, of analytic sets 32 Tree representation, of coanalytic sets 32 Tree, 17 Tree, Aronszajn 17 Tree, perfect 41 Tree, Suslin 17 Tree, well-founded 32 Ultrafilter, nonprincipal 52 Ultrafilter, Ramsey 55 Ultrafilter, selective 55 Vertical sections 13 Vietoris topology 136 Weakly separated 94 Weight 135 Well-founded 113
Реклама
 |
|
О проекте
|
|
О проекте



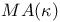
 -system
-system  -ball around h
-ball around h  -operation
-operation  -name
-name 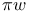 -homogeneous
-homogeneous  -base
-base 
 -set
-set 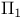
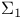
 -recursion
-recursion 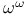
 -generic
-generic 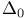
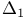
![$[\omega]^{\omega}$](/math_tex/07fea37923158b9194961bd75f36321882.gif)

 -finite
-finite 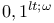

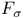 ,
, 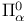 ,
, 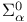
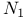 -dense
-dense  -supporting
-supporting 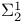

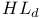
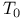
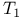
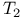 )
) 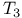 )
) 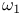 -tree
-tree