|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Lang S. Ч Diophantine Geometry |
|
|
 |
| ѕредметный указатель |
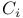 property 245Ч249 property 245Ч249
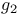 and and 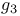 12 126 12 126
 -degree 173 -degree 173
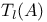 82 94 82 94
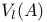 83 83
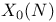 127Ч131 127Ч131
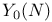 and and 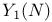 127 127
abc conjecture 29 47 49 65
Abelian logarithm 237
Abelian varieties 16 20 25Ч42 68Ч100 101Ч122 158Ч162 181Ч183 220 221 232 236Ч239
Abelian varieties, equations for 26 77 УBirch УDescentФ УFaltingsФ УFinitenessФ УFunction УGauss УJacobianФ Уl-adic УLang УManinТs УMasser УModuliФ УMordell УNeron УNeron УParshinФ УPolarizationФ УRankФ УRaynaudФ УSemisimplicityФ УSemistableФ УSubvarietiesФ УTate УTheorem УTorsion УTrace
Absolute case 12
Absolute conjecture 67
Absolute norm 55
Absolute value 44
Adams type for e 214
Adeles 93
Adjunction formula 168
Admissible metric 165
Affine bounded 207
Affine coordinate ring 4
Affine coordinate ring, coordinates and integral points 217
Affine variety 2
Ahlfors on Nevanlinna theory 199 203
Ahlfors Ч Schwarz lemma 185
Ahlfors Ч Shimizu height 200
Albanese variety 31 32
Albert Ч Brauer Ч Hasse Ч Noether theorem 252Ч253
Algebraic equivalence 30 33
Algebraic families 12 18 23Ч27 28 62 74Ч82 118Ч121 158Ч162 178 187 189 192 221
Algebraic families of abelian varieties 27 28 74Ч82 118Ч121 158Ч162 189
Algebraic families of heights 76Ч82
Algebraic families of pseudo-canonical varieties 24 25
Algebraic families, split 12 24 25 62 78 79 178 192 УFunction УManin УSilverman
Algebraic integers 54
Algebraic point 3
Algebraic point in VojtaТs conjecture 50 63Ч67 222Ч225
Algebraic special set 16 182
Algebraically hyperbolic 16 17 179
ample 7 11Ч15 20 22 67 181 198
Ample, anti-canonical class 19 20 67
Ample, canonical class 14 15 18 22 198
Ample, cotangent bundle 181
Ample, vector sheaf 20
Analytic torsion 173 175
Anticanonical class 15 19 20 67 169 245 258Ч262
Anticanonical varieties 15 259Ч262
Arakelov, degree 168
Arakelov, height 169
Arakelov, inequality 151
Arakelov, metric 165
Arakelov, Picard group 167
Arakelov, Shafarevich conjecture in function field case 104
Arakelov, theory 71 163Ч171 228 230 231
Arakelov, volume form 166
Arithmetic Chern character 173
Arithmetic Chow group 174
Arithmetic discriminant 64 171
Arithmetic discriminant and VojtaТs inequality 171
Arithmetic Euler characteristic 173
Arithmetic Picard group 167
Arithmetic surface 166
Arithmetic Todd class 173
Arithmetic variety 171
Artin theorem on local specialization 259
Artin Ч Tate 250 253
Artin Ч Winters 150
Artin, conductor 71
Artin, conjectures on 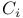 fields 246Ч247 fields 246Ч247
Ax theorems, one-parameter subgroups 182
Ax theorems, quasi-algebraic closure 246
Ax Ч Kochen theorem 247
Baily Ч Borel compactification 118
Baker 235 237 239 240
Baker Ч Feldman inequality 235
Basic Hilbert subset 41
Basic isogeny problem 121
Batyrev 20 262
Batyrev Ч Manin conjectures 260Ч262
Batyrev Ч Manin conjectures, relation with Vojta conjecture 261
Beilenson Bloch conjectures 34
Biduality 33
Birational map 5
Birationally equivalent 5
Birch 148 248
Birch Ч Swinnerton Ч Dyer conjecture 34 91 92 94Ч96 98 136 137 139Ч140
Birch Ч Swinnerton Ч Dyer conjecture, Coates Ч Wiles 136
Birch Ч Swinnerton Ч Dyer conjecture, Gross Ч Zagier 139Ч142
Bismut Ч Vasserot 174 232
Bloch (Andre) conjecture 182
Bloch (Spencer) conjectures 34
Bogomolov 20 151
Bombieri simplification of VojtaТs proof 233
BorelТs theorem 183
Bosch 259
Bounded degree 56 63 64 204 222 223
Bounded degree, denominator 217
Bounded degree, generated group 240Ч243
Bounded degree, height see УHeight upper
Brauer group 250Ч258
Brauer group, birational invariant 252
Brauer group, exact sequence 255
Brauer group, unramified 252
Brauer Ч Grothendieck group 250 252
Brauer Ч Grothendieck group, specialization 252
Breen 80
Brody hyperbolic 178 179 183 184 225 226
Brody Ч Green hypersurface 22 181 186
BrodyТs theorem 179
Brownawell-Masser 66
Brumer Ч McGuinness on average rank 28
Bryuno 214
Canonical bundle 185
Canonical class 11 14 20 21 119 146 151 152 197
Canonical class, in higher dimension 14
Canonical class, inequalities 151 152
Canonical class, on a curve 11
Canonical class, on moduli space 119
Canonical class, on projective space 14 197
Canonical class, relative 146
Canonical class, zero 19Ч21 23
Canonical height 63 64 67 146 169
Canonical height in Nevanlinna theory 202
Canonical metric 165 166
Canonical sheaf 119 145 146 169 170 228 259
Canonical sheaf of an imbedding 145 146 169
Canonical variety 15
Carlsson Ч Griffiths on Nevanlinna theory 201
Cartan Ч Nevanlinna height 194
CartanТs theorem 197Ч198
Cartier divisor 6 14
Cartier divisor, divisor class group 6
Cassel Ч Guy example 254
Cassels Ч Tate pairing 89
CC inequalities 151 152
Chabauty 36 38
Chai on cubical sheaves 80 82
Chai Ч Faltings 118 120 122
ChaiТs theorem of the kernel 158
Characteristic polynomial 85
Chatelet Ч Weil group 87 88
Chatelet, Brauer variety 256
Chatelet, surface 22 256 257
Chern form 184 202
Cherry on Nevanlinna theory 204 223
Chevalley Ч Weil theorem 224
ChevalleyТs theorem on quasi-algebraic closure 246
Chow group 7 33 174
Chow group in higher codimension 34
Chow trace 26 (see also УLang Ч NeronФ УTrace
| Chow Ч Lang 69 103
Circle method 248
Class field theory 105
Clemens curves 21 34
Co Ч Lie determinant 116 118
Coates Ч Wiles theorem 136
Cocycle 153
ColemanТs account of ManinТs method 153Ч161
Colliot Ч Thelene 249Ч258
Colliot Ч Thelene, conjecture 254
Compact case of Vojta conjecture 67
Complete intersection 4
Complex multiplication 29 39 136
Complex torus 125
Complex torus, isomorphism classes 126
Complexity of divisor 203
Conductor 51 71 97Ч99
Conductor of elliptic curve 97Ч99 (see also УModular elliptic curvesФ)
Congruent numbers 135
Connected component 31 33
Connected component, Neron model 70 79Ч81 98
Connection 154
Conormal sheaf 145 169
Constant field 12
Counting function 193 202 211
Counting, algebraic integers 57
Counting, points 58 61 73 260Ч262
Counting, units 57
Coverings, applied to diophantine approximations 219 222
Coverings, descent and heights 37 85 160
Coverings, Nevanlinna theory 204
Coverings, Parshin construction 104Ч106
Coverings, ramified 104Ч105 224 225
Coverings, torsion points 39
Coverings, X_0(N)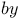 X_1(N)$ 128 X_1(N)$ 128
Cubic forms 22 247 250
Cubical sheaves 80 81
Curvature 185 186
Cuspidal group 128
Cuspidal group, ideal 129
Cusps 127
Cycles 31 32 254
Cyclotomic character 133
Cyclotomic extensions 29 247
Cyclotomic units 141
d(F) or d(P) 55
Davenport 48 49 247
de Franchis theorem 13 24
De Rham cohomology 153Ч160
Decomposition group 83 88 112
Degree of canonical sheaf 152
Degree of divisor on a curve 9
Degree of hypersurface 4
Degree of isogeny 35
Degree of line sheaf 144
Degree of metrized line sheaf 116
Degree of polarization 35
Degree on a singular curve 144
Degree with respect to Riemann form 238 (see also УIsogenyФ УPolarizationФ)
Degree, Arakelov 168
Deligne on Faltings proof 120
Deligne on L-function 92
Deligne Ч Mumford 150
Deligne Ч Serre representation 132
Demjanenko Ч Manin on split function field case 79
Demjanenko, estimate of Neron height 72
Demjanenko, fibering of Fermat surface 23
Descent 85 90 91 160 219
Descent in coverings 160 219
Descent with Selmer groups 90
Determinant of vector sheaf 144
Diagonal hyperplane 183
Different 120
Differential form 10
Differentials 115
Differentials of first kind 11 136
DIMENSION 4
Diophantine approximation on toruses 233Ч243
Diophantine approximation to numbers 213Ч216
Dirichlet box principle 234
Discriminant 50 55 69
Discriminant in coverings 224
Discriminant of elliptic curve 69 96
Distance 177
Division group 37 38 161 Raynaud
Divisor 6
Divisor class group 6 33
Divisor classes and heights 58Ч61 194Ч196
Divisor classes and Neron functions 213
Dobrowolski 243
Dolbeault operator 172
Dual variety 33
DysonТs lemma 229 231 232
Effective divisor 6
Effective divisor class 7
Eigenform 131 132
Eigenvalues of Frobenius 85 91 131
Eigenvalues of Laplacian 173 175
Eisenstein ideal 129
Eisenstein ideal, quotient 129
Eisenstein ideal, series 260
Elkies example of integral points 50
Elkies on Fermat hypersurface 23
Elliptic curve 12 21 23 25Ч27 49 50 96 132 135 139Ч142 162
Elliptic curve, conductor 97 98
Elliptic curve, diophantine approximation 235 236
Elliptic curve, fibers of family 21 23
Elliptic curve, Frey 132 135
Elliptic curve, height of generators 99 100
Elliptic curve, integral points 50
Elliptic curve, isomorphism 96
Elliptic curve, L-function 97Ч98 137Ч142
Elliptic curve, minimal discriminant 97
Elliptic curve, modular 130Ч142
Elliptic curve, periods 93 95 97 125 236
Elliptic curve, rank 28 42 92 139Ч142
Elliptic curve, rank one over the rationals 137Ч142
Elliptic curve, Tate curve 162 (see also УTorsion pointsФ)
Error function in Nevanlinna theory 203 224
Error terms in second main theorem 199Ч204 224
Error terms in second main theorem, Lang conjecture 200
Esnault Ч Viehweg inequality 152
Esnault Ч Viehweg inequality on Roth theorem 229
Euler characteristic 172
Euler characteristic, arithmetic 173
Euler on Fermat 22
Euler product for a variety 91
Exact sequence, de Rham cohomology 156
Exact sequence, group cohomology 88 250 255
Exact sequence, Lang Ч Tate 87
Exact sequence, Selmer and Shafarevich Ч Tate group 88Ч90
Exceptional set in Vojta conjecture 67
Exceptional set in Vojta conjecture in Schmidt Ч Vojta theorem 215 222
Exponential on Lie groups 236
Faltings, canonical height 119
Faltings, finiteness of l-adic representations 114
Faltings, finiteness of rational points 12 18 36 230 232
Faltings, formula for the degree 120
Faltings, height 74 117Ч123 238
Faltings, inequality on abelian varieties 220 237
Faltings, integral points on abelian varieties 220 221
Faltings, positivity of canonical sheaf 170
Faltings, semisimplicity and Tate conjecture 111Ч115
Faltings, stable height 117 238
Faltings, subvariety of abelian variety 36
Fano variety 260
Fermat 11 22 23 48 62 64 132 135 181 225
Fermat, Brody Ч Green perturbation 181
Fermat, curve 11
Fermat, Euler 22
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



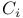 property
property 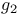 and
and 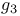
 -degree
-degree 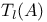
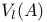
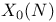
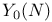 and
and 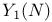
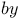 X_1(N)$
X_1(N)$