|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Нагумо М. — Лекции по современной теории уравнений в частных производных |
|
|
 |
| Предметный указатель |
(—k)-норма 102
K-норма 101
Агмон (Agmon, S.) 87
Агранович, М.С. 97
Ахиезер, Н.И. 9 24 86
Банах (Banach, S.) 17
Бартл (Bartle, R.G.) 87
Бейд (Bade, W.G.) 87
Березанский, Ю.М. 87
Берс (Bers L.) 6 87
Браудер (Browder, F.E.) 87
Вишик, М.И. 66 87 124
Галахов, М.А. 122
Гарабедян (Garabedian, P.R.) 124
Гельфанд, И.М. 122 124
Гильберт (Hilbert, D.) 123
Глазман, И.М. 9 24 86
Гординг (Garding, L.) 122 123
График оператора 20
Данфорд (Dunford, N.) 86 87
Дафф (Duff) 123
Дезин, А.А. 122
Джон (John, F.) 6 87 122
Дирихле (Dirichlet, L.) 56 62—65 86
Дифференциальные свойства решений задачи Коши для симметричных гиперболических систем 116 118
Дифференциальные свойства решений симметричных гиперболических систем 108 111
Дифференциальные свойства решений эллиптических уравнений 77 85
Дуглис (Duglis, A.) 87
Единственность обобщенного решения у симметричных гиперболических систем 96
Единственность решения задачи Дирихле 68
Единственность решения задачи Коши для симметричных гиперболических систем 99
Задача Дирихле 63
Задача Дирихле обобщенная 63
Задача Коши 99
Замыкание 21
Интегральное представление функции 82
Интегральное энергетическое неравенство 96
Иосида (Yosida, K.) 25 122 124
Като (Kato, T.) 124
Котаке (Kotake, S.) 122
Коши (Cauchy, A.) 88 94 122
Курант (Courant, R.) 123
Ладыженская, О.А. 124
Лаке (Lax, P.D.) 7 55 56 66.67 85 88 121 122
Лаплас (Laplace, P.S.) 89
Лебег (Lebesgue, H.) 10
Леви (Lewy, H.) 87 124
Лемма Лакса — Мильграма 66
Лере (Leray, J.) 122
Линейный функционал 16
Лионе (Lions, J.L.) 14
Локальное свойство дифференциальных операторов 36
Люстерник, Л.А. 9 86
Маслов, В.П. 122
Мильграм (Milgram, A.N.) 56 66 85
Мимура (Mimura, Y.) 24
Миранда (Miranda, C.) 87
Михлин, С.Г. 87
Нагумо (Nagumo, M.) 121
Неравенство Шварца 12
Неравенство Шварца, обобщенное 103
Ниренберг (Nirenberg, L.) 87
Норма 11 13
Норма в пространстве ![$C^k[G]$](/math_tex/a31322524f93d1d3724c52280c99152c82.gif) 16 16
Норма в пространстве ![$L^p[G]$](/math_tex/93a7cac283970039c7d0183697f8597a82.gif) 57 57
Норма в пространстве ![$\mathfrak{D}[G]$](/math_tex/5b71abba63d218686e9b4754a418262f82.gif) 11 11
Норма в пространстве С[G] 14
Норма функционала 17
Носитель функции 10
Область влияния 119
Область зависимости решения от начальных данных 119
Обобщенная задача Дирихле 63
Обобщенное неравенство Шварца 103
Оператор 14
Оператор 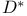 63 63
Оператор  57 57
Оператор 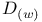 57 57
Оператор 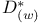 62 62
Оператор d 57
Оператор дифференциальный 26
Оператор дифференциальный  104 104
Оператор дифференциальный 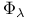 96 96
Оператор дифференциальный матричный первого порядка 29 30
Оператор дифференциальный матричный первого порядка формально сопряженный 31
Оператор дифференциальный формально самосопряженный 27
Оператор дифференциальный формально сопряженный 28
Оператор замкнутый 20
Оператор замкнутый в пространстве ![$\mathfrak{L}^p[G]$](/math_tex/f9a02e771d9c410616e0345dbc4e807f82.gif) 23 23
Оператор замыкаемый 20
Оператор интегральный 15 37
Оператор интегральный скалярный 48
Оператор интегральный сопряженный 38
| Оператор Лапласа 89
Оператор линейный 14
Оператор неограниченный 20
Оператор непрерывный 15
Оператор ограниченный 14
Оператор осреднения 39 48
Ортогональность 18
Петровский, И.Г. 122 123
Планшерель (Plancherel, M.) 108
Плотное множество 12
Полная непрерывность 71
Принцип Дирихле 86
Пространство ![$(C^k[G])^l$](/math_tex/838b4260d3e23635eb5d7566a075fffe82.gif) 29 29
Пространство ![$(C^{\infty}[G])^l$](/math_tex/0c6f997dc870be86be0925bbb5672b5082.gif) 33 33
Пространство 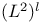 46 46
Пространство 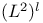 33 33
Пространство ![$C^k[G]$](/math_tex/a31322524f93d1d3724c52280c99152c82.gif) 9 9
Пространство ![$C^{k}_0[G]$](/math_tex/58a235760a19f28f6e33d055a283ad8482.gif) 10 10
Пространство ![$C^{\infty}[G]$](/math_tex/2a34f4e4ade86b601212efd750d8091d82.gif) 9 9
Пространство ![$C^{\infty}_0[G]$](/math_tex/5dd99570c527de2316416a89a4df9f7b82.gif) 10 10
Пространство ![$C_{0}[G]$](/math_tex/58ced1300b993b0f31d8ba50ced5c9ab82.gif) 10 10
Пространство  10 10
Пространство ![$\mathfrak{D}*[G]$](/math_tex/3fb0d56b24bf5ae3c492d9c4ce4376cc82.gif) 63 63
Пространство ![$\mathfrak{D}[G]$](/math_tex/5b71abba63d218686e9b4754a418262f82.gif) 57 57
Пространство ![$\mathfrak{D}^k[G]$](/math_tex/fc870b4c731752e9c67360a87f66a50382.gif) 101 101
Пространство ![$\mathfrak{D}^k[G]$](/math_tex/fc870b4c731752e9c67360a87f66a50382.gif) ' 115 ' 115
Пространство ![$\mathfrak{D}^k_0[G]$](/math_tex/f91aebed5c7c206101f69afbe95db01082.gif) 101 101
Пространство ![$\mathfrak{D}^{-k}[G]$](/math_tex/54876358584d1097f04c144af8f83d4882.gif) 110 110
Пространство ![$\mathfrak{D}_0[G]$](/math_tex/abde65947a190b1c0bd6c97fdbd60f8f82.gif) 58 58
Пространство ![$\mathfrak{F}^{(l)}_{s}[G]$](/math_tex/9b9c281c5dc31c7b94982b6066b16f8682.gif) 33 33
Пространство ![$\mathfrak{F}^{l}_{(w)}[G]$](/math_tex/181ba9b18d4f1d3e4066d629a0be872382.gif) 35 35
Пространство ![$\mathfrak{F}_{(s)}[G]$](/math_tex/90f3613af8cbb9a725c1bf18aa51fa5c82.gif) 32 32
Пространство ![$\mathfrak{F}_{(w)}[G]$](/math_tex/760243bf9db5c7414660694cac3b5d9182.gif) 34 34
Пространство ![$\mathfrak{F}_{\varphi}[G]$](/math_tex/4e8e68a1b0bdf83f98d713d8bd31c36482.gif) 97 97
Пространство ![$\mathfrak{L}^p[G]$](/math_tex/f9a02e771d9c410616e0345dbc4e807f82.gif) 21 22 21 22
Пространство C[G] 9
Пространство банахово 14
Пространство векторное 13
Пространство векторное действительное 13
Пространство векторное комплексное 13
Пространство гильбертово 16
Пространство линейное 13
Пространство метрическое 11
Пространство нормированное 13
Пространство полное 11 14
Пространство сопряженное 17
Равномерная непрерывность 40 52
Равномерная сходимость 14
Радо (Rado, T.) 87
Расстояние 11 13 14
Регулярные гиперболические уравнения 90
Риман (Riemann, B.) 122
Рисе (Riesz, F.) 7 9 18 24 56 57 66 69 74 75 85 86 93
Саразон (Sarason, L.) 55 122
Секефальви-Надь (Sz-Nagy, B.) 9 24 86
Сильное расширение дифференциального оператора 32
Сильное расширение матричного дифференциального оператора первого порядка 33
Симметричные гиперболические системы уравнений 91
Симметричные системы уравнений 91
Скалярное (внутреннее) произведение 12 18 26 30 58 95 101
Слабая сходимость 24
Слабое расширение дифференциального оператора 34
Слабое расширение матричного дифференциального оператора первого порядка 35
Соболев, В.И. 9 86
Соболев, С.Л. 5 56 81 84 86 87 108 111 122 124
Совпадение слабого и сильного расширений для дифференциальных операторов с постоянными коэффициентами 44 45
Совпадение слабого и сильного расширений для матричных дифференциальных операторов первого порядка с переменными коэффициентами 53
Существование обобщенного решения симметричных гиперболических систем 94
Существование решения задачи Дирихле 65 68
Существование решения задачи Коши для симметричных гиперболических систем 99
Теорема Рисса об общем виде линейного функционала 18 93
Теорема Соболева 84
Теорема Хана — Банаха 17
Трев (Treves, J.) 124
Филлипс (Phillips, R.S.) 55 122
Фредгольм (Fredholm, I.) 69
Фридрихе (Friedrichs, K.O.) 5 7 25 36 54 56 86 88 121 122
Фундаментальная последовательность 11
Фурье (Fourier, J.B.J.) 87 89 107 108 123 124
Хан (Hahn, H.) 17
Хёрмандер (Hormander, L.) 55 123 124
Шаудер (Schauder, J.) 57 69 74
Шварц, Г. (Schwarz, H.A.) 12 72 103 110
Шварц, Дж. (Schwartz, J.T.) 86 87
Шварц, Л.(Schwartz, L.) 124
Шехтер (Schechter, M.) 6 87
Шилов, Г.Е. 122 124
Эллиптические дифференциальные операторы 64
Энергетическое неравенство 96
Эскин, Г.И. 87
Ядро 37
Ядро матричное 46
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



![$C^k[G]$](/math_tex/a31322524f93d1d3724c52280c99152c82.gif)
![$L^p[G]$](/math_tex/93a7cac283970039c7d0183697f8597a82.gif)
![$\mathfrak{D}[G]$](/math_tex/5b71abba63d218686e9b4754a418262f82.gif)
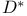

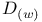
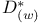

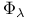
![$\mathfrak{L}^p[G]$](/math_tex/f9a02e771d9c410616e0345dbc4e807f82.gif)
![$(C^k[G])^l$](/math_tex/838b4260d3e23635eb5d7566a075fffe82.gif)
![$(C^{\infty}[G])^l$](/math_tex/0c6f997dc870be86be0925bbb5672b5082.gif)
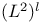
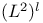
![$C^{k}_0[G]$](/math_tex/58a235760a19f28f6e33d055a283ad8482.gif)
![$C^{\infty}[G]$](/math_tex/2a34f4e4ade86b601212efd750d8091d82.gif)
![$C^{\infty}_0[G]$](/math_tex/5dd99570c527de2316416a89a4df9f7b82.gif)
![$C_{0}[G]$](/math_tex/58ced1300b993b0f31d8ba50ced5c9ab82.gif)

![$\mathfrak{D}*[G]$](/math_tex/3fb0d56b24bf5ae3c492d9c4ce4376cc82.gif)
![$\mathfrak{D}^k[G]$](/math_tex/fc870b4c731752e9c67360a87f66a50382.gif)
![$\mathfrak{D}^k_0[G]$](/math_tex/f91aebed5c7c206101f69afbe95db01082.gif)
![$\mathfrak{D}^{-k}[G]$](/math_tex/54876358584d1097f04c144af8f83d4882.gif)
![$\mathfrak{D}_0[G]$](/math_tex/abde65947a190b1c0bd6c97fdbd60f8f82.gif)
![$\mathfrak{F}^{(l)}_{s}[G]$](/math_tex/9b9c281c5dc31c7b94982b6066b16f8682.gif)
![$\mathfrak{F}^{l}_{(w)}[G]$](/math_tex/181ba9b18d4f1d3e4066d629a0be872382.gif)
![$\mathfrak{F}_{(s)}[G]$](/math_tex/90f3613af8cbb9a725c1bf18aa51fa5c82.gif)
![$\mathfrak{F}_{(w)}[G]$](/math_tex/760243bf9db5c7414660694cac3b5d9182.gif)
![$\mathfrak{F}_{\varphi}[G]$](/math_tex/4e8e68a1b0bdf83f98d713d8bd31c36482.gif)