|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Lipschutz Seymour Ч Schaum's Outline of Theory and Problems of Linear Algebra (Schaum's Outlines) |
|
|
 |
| ѕредметный указатель |
 52Ч53 72 52Ч53 72
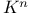 142 142
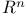 40Ч41 53Ч54 40Ч41 53Ч54
Absolute value 52
Adjoint operator 425Ч426 433Ч436
Adjoint operator, matrix representation 426
Adjoint, classical 253Ч254
Algebra of linear maps 322
Algebraic multiplicity 285
Algorithm, basis-finding 154
Algorithm, determinant 253
Algorithm, diagonalization under, congruence 102Ч104
Algorithm, diagonalization under, similarity 102 286
Algorithm, Elimination (Gaussian) 8 24Ч25 100 261
Algorithm, Euclidean 446
Algorithm, Gauss Ч Jordan 29
Algorithm, inverse matrix 100
Algorithm, orthogonal diagonalization 289
Alternating bilinear form 411
angle 45 206
Annihilators 399Ч400 403Ч404
Arbitrary permutations 249
Augmented matrix 78
A{V) 322
B(V) 409
Back-substitution 9
Basis, dual 398 400Ч403
Basis, general solution 19Ч20
Basis, orthogonal 208
Basis, second dual 399
Basis, usual 150
Basis, vector space 150 169Ч171
Basis-finding algorithm 154
Bessel inequality 212
Bijective mapping 314
Bilinear form 409 414Ч416
Bilinear form, alternating 411
Bilinear form, Bilinear form, polar form of 412
Bilinear form, matrix representation of 410
Bilinear form, rank of 411
Bilinear form, real symmetric 412Ч413
Bilinear form, symmetric 411Ч412
Block matrix 79Ч80 86
Block matrix, determinant of 256Ч257
Block matrix, diagonal 98 291
Block matrix, Jordan 374
Block matrix, square 98 123Ч124
Block matrix, triangular 98
Cancellation law 142
Canonical form 14 352
Canonical form, Jordan 373Ч374 381Ч385
Canonical form, rational 375Ч376 388Ч390
Canonical form, row 14 16 28Ч30
Cauchy Ч Schwarz inequality 45 58 205Ч206 218
Cayley Hamilton theorem 282 302Ч304 307
cells 79
Change of basis 159Ч162 187Ч191
Change-of-basis matrix 160 348 357Ч359
Change-of-variable matrix 105Ч106
Characteristic polynomial 281Ч284 349
Classical adjoint 253Ч254
Codomain 312
Coefficient 1
Coefficient matrix 17 78
Coefficient, Fourier 211
Cofactor 252
column 13 74
Column, operations 100Ч102
Column, rank 152
Column, space 146
Column, vector 40 75
Commuting matrices 90
Companion matrix 291 375
Complement, orthogonal 207Ч208 226
Complex, conjugate 51
Complex, inner product 216Ч218
Complex, matrix 96 121Ч122
Complex, n-space 52
Complex, numbers 51
Component 40 211
Composition of mappings 313
Congruent, diagonalization 102Ч103
Congruent, matrices 102 410
Congruent, symmetric matrices 102Ч103 124Ч125
Conjugate matrix 96
Conjugate, complex 51
Consistent systems 13
Convex set 342 407
Coordinate vector 157 186Ч187
coordinates 40 157Ч159
cosets 376
Cramer's rule 255 263Ч264 268
Cross product 49Ч50 65Ч67
CURVES 48
Cyclic subspaces 374Ч375 388Ч389
Degenerate linear equations 2 3
Degree of polynomial 446
Dependence, linear 147 166Ч169
Determinant 246
Determinant, block matrix 256Ч257
Determinant, computation of 253 260Ч262
Determinant, linear equations 254Ч255
Determinant, linear operators 349
Determinant, multiplinearity 257Ч258
Determinant, order 3 248
Determinant, order n 250
Determinant, properties 251Ч252
Determinant, volume 257
Diagonal (of a matrix) 90
Diagonal matrix 93Ч94
Diagonal matrix, block 98
Diagonalizable matrices 280 288Ч289 298Ч301
Diagonalization 349Ч350 360Ч363
Diagonalization algorithm 102Ч104 286Ч288
Dimension of solution spaces 19
Dimension of vector spaces 150Ч151
Dimension of vector spaces, subspaces 151 171Ч172
Direct sum 156 181Ч186
Direct sum, decomposition 371 379Ч380
Directed line segment 46
Distance 45
Domain 312
Dot product 43Ч46 52 56Ч57
Dual basis 398
Dual space 397
Echelon form 10Ч11 14 23Ч24
Echelon matrices 14
Eigenvalue 284Ч285 292Ч298 350
Eigenvalue, computing 286Ч287
Eigenvector 284Ч286 292Ч298 350
Eigenvector, computing 286Ч287
Elementary divisors 376
Elementary matrix 99 101 117Ч118
Elementary operations 7Ч8
Elementary operations, column 100Ч102
Elementary operations, row 14 98Ч100
Elimination algorithm 6
Elimination, Gaussian 8 24Ч26 100 261
Enenspace 284 350
Equal matrices 74
Equal vectors 40
Equations See Linear equations
Equivalence, matric 100 102
Equivalence, row 14 16
Equivalent systems 7Ч8
Euclidean algorithm 446
Euclidean space 203
Evaluation map 92
Factorization, LU 109Ч111 130Ч133
Factorization, polynomial 448
| Field 74
Finite dimension 150Ч151
Fourier coefficient 211
Free variable 3 10
Function, spaces 143
Function, square matrix 89Ч90
Functional, linear 397
F{X) 143
Gauss Ч Jordan algorithm 29
Gaussian elimination 8 24Ч26 100 261
General solution 1 7
Geometric multiplicity 285
Gram Ч Schmidt orthogonalization 213
Graph 4
Greatest common divisor 447
Hermitian form 413Ч414
Hermitian matrix 97
Hermitian quadratic form 414
Hilbert space 205
Homogeneous systems 18Ч20 32Ч34 399Ч400
Hyperplane 46 407
Identity mapping 314
Identity matrix 91
ijk notation 49
Im F 316
Im z 51
Image of linear mapping 316Ч318 328Ч331
Imaginary part 51
Inconsistent systems 13
Independence, linear 147Ч150
Infinite dimension 150
Infinity-norm 219
Injective mapping 314
Inner product 202 221Ч226
Inner product spaces 202Ч205
Inner product spaces, linear operators on 425
Inner product, complex 216Ч218
Inner product, usual 203 214Ч216 218
Invariance 370Ч371
Invariant subspaces 370Ч371 377Ч378
Inverse matrix 92
Inverse matrix, computing algorithm 100
Invertible matrices 92Ч93 115Ч117
Invertible matrices, linear substitutions 105
Invertible matrices, operators 323
Isomorphic vector spaces 316
Isomorphism 158Ч159 316 320
Jordan block 374
Jordan canonical form 373Ч374
Ker F 316
Kernel of a linear map 316Ч320 328Ч332
Kronecker delta 91
Laplace expansion 252
Law of inertia 102 413
Leading nonzero entry 13
Leading unknown 3
Length 44 203
Line 47
linear combination 19 41Ч42 145Ч147 149 165Ч166
Linear dependence 42Ч43 147Ч149 166Ч169
Linear equation 1
Linear equation, degenerate 2Ч3
Linear equation, one unknown 2
Linear equations (system) 1 21 152Ч153 319Ч320 323Ч324 399Ч400
Linear equations (system), consistent 13
Linear equations (system), echelon form 10 23Ч24
Linear equations (system), triangular form 9Ч10 23
Linear equations (system), two unknowns 4Ч6
Linear functional 397 426Ч427
Linear independence 43 147Ч149
Linear mapping 314Ч316 319 326Ч328
Linear mapping, image 316Ч319 328Ч331
Linear mapping, kernel 316Ч320 328Ч332
Linear mapping, matrix representation 351
Linear mapping, nullity 318Ч319
Linear mapping, rank 318Ч319
Linear mapping, transpose 400
Linear operator 322
Linear operator, adjoint 425
Linear operator, characteristic polynomial 349
Linear operator, determinant 349
Linear operator, inner product spaces 425
Linear operator, invertible 323
Linear operator, matrix representation 344
Linear operator, nilpotent 373
Linear span 145
Located vectors 46
LU factorization 109Ч111 130Ч133
Mappings (maps) 312Ч314 324Ч326
Mappings (maps), composition of 313
Mappings (maps), linear 314Ч316 326Ч328
Matrices 13Ч14 74Ч75
Matrices, augmented 78
Matrices, block 79Ч80 86
Matrices, change-of-basis 160 348 430
Matrices, change-of-variable 105Ч106
Matrices, coefficient 17 78
Matrices, companion 375
Matrices, complex 96Ч97
Matrices, diagonal 93Ч94
Matrices, diagonizable 280 298
Matrices, echelon 14
Matrices, equivalent 102
Matrices, invertible 92Ч93
Matrices, nonsingular 92Ч93
Matrices, normal 97
Matrices, similar 357Ч359
Matrices, square 89Ч90
Matrices, triangular 94
Matrix representation, adjoint operator 426
Matrix representation, bilinear form 410Ч411
Matrix representation, linear maps 344 351 363Ч365
Matrix representation, quadratic form 104
Matrix space 142
Minimum polynomial 289Ч291 301Ч303 351
Minkowski's inequality 45
Minor 252 255Ч256
Minor principle 256
Monic polynomial 282 446
Multilinearity 257Ч258
Multiplication of matrices 76Ч77
Multiplicity 285
Multiplicity, n-space 40
Nilpotent 373
Nondegenerate linear equations 3
Nonnegative semidefinite 413
Nonsingular linear maps 320
Nonsingular matrices 92- 93
Norm 44 57Ч59 203 219Ч220 238
Normal matrix 97
Normal operator 428 432
Normal vector 46
Normalizing 44
Normed vector spaces 219Ч221
Nullity 318Ч319
One-norm 219Ч220
One-to-one correspondence 314
One-to-one mapping 314
Onto mapping 314
Operations on linear maps 320Ч321
Operators See Linear operators
Orthogonal basis 209
Orthogonal complement 207Ч208 226
Orthogonal matrix 95 216 429Ч430
Orthogonal operator 427Ч429 431Ч432
Orthogonal projections 433
Orthogonal sets 208Ч209 212
Orthogonality 43 226Ч229 280
Orthogonalization (Gram Ч Schmidt) 213
Orthonormal basis 209
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте