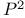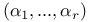|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Miyahishi M. — Non-complete Algebraic Surfaces |
|
|
 |
| Предметный указатель |
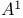 -bundle I.4.8.5 -bundle I.4.8.5
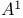 -cylinder I.2.2 -cylinder I.2.2
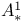 -bundle I.4.8.5 -bundle I.4.8.5
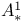 -cylinder II.5.1 -cylinder II.5.1
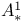 -cylinder, twisted II.5.1 -cylinder, twisted II.5.1
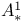 -fiber space I.5.1 -fiber space I.5.1
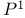 -bundle Introduction -bundle Introduction
Action of I.4.6
Addition formula of Kodaira dimension I.1.6
Additive group scheme 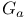 I.4.6 I.4.6
Albanese mapping, Albanese variety I.2.3.2
Boundary curve I.4.4.2
Branch point II.2.3.2
Canonical model Introduction
Component of a divisor, adjacent III.2.4.1
Component of a divisor, arithmetically effective I.3.1
Component of a divisor, arithmetically negative I.3.1
Component of a divisor, connected I.2.1.2
Component of a divisor, horizontal II.2.3.2
Component of a divisor, irreducible I.2.1.2
Component of a divisor, isolated I.2.4.1
Component of a divisor, pseudo-effective I.3.1
Component of a divisor, terminal I.2.4.1
Continued fraction I.6.6
Contraction, blowing down I.2.6.4
Cross-section I.2.4.1
Curve with only one place at infinity I.6.3
Cusp I.2.7.2
CYCLE I.2.1.2
Cylinderlike open set I.2.2
Dimension, (ordinary) Kodaira I.1.1
Dimension, D-dimension I.1.1
Dimension, logarithmic Kodaira I.1.3
Diophantine equation I.4.7.1
Diophantine equation, constant solution of I.4.7.1
Diophantine equation, non-constant solution of I.4.7.1
Divisor, canonical Introduction
Divisor, divisor of quasi-canonical type II.3.1
Divisor, effective, strictly effective I.2.1
Divisor, indecomposable II.3.1
Divisor, integral I.3.11
Divisor, reduced I.2.1
Divisor, support of I.2.1.2
Divisorial cycle, Q-divisor I.3.1
Divisorial cycle, Q-divisor, arithmetically effective I.3.1
Divisorial cycle, Q-divisor, integral part of II.1.5
Divisorial cycle, Q-divisor, pseudo-effective I.3.1
Dual graph I.2.1.2
Elliptic bundle Introduction
Exceptional curve of the first kind I.2.2
Fiber, general I.4.5.3
Fiber, generic II.5.1
Fiber, multiple fiber I.4.7 1.5.1
Fiber, multiplicity of I.4.7
Fiber, singular fiber I.4.7 1.5.1
Fiber, singular fiber of the first kind I.4.7
Fiber, singular fiber of the second kind I.4.7
Fibration, 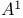 -fibration I.4.3 -fibration I.4.3
Fibration, 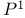 -fibration I.5.1 -fibration I.5.1
Fibration, elliptic II.2.3.1
Fibration, quasi-elliptic II.2.3.2
Fibration, relatively minimal II.3.4
Fundamental cycle III.2.1
Genus, arithmetic genus of a curve Notations
Genus, geometric genus of a curve I.2.3.1
Genus, geometric genus of a surface II.3.4
| Genus, logarithmic plurigenus I.1.3
Genus, plurigenus Notations
Hirzebruch surface I.2.6.3
Infinitely near point I.2.4.1
Intersection matrix, negative definite I.3.1
Intersection matrix, negative semi-definite I.3.4
Intersection number, multiplicity Notations
Intersection number, multiplicity, self-intersection Notations
Irregularity I.2.1.1
Line, affine line 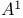 , projective line , projective line 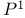 Notations Notations
Linear chain I.2.7
Linear equivalence Notations
Linear system I.1.1
Linear system, base point of I.2.2
Linear system, canonical, pluricanonical Introduction
Linear system, complete I.1.1
Linear system, fixed part of II.3.4
Linear system, movable part of II.3.4
Locally nilpotent derivation I.4.6.2
Loop I.2.1.2 III.2.3
Model, canonical Introduction
Model, quasi-canonical III.1.1
Model, relatively minimal model of (V,D) II.2.1
Morphism, canonical, pluricanonical Introduction
Morphism, dominant I.1.3
Morphism, pluri-quasicanonical III.1.2
Multiplicative group scheme 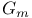 I.4.8.1 I.4.8.1
Multiplicative group scheme 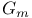 , action of I.4.8.1 , action of I.4.8.1
Multiplicity sequence of a singular point I.5.7
Node I.2.7.2
Normal compactification I.1.3
Normal crossings as singularities I.1.2
Numerical equivalence I.3.10
Numerically independent I.3.6
Pencil, algebraic I.2.2
Pencil, linear Notations
Plane, affine plane 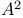 , projective plane , projective plane 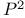 Notations Notations
Pluri-quasicanonical ring II1.1.7
Polynomial ring I.4.1
Quadratic form associated with a Q-divisor I.3.1
Quadratic transformation, blowing up 1.2.2
Rational double point III.2.1
Regular ring I.4.1
Resolution, minimal I.6.2
Resolution, minimal good I.6.2
Riemann-Hurwitz theorem I.2.3.1
Riemann-Roch theorem I.2.4.1
Section, cross-section I.2.4.1
Section, minimal I.2.6.3
Singular point, cyclic quotient I.6.6
Singular point, isolated I.6.2
Singular point, rational III.2.1
Singular point, rational singular point of type 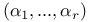 I.6.6 I.6.6
Singular point, simple elliptic III.3.1
Singular point, simple quasi-elliptic III.3.1
Standard process II.1.3
Standard process, transcendental II.1.6.3
Surface, elliptic Introduction
Surface, rational I.2.4
Surface, relatively minimal I.2.6.3
Surface, ruled I.2.3.2
Surface, surface of general type Introduction
Torsion part of the Picard group I.4.7.3
Transform, proper, total Notations
TREE I.2.3.1
Unique factorization domain I.4.1
Zariski decomposition I.3.1
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



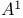 -bundle
-bundle 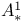 -bundle
-bundle 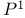 -bundle
-bundle 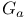
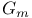
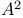 , projective plane
, projective plane