|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Mielke A. — Hamiltonian and Lagrangian Flows on Center Manifolds: With Applications to Elliptic Variational Problems |

Обсудите книгу на
Нашли опечатку?
Выделите ее мышкой и нажмите Ctrl+Enter
|
Название: Hamiltonian and Lagrangian Flows on Center Manifolds: With Applications to Elliptic Variational Problems
Автор: Mielke A.
Язык: 
Рубрика: Математика/
Статус предметного указателя: Готов указатель с номерами страниц
ed2k:
Год издания: 1991
Количество страниц: 140
Добавлена в каталог: 18.08.2008
Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
|
|
 |
| Предметный указатель |
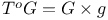 76 76
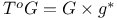 50 50
Action of a Lie group 42
Action, (co-) adjoint 42
Action, infinitesimal adjoint 78
Action, lifted 49
Augmented Hamiltonian 82
Canonical Hamiltonian system 49
Canonical symplectic form 11
Center manifold 14
Center manifold, analyticity of 38
Center manifold, flattening of 34
Center manifold, reduction 14
Center space 14 19
Cross-section 96
Darboux’s Theorem for nonautonomous systems 87
Darboux’s Theorem, close to a submanifold 55
Darboux’s Theorem, G-invariant 54
Direct product  44 44
Ellipticity (strong) 97 111
Euclidian transformations 44 123
Euler — Lagrange equation 96
Exponential function 42
Extended phase space 86
Exterior derivative 11
Fiber derivative 65
Frame indifference 122
G invariant 43
Galerkin method 64
Generating function 36
Gradient flow 63
Hamiltonian system 12
Hamiltonian system, generalized 13
Hyperelastic, material (beam) 122
Hyperelastic, rod 126
Invariant submanifold 13
Isotropic submanifold 12
Lagrange equation 65
Lagrangian flow 67
Legendre transformation 66
Lie algebra 41
Lie bracket of vector fields 10
Lie bracket on the Lie algebra 41
Lie group 41
Lie — Poisson bracket 78
| Linear representation 42
Lyapunov — Schmidt reduction 62
Manifold, domain 10
Manifold, infinite dimensional 9
Natural reduction 73
Natural reduction, relaxed 74
Necking 109
Nonautonoxnous systems 85
Normal forms (linear) 20
Orbit  44 44
Orthogonal complement 12
Poincare’s Lemma, close to a submanifold 54
Poincare’s Lemma, G-invariant 53
Poisson bracket 12
Projection method 64
Pull back 52
Rank-one convexity 97
Reduced equation 14
Reduced, equation 27
Reduced, Hamiltonian 28
Reduced, Poisson structure 33
Reduced, symplectic structure 28
Reduction by symmetry 43
Reduction of gradient systems 63
Reduction of Lagrangian systems 72
Reduction of variational problems 61
Reduction, function 14
Relative equilibrium 77
Reversible 57
Rigid-body transformation 123
Rod equations 129
Saint — Venant’s principle 96
Saint — Venant’s problem 121
Slice theorem (G-invariant) 45
Spectral projection 18
Stored energy function 109 122
Strain tensor 122
Stress tensor 122
Symplectic 11
Symplectic, basis 51
Symplectic, submanifold 12
Tangent space 9
Translation left/right 41
Water waves, internal 101
Water waves, surface 103
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте