|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hirschfeld J., Wheeler W.H. Ч Forcing, Arithmetic, Division Rings |
|
|
 |
| ѕредметный указатель |
 , ,  31 see 31 see
 160 160
 89 see finite also 89 see finite also
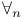 -extension of a structure 104Ч107 -extension of a structure 104Ч107
 16Ч17 see 16Ч17 see
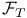 96 see finitely also 96 see finitely also
 57 see infinitely also 57 see infinitely also
 -equivalence, -equivalence,  -substructure, -substructure,  -equivalence, -equivalence,  -substructure 9 -substructure 9
 -equivalence, -equivalence,  -substructure, -substructure,  -equivalence, -equivalence,  -substructure, for existentially complete division algebras 215Ч216 -substructure, for existentially complete division algebras 215Ч216
 -equivalence, -equivalence,  -substructure, -substructure,  -equivalence, -equivalence,  -substructure, for existentially universal structures 42Ч43 -substructure, for existentially universal structures 42Ч43
 -equivalence, -equivalence,  -substructure, -substructure,  -equivalence, -equivalence,  -substructure, for regular models of arithmetic 162 -substructure, for regular models of arithmetic 162
 236 see second also 236 see second also
 168 see second also 168 see second also
 , ,  72Ч73 see also 72Ч73 see also
Algebraically closed structures 1Ч2 13 15 224
Amalgamation of division algebras 196Ч197
Amalgamation property 50Ч51
Analytical hierarchy 117Ч131 184Ч186 241Ч252
Approximating chains 76Ч85
Approximating chains in arithmetic 182Ч186
Approximating chains in division algebras 244Ч247 250Ч252
Approximating chains, 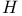 chain 81Ч83 121Ч124 125Ч126 chain 81Ч83 121Ч124 125Ч126
Approximating chains,  chain 83Ч85 121Ч124 125Ч126 chain 83Ч85 121Ч124 125Ч126
Approximating chains, Cherlin chain 77Ч80
Approximating theories for  104Ч110 124Ч125 104Ч110 124Ч125
Arithmetic, existentially complete models of 141 146Ч154 155Ч189
Arithmetic, existentially complete models of, Biregular models 140 165Ч170 172Ч178 179
Arithmetic, existentially complete models of, Existentially universal models 179Ч181
Arithmetic, existentially complete models of, Finitely generic models 188
Arithmetic, existentially complete models of, Infinitely generic models 179Ч181
Arithmetic, existentially complete models of, Regular models 6 139 160Ч165 168Ч172 180
Arithmetic, existentially complete models of, Simple models 6 139 155Ч159
Arithmetic, models of, Nonstandard 141
Arithmetic, models of, Standard 141
Arithmetic, second order, 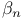 -models 182Ч186 -models 182Ч186
Arithmetic, second order, Interpretations of 168Ч169 236Ч240 241Ч252
Arithmetic, second order, Models of arithmetical comprehension 173Ч178
Arithmetic, second order, Structures for 168Ч186 233Ч236
Automorphisms of existentially complete division algebras 199Ч202 218Ч219
Automorphisms of existentially complete models of arithmetic 158 165
Center of a division ring 194
Centralizer in a division algebra 200Ч202 207Ч214 216Ч217
Characteristic of a division ring 194
Compactness Theorem 10
Complete type 41
Completeness theorem 10
Condition (for finite forcing) 87
Condition (for finite forcing), Complete sequence of conditions 96
d-prime ideals 225
d-radical ideals 227Ч228
d-radical of an ideal 225Ч227 228Ч231
Deduction Theorem 9
Definability in existentially complete structures, existentially defined subsets in arithmetic 160 162Ч163
Definability in existentially complete structures, of finitely generated division subalgebras 200
Definability in existentially complete structures, of N in existentially complete division algebras 233Ч235
Definability in existentially complete structures, of N in existentially complete models of arithmetic 151
Definability in existentially complete structures, of transcendental elements 203Ч204
Degrees of unsolvability 117Ч131
Degrees of unsolvability of  124Ч125 241 124Ч125 241
Degrees of unsolvability of  121Ч124 125Ч126 184Ч186 244Ч247 121Ч124 125Ч126 184Ч186 244Ч247
Degrees of unsolvability of  121Ч124 125Ч126 184Ч186 244Ч247 121Ч124 125Ч126 184Ч186 244Ч247
Diagram of a structure 7
Division algebra 191Ч252
Division algebra, Existentially complete 195 198Ч222 240
Division algebra, Existentially complete, Embeddings of an 215Ч219
Division algebra, Existentially complete, Extensions of an 215Ч219
Division algebra, Existentially complete, Maximal subfields of an 207Ч214
Division algebra, Existentially complete, Subfields of an 202Ч206
Division algebra, Existentially universal 221 242Ч243
Division algebra, Finitely generated 219Ч222
Division algebra, Finitely generic 219 248Ч249
Division algebra, Finitely homogeneous 200 215Ч216
Division algebra, Infinitely generic 221 243Ч244
Division ring 193
Division ring, Existentially complete 195
Division ring, Existentially complete of characteristic 0 or p 195 (see division algebra also)
Elementary equivalence 9
Elementary extension 9
Elementary substructure 9
Enumeration Theorem (Kleene) 144
| Existential closure (in arithmetic) 139 149 155
Existential completeness of a structure for a theory 17 22Ч28 31 48Ч50 59 69Ч73 77 81 96Ч98 111Ч115 121 129Ч131 132Ч136 141 146Ч154 155Ч189 195 198Ч222 240
Existential completeness of a structure in a class 16 19Ч21 59
Existential completeness of a structure in an extension 16 18
Existential type 29Ч43 65Ч69 72 112Ч115 127Ч128 156Ч157 161Ч163
Existential type of elements in a structure 30 39Ч43 65Ч69 72 156Ч157 161Ч163
Existential type, Defined in a structure 30
Existential type, Defined in a structure, Finite consistency of 33
Existential type, Defined in a structure, Finite satisfiability of 34
Existential type, Maximal existential type 30 39Ч40 41Ч43 112Ч115
Existential type, Realization of 30 155Ч156 161Ч163
Existentially universal structure 31 31Ч43 127Ч129 132Ч136 179Ч181 221 242Ч243
Forcing companions, Finite forcing companion 89Ч93 98Ч103 106Ч110 124Ч125 133 188 241 244 248Ч250
Forcing companions, Infinite forcing companion 70Ч71 119Ч124 125Ч129 131 133 180Ч181 243Ч244 248Ч250
Forcing, Finite forcing in model theory 87Ч110
Forcing, Finite forcing in model theory, by structures 93
Forcing, in set theory 4 55 86
Forcing, Infinite forcing in model theory 55Ч75
Forcing, Weak finite forcing 89
Forcing, Weak infinite forcing 71
Formula,  formula 8 formula 8
Formula, 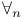 formula 8 formula 8
Formula, Basic sentence 86
Formula, Defined in a structure 7
Formula, Existential formula 8
Formula, Prenex normal form for a 8
Formula, Primitive formula 3
Formula, Universal formula 8
Formula, Universal-existential formula 8
Formulas for arithmetic, 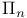 formula 141 formula 141
Formulas for arithmetic, 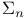 formula 141 formula 141
Formulas for arithmetic, r.e. formula 142
Formulas for arithmetic, recursive formula 142
Generic structure, Finitely generic structure 93Ч100 101 103 108Ч110 111Ч112 132Ч136 188 219 248Ч249
Generic structure, Infinitely generic structure 56Ч64 69Ч73 79 80 82 84 111Ч115 131 132Ч136 179Ч181 221 243Ч244
Groups, Algebraically closed 2 5 16 53 195 222 251Ч252
Groups, Recursively presented 2 5
Henkin theory 119 120
Joint embedding property 52Ч54 70Ч71 101Ч102 125Ч129 133
Language of a structure 7
Matijasevic's Theorem 144 187 248
Model of a theory 8
Model which completes a theory 99Ч100 108Ч110
Model, Generalized elementary classes of models 8
Model, Inductive classes of models 9
Model-companion (of a theory) 3 69Ч72 100Ч103 133 134Ч136
Model-companion (of a theory), nonexistence for division algebras 206
Model-companion (of a theory), of an  -categorical theory 115 -categorical theory 115
Model-complete theory 3 45
Model-completeness for classes of structures 50 53 61Ч64 79Ч80 132
Model-completeness test for a theory 4 46
Model-completion of a theory 2Ч3 45 50Ч51 134Ч136
Model-consistency for classes of structures 50 53 61Ч64 79Ч80 132
Model-consistency for theories 44
Normal expansion of a language 86
Nullstellensatz for commutative fields 15Ч16 223
Nullstellensatz for division algebras 225Ч226
Obstructions to elementary extensions 81
Peano arithmetic 187Ч189
Persistent formula 77
Persistently complete structure 77
Persistently complete structure, 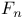 -persistently complete structures 83 -persistently complete structures 83
Persistently complete structure, 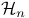 -persistently complete structures 81 -persistently complete structures 81
Persistently complete structure,  -persistently complete structures 77 -persistently complete structures 77
Polynomials, noncommutative 223Ч224
Pregeneric structure 72Ч75 135Ч136 150
Recursive functions, partial or total 142
Reduction Theorems for infinite forcing 66
Reduction Theorems for weak infinite forcing 72
Resultants for infinite forcing 65Ч68 69
Resultants for weak infinite forcing 72 112 114Ч115
Skew polynomial ring 196 210Ч213
Skew power series ring 196 210Ч212
Theory 8
Theory,  8 8
Theory,  141 141
Theory,  9 9
Theory,  9 9
Theory,  9 9
Transcendental elements of a division algebra 199 202Ч204
Ultrapowers, recursively enumerable 156Ч157
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 ,
, 


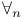 -extension of a structure
-extension of a structure 
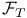

 -equivalence,
-equivalence,  -substructure
-substructure 

 ,
, 
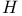 chain
chain  chain
chain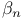 -models
-models 

 formula
formula 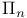 formula
formula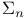 formula
formula  -categorical theory
-categorical theory 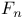 -persistently complete structures
-persistently complete structures 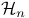 -persistently complete structures
-persistently complete structures  -persistently complete structures
-persistently complete structures



