 -ample III 4 -ample III 4
A-sequence III 4
Albanese variety of X (Alb X) III 2 4.15
Algebraizable formal schemes V 3
Almost base point free dIVisor II 5
Ample cone (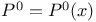 ) I 8 ) I 8
Ample divisor I 2
Ample vector bundle III 1
Arithmetic genus (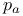 ) III 2 ) III 2
Base locus (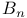 of |nD|) II 5 of |nD|) II 5
Base number or the Picard number ( ) I 8 ) I 8
Base point (of a linear system) I 2
Base point free I 2
Canonical line bundle (K) III 2
Cartier divisor I 1
Chern classes (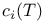 ) III 2 ) III 2
Cofinite module III 5
Cohomological dimension of S (cd(S)) III 3
Complete intersection (strict and set-theoretic) III 5
Complete linear system of dIVisor (|D|) I 2
Complex-analytic space associated to an algebraic variety S (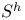 ) III 7 ) III 7
Cone of curves I 8
De Rham cohomology (algebraic) (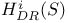 ) III 7 ) III 7
De Rham complex (algebraic) (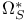 ) III 7 ) III 7
Differentials (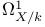 ) III 2 ) III 2
Divisor I 0 1
Divisor class of a divisor I 1
Dualizing differentials III 4
Effective divisor (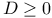 ) I 2 ) I 2
Effective Lefschetz condition (Leff(X, Y)) IV 1
Etale neighborhood V 4.9
Exceptional divisor I 7
Fitting decomposition (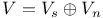 ) III 6 ) III 6
Formal-rational functions V 1
Formal-regular functions V 1
Frobenius morphism  III 6 III 6
Functor G III 6
G1, G2, and G3 V 1
Geometric genus (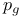 ) III 2 ) III 2
Graded (S, F)-module ((M,f)) III 6
Integers cd(S), p(S), q(S) III 3
Intersection number ((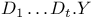 )) I 5 )) I 5
Irregularity of X III 2
Join of two birational varieties (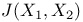 ) II 6 ) II 6
Lefschetz condition (effectIVe) (Leff(X, Y)) IV 1
Lefschetz condition (weak) (Lef(X, Y)) IV 1
Line bundle I 3
Linear system (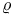 ) I 2 ) I 2
Linearly equivalent divisors (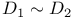 ) I 1 ) I 1
Local equation of a divisor I 1
| Locally a complete intersection III 4
Modification of a scheme III 4
Monoidal transformation III 3.13
Negative vector bundle III 4.14
Nilpotent part ( ) III 6 ) III 6
Normal bundle (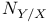 ) III 2 4 ) III 2 4
Numerical polynomial I 5
Numerically effective divisor I 6
Numerically equivalent curves (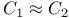 ) I 8 ) I 8
Numerically equivalent divisors (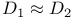 ) I 8 ) I 8
Numerically trivial divisor I 6
P(S) III 3
p-linear endomorphism III 6
Picard group (Pic X) I 1
Poincare residue III 8
Pole sheaf (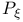 ) IV 3 ) IV 3
Positive line bundle VI 1
Prime divisor I 0
Principle divisor I 1
Projective bundle (scheme) (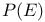 ) III 1 ) III 1
Proper intersection III 4
Pseudo-ample cone I 8
Pseudo-ample divisor I 6
q(S) III 3
q-complete complex space VI 1
q-pseudoconcave complex space VI 1
q-pseudoconvex complex space VI 1
q-pseudoconvex function VI 1
Regular ring V 1
Regular sequence III 4
Restricted inverse limit (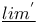 ) III 6 ) III 6
Ruled surface I 10
Second plurigenus (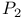 ) III 2 ) III 2
Semi-stable vector bundle I 10
Separates infinitely near points I 2
Separates points I 2
Set-theoretic complete intersection III 5
Stable part (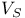 ) III 6 ) III 6
Stable vector bundle I 10
Stein factorization III 4
Stein space VI 1
Support of a divisor (Supp(D)) I 0 1
Tangent bundle (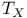 ) III 2 ) III 2
Tautological line bundle (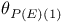 ) III 1 ) III 1
Total transform I 7
Vector bundle III 1
Vector bundle (scheme) (V(E)) III 1
Very ample I 3
Zariski tangent space I 2
Zeros of a section (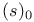 ) I 2 ) I 2
|
 |
|
О проекте
|
|
О проекте



 -ample
-ample 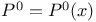 )
) 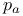 )
) 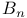 of |nD|)
of |nD|)  )
) 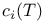 )
) 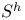 )
) 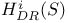 )
) 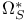 )
) 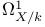 )
)  )
)  )
) 
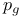 )
) 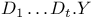 ))
)) 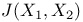 )
) 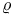 )
)  )
)  )
)  )
)  )
)  )
) 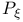 )
) 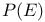 )
) 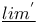 )
) 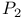 )
)  )
)  )
)  )
)  )
)