|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Epstein R.L. — Degrees of Unsolvability: Structure and Theory |
|
|
 |
| Предметный указатель |
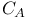 -domination Theorem 154 -domination Theorem 154
 156 156
 160ff 160ff
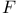 -r.e 197 -r.e 197
 -operator 2 -operator 2
 -jump 126 -jump 126
Agree on the evens 49
Agree on the odds 35
Agree on X 53
Algorithmic class of functions 2
Analysis 116
Analysis,  - 170 - 170
Approximation, recursive 13
Arithmetic 116
Arithmetical degree 14
Arithmetical set 14
atom 191
Automorphism basis 207
Boolean lattice 190
Boolean lattice, generaled by 190
Bottomed 27
Branching 16
Case Defining Lemma 49 68
Chain 190
Characteristic function 2
Church’s thesis 2
Compactness of functionals 8
Compatible strings 5
Compatible strings on the odds 35
Complement 189
Complement, relative 189
Complete r.e. set 12
Computation 3
Computation in time s 4
Computation Lemma 57
Computation Lemma (on the Odds) 39
Computation Lemma (recursive case) 18
Correspondence Corollary 173
Cover 188
Cover, minimal 34
De Morgan’s Identities 189
Definable a is, in arithmetic 184
Definable in 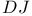 116 116
Definable in 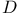 116 116
Definable in Analysis 116 130
Definable with parameters in 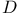 132 132
Defined at stage s 11
Defining pair for level of a tree 37
Degree of unsolvability 9
Diagonalization lemma 56 (see also “Posner’s Lemma”)
Diagonalization Lemma (recursive case) 54
Diagonalization Lemma (weak form) 55
diamond 48
Distributive lattice 187
Distributive lattice of specified degree 106ff
Dominates, function 154
Double Limit Lemma 91
Exact pair 118
Extension on a tree 16
f-r.e 153 197 210
Finite injury 147
Forces the jump 139 140
Forces the jump, relative to a tree 140
Full approximation construction 145 162
Full subtree above 17
Full tree 17
Fully uniform tree 37
Functional, partial recursive 6
Functional, partial recursive, compactness of 8
Functional, partial recursive, consistency condition 6
Functional, partial recursive, standard enumeration of 7
High degree 157ff
High set 159
Homogeneity conjecture 31 234
Homogeneity conjecture, strong 32 106 202 229
Hugill’s conditions 227
Ideal of degrees 117
Ideal of degrees, Characterization of 117
Identity tree 15
Incompatible strings 5
Index for a p.r. function 4
Index for a p.r. functional 8
Infinite injury 91ff
Initial segment of degrees 27
Interval in a lattice 189
Introreducible set 141
Join 187
Join-irreducible 190
Jump of A 10
Jump, 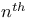 - 10 - 10
Jump,  - 126 - 126
Jump, forces the 139 140
Jump, operator 10
Jumps and Chains Theorem 103
Kleene T-predicate 3
Lattice 187
Lattice, bottomed 27
Lattice, distributive 187
Lattice, homomorphism 187
Lattice, sub- 187
| Lattice, topped 74
Lattice, upper-semi- 187
Least search operator ( ) 2 ) 2
Length of a string 5
Lies on a tree 16
Lies on a tree, above 16
Lies on a tree, below 16
Limit Lemma 13
Limit of functions 11
Meet 187
Meet-irreducible 190
Miller & Martin’s Lemma 154
Minimal cover 34
Minimal degree 20
n-minimal over 133
n-r.e. degree 153 195ff 210
n-r.e. set 152
Node of a tree 16
Node of a tree, S-O 42
Normal Form Theorem 3
Odds, the, agree on 35
Odds, the, compatible on 35
Odds, the, part of 34
Odds, the, Special on 35
Order Reversing Correspondence 120
Ordering of strings 6
O’-oracle construction 162
Pairing function 3
Partial recursive (p.r.) function 3
Partial recursive (p.r.) functional 6
Partial recursive (p.r.) functions in A 3
Partial recursive (p.r.) tree 17
Partition Representation Theorem 191ff
Passes through, a string 16
Perfect closed set 230
Permitting argument 145ff 163
Posner’s Lemma 19 201
Power set of X 188
Presentable, a- 88
Primitive recursive functions 3
Priority argument 89 142ff 163
Projection function 2
Q (sub-theory of arithmetic) 177
Quantifier Characterization of Sets Below 0/ 13
RECURSIVE see “Partial recursive”
Recursive approximation 13
recursive functions 13
Recursively enumerable (r.e.) 12 212 “f-r.e.” “ “n-r.e.”)
Recursively enumerable (r.e.) complete r.e. set 12
Recursively enumerable (r.e.) in A (in a) 12
Recursively isomorphic sets 136
Recursively isomorphic sets, theories 136
Relativize 31 96
Representable, a function,in arithmetic,is 177 178
S-m-n theorem 4
Simultaneously r.e. (s.r.e.) 172
Special on the Odds (S-O) 35
Special on the Odds (S-O), defining pair with respect to tree T 38
Special on the Odds (S-O), node 42
Special on the Odds (S-O), tree 38
Special, 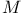 - 67 (see also “S-E” “S-X”) - 67 (see also “S-E” “S-X”)
Spector’s Theorem 23
Splitting, e- 17
Splitting, e-, at stages 17
Splitting, e-, tree 18
Splitting, tree 18
String(s), compatible 5
String(s), empty 5
String(s), extends 16
String(s), incompatible 5
String(s), length of 5
String(s), lies above, below 16
String(s), ordering of 6
Sublattice 187
Subtree 17
Successor function 2
T-predicate 3
Titgemeyer’s representation 226
Topped 74
Tower,  - 133 - 133
TREE 15
Tree, 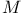 -special 67 -special 67
Tree, branching of 16
Tree, defining pair for level of 37
Tree, degree of 15
Tree, full subtree of 17
Tree, full- 17
Tree, fully uniform 37
Tree, identity 15
Tree, node of 16
Tree, of trees 96 220
Tree, partial recursive 17
Tree, S-O 38
Tree, S-X 54
Tree, splitting tree for e 18
Tree, subtree 17
Tree, uniform 37
Turing degree 9
Turing reducibility 9
Uniform tree 37
Upper-semi-lattice 187
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



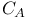 -domination Theorem
-domination Theorem 

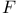 -r.e
-r.e  -operator
-operator  -jump
-jump  -
- 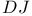
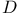
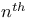 -
- 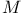 -
-