|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Wojtaszczyk P. — A Mathematical Introduction to Wavelets |
|
|
 |
| Предметный указатель |
Atom, special 214
Bernstein's inequality 225
Besov norm 220
Besov spaces 220
Besov spaces, inhomogenous 230
Biorthogonal functionals 20
Biorthogonal system 173
Calderon — Zygmund decomposition 147
Cohen's condition 100 124
cube 141
Cube, dyadic 146
Dilation 107
Dilation, dyadic 18
Distribution of function 141
Dyadic intervals 1
Equivalent bases 200
Exponential decay 8 58 61
Frame 20
Frame, light 20 100
Function of bounded p-mean oscillation 149
Function,  -periodic 246 -periodic 246
Function, r-regular 116
Hardy — Littlewood maximal function 142 146
Hardy's inequality 167
Hilbert transform 166
Hoelder's condition 15 218 220
Hoermander condition 167
Jackson's inequality 223
John — Nierenberg theorem 154
Khintchine's inequality 176
Lebesgue Differentiation Theorem 144
Marcinkiewicz interpolation theorem 145
Markov's inequality 141
Matrix, banded 64
Matrix, Toeplitz 65
Multipliers 164
Multiresolution analysis 17
Multiresolution analysis, Meyer 49
Multiresolution analysis, on 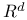 108 108
Multiresolution analysis, r-regular 116
Operator of weak type  160 160
| Operator of weak type (1,1) 145
Operator of weak type (p,p) 160
Operator, dilation 18 140
Operator, sublinear 145
Operator, translation 18 140 167
Order 168
Orlicz theorem 179
Orthogonality of translates 23 111 113
p-modulus of continuity 216
q-atom 150
Rademacher functions 175
Riesz basis 111 174
Riesz lemma 83
Riesz sequence 20 28 110 173
Scaling equation 27
Scaling function 18 26 31 32 108
Schwartz class 49
Series, absolutely convergent 173
Series, unconditionally convergent 168
Set of digits 109
Special atoms space 222
SPLINE 52
Spline, B-spline 52
Stone — Weierstrass theorem 215
Support of compactly supported wavelet 81
Tile 122
Unconditional basis 174
Unit vector basis 241
Vanishing moments 47
Wavelet 17
Wavelet basis 17
Wavelet of exponential decay 61
Wavelet set 107
Wavelet, associated with multiresolution analysis 33
Wavelet, compactly supported 75 105 201
Wavelet, general form 37
Wavelet, Haar 1 103
Wavelet, Meyer's 50 207
Wavelet, multidimensional 107
Wavelet, not associated with multiresolution analysis 66
Wavelet, spline 56
Wavelet, Stroemberg 6
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -periodic
-periodic