|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Weil A. — Foundations of Algebraic Geometry |
|
|
 |
| Предметный указатель |
Abstract field I 1 1
Abstract variety VII 1 167
Algebraic closure I 1 1
Algebraic closure in I 1 1
Algebraic over (a field), bunch of varieties IV 4 85
Algebraic over (a field), normally IV 4 86
Algebraic over (a field), separably I 4 8
Algebraic over (a field), set of generalized quantities II 1 28
Algebraic over (a field), set of quantities 1 2 2
Algebraic over (a field), variety IV 2 76 (a.c.) 2 177
Algebraic projection (of cycles) VII 6 208
Algebraically closed in (a field) I 1 1
Ambient Space IV 1 69
Ambient Variety VII 2 174
Attached to, linear variety, a variety IV 6 98
Attached to, point-set, a bunch of varieties IV 4 84
Attached to, point-set, a variety IV 1 69 (a.c.) 2 178
Birational correspondence IV 7 109 (a.c.) 4 188
Birationally equivalent IV 7 109
Biregular IV 7 110 (a.c.) 4 189
Bunch of varieties IV 4 84 (a.c.) 2 178
Bunch of varieties algebraic (normally algebraic) over a field IV 4 85—86
Bunch of varieties, empty IV 4 84
Bunch of varieties, point of (in) a IV 4 84
Bunch of varieties, point-set attached to a IV 4 84
Coefficient (of a Variety in a cycle) VII 6 197
Coherent (birational correspondences) VII 1 166
Compatible (specialization, with) II 2 30
complete VII 1 168
Complete over (a Point, a Variety) VII 4 185—186
Complete set of conjugates I 4 9
Complete set of intersections V 1 119
Component of a bunch (of an intersection) IV 4 85 (a.c.) 2 178
Component of a cycle VII 6 197
Component, proper, of an intersection V 1 117 VI 1 146 (a.c.) 5 189
Cone App. I 263
Conjugate of a bunch of varieties IV 4 86
Conjugate of a set of quantities 1 4 9
Conjugate of a variety IV 2 76 (a.c.) 2 177
Conjugate, complete set of I 4 9
Constant VIII 1 216
Contain (to), contained in, (bunches of varieties) IV 4 84
Contain (to), contained in, (varieties) IV 1 69 (a.c.) 1 170
Contain (to), contained in, cycle contained in a Variety VII 6 212
Coordinate of a point IV 1 68
Coordinate of a Point of D, VIII 1 215—216
Correspondence (birational) IV 7 109 (a.c.) 4 188
Corresponding, generic points (by a birational correspondence) IV 7 110
Corresponding, generic points (by a set of coherent birational correspondences) VII 1 166
Corresponding, regularly (points, varieties, by a birational correspondence) IV 7 110 (a.c.) 4 189
CYCLE VII 6 197
Cycle, component of VII 6 197
Cycle, degree of VII 6 198—199
Cycle, expression (reduced expression) for a cycle VII 6 197
Cycle, generic Point of a prime rational, over a field VII 6 200
Cycle, positive VII 6 198
Cycle, rational, prime rational (over a field) VII 6 198
Cycle, specialization of (of dimension 0) VII 6 205
def (as symbol) IV 1 72
Defined, bunch of varieties, over (a field) IV 4 85
Defined, function, along (a Variety) VIII 1 218
Defined, function, over (a field) by (a relation) VIII 1 216
Defined, variety, by (an ideal, a set of equations) IV 1 70
Defined, variety, by (representatives, frontiers and birational correspondences) VII 1 167
Defined, variety, over (a field) IV 1 68 (a.c.) 1 167
Defining, (ideal, set of equations), (a variety) IV 1 70
Definition cf. “Field of definition”
deg (as symbol) VII 6 198 and 266
Degree (of a cycle in a projective space) App. I 266
Degree (of a cycle of dimension 0) VII 6 198
Degree (of an algebraic extension) I 2 2
Degree, separable (inseparable) factor of the, (of an algebraic extension) I 4 9
Derivation I 5 11
Determined, ideal, by (a set of quantities) over (a field) I 3 6
Diagonal VI 1 143 (a.c.) 4 189
dim (as a symbol) I 2 2; 1 27; 1 72 (a.c.) 2 173
Dimension of (a cycle) VII 6 197
Dimension of (a set of generalized quantities) over (a field) II 1 27
Dimension of (a variety) IV 1 72 (a.c.) 2 173
Dimension of (an extension, a set of quantities) over (a field) I 2 2
Disjoint, linearly I 2 4
Divisor VII 6 198
Divisor of (a function) VIII 2 224
Empty (bunch of varieties) IV 4 84
Equation, generic set of linear IV 5 96
Equation, irreducible (for a set of quantities over a field) I 3 8
Equation, minimal set of linear (for a linear variety) IV 5 93
Equation, set of (for a variety, or defining a variety) IV 1 70
Equivalent (birationally) IV 7 109
Expression, reduced (for a bunch of varieties) IV 4 85
Expression, reduced, (for a cycle) VII 6 197
Extend (to) a specialization II 2 30
Extension (of a field) I 1 2
Extension (of a field), algebraic I 2 2
Extension (of a field), degree of an (algebraic) cf. “Degree”
Extension (of a field), dimension of an I 2 2
Extension (of a field), purely inseparable I 4 8
Extension (of a field), purely transcendental I 2 4
Extension (of a field), regular I 7 18
Extension (of a field), separable (separably algebraic) I 4 8
Extension (of a field), separably generated I 5 14
Extension (of a specialization) II 2 30
Factor (of a product of varieties) IV 3 79 (a.c.) 3 183
Factor (of a product of varieties), separable (inseparable), of the degree (of an algebraic extension) I 4 9
Field I 1 1
Field generated by (a set of quantities) over (a field) I 1 2
Field of definition, (for a function) VIII 1 216
Field of definition, (for a variety) IV 1 68 (a.c.) 1 167
Field of definition, smallest (for a variety) IV 1 72
Field, abstract I 1 1
Field, independent, free I 2 3
Field, prime I 1 1
Finite over (a specialization) II 5 41
Finite, (quantity), at (a point) App. II 268
Finite, (set of generalized quantities) II I 27
Finite, (variety), over (a point) IV 7 106
Free (field, extension) I 2 3
Frontier VII 1 166
Full set of representatives VII 1 168
Function VIII 1 216
Function defined along (a Variety), induced on (a Variety) by (a function) VIII 1 218
Function defined over (a field) by (a relation) VIII 1 216
Function, constant, constant generalized VIII 1 216
Function, divisor of a VIII 2 224
Function, field of definition for a VIII 1 216
Function, generalized VIII 1 217
Function, graph of a VIII 1 218
Generalized function VIII 1 217
Generalized, quantity II 1 26
Generated, (extension), by (a set of quanlities) over (a field) I 1 2
Generated, separably 1 5 14
Generic Point of (a prime rational cycle) over (a field) VII 6 200
Generic point of (a variety) over (a field) IV 1 68 (a.c.) 2 173
Generic set of linear equations over (a field) IV 5 96
Generic, (specialization) II 1 27
Generic, corresponding, points by (a birational correspondence) IV 7 110
Generic, corresponding, points by (a set of coherent birational correspondences) VII 1 166
Graph (of a function) VIII 1 218
Homogeneous ideal App. I 264
Homogeneous, set of, coordinates App. I 263
Homogeneous, set of, equations, App I 265
i (as a symbol) VI 1 148 (a.c.) 5 189
Ideal defining (a variety over a field) IV 1 70
Ideal, determined by (a set of quantities) over (a field) I 3 6
Independent, (extensions, sets of quantities) I 2 3
Independent, (variables) I 2 4
Induce (to), induced by (function) VIII 1 218
Infinite II 1 27
Inseparability, (for a variety) V 1 123 (a.c.) 2 177
Inseparability, order of (for an extension) I 8 22
| Inseparable I 4 8
Inseparable, factor of the degree I 4 9
Inseparable, purely, over (a field) I 4 8
Integral over (a ring) III 3 52
Integrally closed App. II 268
Intersect, to, properly VII 6 201
Intersection, (of varieties, of bunches of varieties) IV 4 88—89 (a.c.) 2 178
Intersection, complete set of V 1 119
Intersection, point of V 1 117
Intersection, proper component of an V 1 117 VI 1 146 (a.c.) 5 189
Intersection-multiplicity V 1 121 V 2 130 VI 1 148 (a.c.) 5 189
Intersection-product VII 6 202
Irreducible equation (for a set of quantities over a field) I 3 8
Isolated specialization II 3 32
j (as a symbol) V 1 121 V 2 130
Lie, to, properly over (a Point, a Variety) VII 4 186
Linear equations, generic set of, over (a field) IV 5 96
Linear equations, minimal set of (for a linear variety) IV 5 93
Linear equations, set of IV 5 90
Linear forms, unlformizing set of IV 6 100—102
Linear variety IV 5 90
Linear variety attached to (a variety) at (a point) IV 6 98
Linear variety, parallel IV 5 95
Linear variety, tangent, to (a variety) at (a point) IV 6 99
Linear variety, transversal IV 5 95
Linearly disjoint I 2 4
Locus of (a point) over (a field) IV 1 68 (a.c.) 2 174
Maximal multiple subvarlety IV 6 99 (a.c.) 2 179
Maximal variety (in a bunch) IV 4 85
Maximal variety, belonging to (a point-set) IV 4 84 (a.c.) 2 178
Minimal set of linear equations IV 5 93
Multiple subvarlety IV 6 99. 2 179
Multiple, maximal, subvariety IV 6 99 (a.c.) 2 179
Multiple, point IV 6 99 (a.c.) 2 179
Multiplicity (of a component of an intersection) cf. “Intersection-multiplicity”
Multiplicity (of a specialization) III 4 62
normal App. II 277
Normal, relatively App. II 277
Normalization App. II 273
Normally algebraic IV 4 86
Operations (on cycles), algebraic projection VII 6 208
Operations (on cycles), intersection-product VII 6 202
Operations (on cycles), operation X VII 6 203
Order of inseparability cf. “Inseparability”
Over (a field) I 1 1 etc
Over (a specialization, with reference to a field) II 2 30
Over, finite cf. “Finite”
Over, proper specialization (a specialization) cf. “Proper”
Over, to lie properly cf. “Properly”
p (as symbol for the characteristic) I 1 1
p (as symbol for the characteristic), 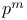 1 4 8 1 4 8
Parallel (linear varieties) IV 5 95
Partial product IV 3 79
Point IV 1 68 (a.c.) 2 173
Point of (a bunch of varieties), in (a bunch of varieties) IV 4 84—85
Point of (a variety), on (a variety) ill (a variety) IV 1 69 (a.c.) 2 173
Point, generic cf. “Generic”
Point, locus of a cf. “Locus”
Point, multiple IV 6 99 (a.c.) 2 179
Point, regularly corresponding cf. “Regularly”
Point, set of IV 1 68
Point, simple IV 6 99 (a.c.) 2 179
Point-set IV 1 68 (a.c.) 2 178
Positive cycle VII 6 198
pr (as a symbol) VII 6 208
Prime rational cycle over (a field) VII 6 199
Prime, field I 1 1
Product, product-variety IV 3 79 (a.c.) 3 181
Product, product-variety, factors of a IV 3 79 (a.c.) 3 183
Product, product-variety, partial (of a product) IV 3 79
Projection IV 3 80—81 (a.c.) VII 3 184
Projection from (a variety) to (a variety) IV 7 105 (a.c.) 4 185
Projection, algebraic (of a cycle) VII 6 208
Projection, regular, along (a variety) IV 7 108 (a.c.) 4 187
Projection, regular, at (a point) IV 7 108 (a.c.) 4 187
Projective space App. I 262
Projective straight line VIII 1 215
Proper component (of an intersection) V 1 117 VI 1 146 (a.c.) 5 189
Proper, specialization III 4 62
Properly, to intersect VII 6 201
Properly, to lie, over (a Point, a Variety) VII 4 186
Pseudopoint IV 1 68 (a.c.) 2 174
Purely transcendental (extension) I 2 4
Purely, inseparable I 4 8
quantities I 1 1
Quantities, generalized, set of generalized II 1 26
Quantities, set of I 1 1
Rational (cycle) over (a field) VII 6 198
Rational (cycle) over (a field), prime, (cycle) over (a field) VII 6 199
Reciprocation II 1 26
Reduced expression (for a bunch of varieties) IV 4 85
Reduced expression (for a cycle) VII 6 197
Reduced, (variety) to (a point) IV 1 69 (a.c.) 2 173
Reference, with, to (a field) I 1 1 etc
Regular over (a field), extension of (a field) I 7 18
Regular projection IV 7 107 (a.c.) 4 187
Regular projection along (a variety) IV 7 108 (a.c.) 4 187
Regular projection at (a point) IV 7 108 (a.c.) 4 187
Regularly corresponding, (points) IV 7 110 (a.c.) 4 189
Regularly corresponding, (varieties) IV 7 110 (a.c.) 4 189
Representation VII 2 173 VII 3 184
Representative (of a Point) VII 2 173
Representative (of a specialization of a set of corresponding generic points of the representatives of a Variety) VII 1 168
Representative (of a Subvariety, in a representative of the ambient Variety) VII 1 171
Representative (of a Variety) VII 1 167
Representative, full set of, attached to (a Variety) VII 1 168
Represented (simultaneously) VII 2 172 VII 3 184
Separable I 4 8
Separable factor of the degree 1 4 9
Separably generaled (extension) I 5 14
Separably, algebraic I 4 8
Set of equations, of linear equations cf. “Equations”
Set of generalized quantities II 1 26
Set of points, of points and pseudopoints IV 1 68
Set of points, of points and pseudopoints (for “point-set”) cf. “Point-set”
Set of quantities I 1 1
Set, complete, of conjugates I 4 9
Set, complete, of intersections V 1 119
Set, full, of representatives cf. “Representatives”
Set, uniforniizmg, of linear forms cf. “Uniformizing”
Simple, (point) IV 6 99 (a.c.) 2 179
Simple, (subvariety) IV 6 99 (a.c.) 2 179
Simultaneously represented VII 2 172 VII 3 184
Smallest field of definition for (a variety) IV 1 72
Space, n-space IV 1 69
Space, n-space, ambient IV 1 69
Space, n-space, product-space IV 3 80
Specialization of (a cycle of dimension 0) VII 6 205
Specialization of (a Point) over (a field), generic, of (a Point) over (a field) VII 2 175—176
Specialization of (a set of generalized quantities) over (a specialization) with reference to (a field) II 2 30
Specialization of a set of linear equations IV 5 95
Specialization, (of a set of generalizedquantities, over a field) II 1 27
Specialization, extension of a, to extend a II 2 30
Specialization, finite (of a set of quantities) II 1 26
Specialization, finite (set of quantities) over a II 5 41
Specialization, generic II 1 27
Specialization, isolated II 3 32
Specialization, multiplicity of a III 4 62
Specialization, proper III 4 62
Specialization-ring II 4 36
Specialization-ring of a point, of a subvariety IV 2 77 (a.c.) 2 176
Subvariety IV 1 09 (a.c.) 1 170
Subvariety, simple, multiple, maximal multiple IV 6 99 (a.c.) 2 179
Subvariety, specialization-ring of a IV 2 77 (a.c.) 2 176
Tangent linear variety IV 6 99
Transversal, (linear varieties) IV 5 95
Transversal, (varieties) VI 2 152 (a.c.) 5 190
Uniformizing set of linear forms, along (a subvariety) IV 6 102
Uniformizing set of linear forms, at (apoint) IV 6 100
Union (of varieties, of bunches of varieties) IV 4 84 (a.c.) 2 178
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте