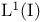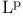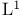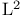Weir A.J. — Lebesgue Integration and Measure :: Электронная библиотека попечительского совета мехмата МГУ

Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск Форум

Авторизация

Поиск по указателям

Weir A.J. — Lebesgue Integration and Measure

Обсудите книгу на научном форуме

Нашли опечатку?
Выделите ее мышкой и нажмите Ctrl+Enter

Название: Lebesgue Integration and Measure

Автор: Weir A.J.

Аннотация:

Lebesgue integration is a technique of great power and elegance which can be applied in situations where other methods of integration fail. It is now one of the standard tools of modern mathematics, and forms part of many undergraduate courses in pure mathematics.

Dr Weir's book is aimed at the student who is meeting the Lebesgue integral for the first time. Defining the integral in terms of step functions provides an immediate link to elementary integration theory as taught in calculus courses. The more abstract concept of Lebesgue measure, which generalises the primitive notions of length, area and volume, is deduced later.

The explanations are simple and detailed with particular stress on motivation. Over 250 exercises accompany the text and are grouped at the ends of the sections to which they relate: notes on the solutions are given.

Язык:

Рубрика: Математика/

Статус предметного указателя: Готов указатель с номерами страниц

ed2k: ed2k stats

Год издания: 1973

Количество страниц: 293

Добавлена в каталог: 28.07.2008

Операции: Положить на полку | Скопировать ссылку для форума | Скопировать ID

Предметный указатель

$\mathrm{L}^\mathrm{1}$       37—43 47—50 78—81
$\mathrm{L}^\mathrm{1}(\mathrm{A})$       126
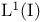$\mathrm{L}^\mathrm{1}(\mathrm{I})$       40 79
$\mathrm{L}^\mathrm{inc}$       33—36 41 46 78
$\mathrm{L}^\mathrm{inc}(\mathrm{A})$       126
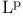$\mathrm{L}^\mathrm{p}$       162—222
$\mathscr{L}^\mathrm{p}$       165—166
Absolutely convergent series      5
Affine mapping      139—144
Almost everywhere      32 77
Almost everywhere, convergence      168
angle      174
Archimedes, Axiom of, 3n      14 164
Area      71 82 87
Baire classes      122
Ball, closed      82
Ball, open      82 224
Banach space      221
Bessel's equation      198
Bessel's inequality      198
Bolzano — Weierstrass theorem      239
Bonnet's Mean Value Theorem      134 210
Borel seta      145
Boundary      227
Bounded convergence theorem      110 112
Bounded set      233
Bounded variation      65 209
Brouwer's theorem      158
Cantor      16 17
Cantor, ternary set      20 69 145
Cauchy General Principle of Convergence      116 163 169
Cauchy sequence      164
Cesaro      211 218
Characteristic function      23 72
Clarkson's inequalities      181
Closed ball      82
Closed disk      82
Closed set      135 227
Closure      193 227
Closure of an interval      71
Compact set      135 234—236
Completeness of 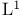$\mathrm{L}^1$       42
Completeness of 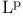$\mathrm{L}^\mathrm{p}$       170
Completeness of a metric space      164
Completeness of a set in 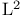$\mathrm{L}^2$       196
Completeness of R      2—13 162—164
complex numbers      13
Connected set      229—233
Continuous function      46—50 79—81 228—238
Continuously differentiable function      156
Convergence of a sequence      2—10
Convergence of a series      5
Convergence, almost everywhere      168—171
Convergence, in mean (strong)      168—171 207
Convergence, pointwise      168—171 202—214
Convex set      176
Countable set      15
Cross-section      85 87
cube      71
Darboux's theorem      52
Decimal expansion      5—7 10 17
Decreasing function      48
Decreasing sequence      2
Dedekind's Theorem      14
Dense      15 196
Density function      146—161 185—186
Derivative      55—69
Derivative measure      152—154
Derivative, directional      155
Derivative, linear      156—159
Derivative, partial      155
Determinant      144
Differentiation under the integral sign      118
DIMENSION      192
Dirichlet kernels      206—213 216—217
Disk, closed      82
Disk, open      82 89
Distance      1 70 155 223
Dominated Convergence Theorem      106 109 113
du Bois-Reymond      214
Dual spaces      166 184 187
Eigenvalue, maximum      240
Elementary figure      75
Erlanger Programm      134
Euclidean space      70—92 124 219
Exchange Lemma      193
Exterior      227
Fatou's lemma      110 116
Fejer      211
Fejer kernels      212—214
Fejer theorem      213 214
Finite dimensional subspace      191
Fourier series      188 194—199 202—219
Fubini's theorem      83 90 123 142
Function      22
Function absolutely continuous      67
Function of bounded variation      65 209
Function, continuous      46—50 79—81 228—238
Function, continuously differentiable      156
Function, generalised step      128
Function, increasing, decreasing, monotone      48
Function, measurable      120—124 128—133
Function, simple      128 130
Function, step      25—30 72—76
Fundamental theorem of the calculus      56 67 112
Gamma function      111
Geometry      134
Geometry, of 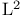$\mathrm{L}^2$       172—181
Gibbs' constant      218
Gibbs' phenomenon      207 218
Gram — Schmidt Theorem      191
Hausdorff space      238
Heine — Borel theorem      34 233
Heisenberg matrix theory      200
Hermite functions      201
Hilbert space      221—222
Hoelder's inequality      167
Homeomorphism      144 238
Hyperplane      71
Increasing function      48
Increasing sequence      2
Infimum      9
Inner product      172
Integers      1
Integrable function      37 79

Integrable set      125
Integral, definite      44—50
Integral, indefinite      54—62
Integral, Lebesgue      37—43 79—91
Integration by parts      58 103
Integration by substitution      59 104
Interior      227
Intermediate Value Theorem      231
interval      1 2 70 71
Interval length      2
Interval measure      71
Inverse mapping theorem      159
Isometry      137—144
Jacobian formula      158
Jacobian matrix      155
Jordan's Theorem      209
Klein, Felix      134
Laguerre polynomials      200
Lebesgue      ix et sqq. 202
Lebesgue integral on $\mathrm{R}^\mathrm{k}$       70—92
Lebesgue integral on R      22—69
Lebesgue measure      124 et sqq.
Legendre polynomials      200 202
Length      2 24 28 87
Levi, Beppo      93 107
Limit point      226
Linear dependence, independence      192 194
Linear functionals      182
Linear mapping      138
Linear operator      72
Linear space      22 72 165 199 220
Linear subspace      176 220
Lipschitz condition      69
Localization principle      206
Lower bound      3 9
Matrix      139
Matrix, unit, invertible, elementary, diagonal      140
Mean value theorem      237
Mean Value Theorem for Integrals      41
Mean, arithmetic, geometric      62
Measurable function      120—124
Measurable set      124
Measure      75 87 124—146
Measure, derivative      152
Measure, of a bounded interval      71
Metric      223
Metric space      163 220 223
Metric, complete      164
Metric, discrete      224
Minkowski's inequality      167 172
Monotone Convergence Theorem      93 96 103 106
Monotone function      48
Monotone sequence      2
Neighbourhood      239
Nested intervals      14
Non-measurable set      131
Norm      70 154 165 199 220
Null set      18 77
Open ball      82 224
Open set      135 225 237
Open, relatively      230
Ordered field      12
Ordinate set      88 133
Origin      1
Orthogonal      174
Orthogonal complement      180
Orthogonal projection      180
Orthonormal set      191—201
Parallelogram      175
Parseval's equation      199—200
Pointwise convergence      168—171 202—214
Polar transformation      146 159
Polar transformation, cylindrical      159
Polar transformation, spherical      160
Positive      1
Projection      179
Pythagoras' theorem      6 7 174
Radon — Nikodym theorem      152 185
Rational numbers      1
Real line      1
Relatively open set      230
Riemann integral      47 51—54 83
Riemann integral, improper      106
Riemann — Lebesgue lemma      115 204
Riesz — Fischer theorem      199
Riesz's Toolroom for 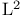$\mathrm{L}^2$       183
Rolle's theorem      236
Scalar product      137 199 221
Scalar product (inner product)      172
Schroedinger      200
Schwarz' inequality      137 173
Segment      174
SEQUENCE      2
Sequence, convergence almost everywhere      168—171
Sequence, convergence in mean      168—171 207
Sequence, increasing, decreasing, monotone      2
Sequence, pointwise convergence      168—171 202—114
Sequence, upper, lower      107
Series      4
Series, absolute convergence      5
Series, convergence      5
Series, convergence in 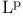$\mathrm{L}^\mathrm{p}$       169
Sets, union, intersection, difference, symmetric difference of      23
Simple function      128—130
Step function      25—30 72—76
Step function, generalised      128
Strong convergence      168—171 207
Summable (O,1)      211
Supremum      9 12
Symmetric difference      23
Tonelli's theorem      123
Topological mapping      144 238
topology      223—240
Topology, general      226 237
Triangle inequality      138 165 173 223
Trigonometric polynomial      190
Uniform continuity, convergence      218
Upper bound      3 9 12
Variation, bounded      65 68
Variation, positive, negative      68
Variation, total      68
Vector space      220
Volume      71 73 83 87
Weierstrass' approximation theorem      218
Well-ordering of positive integers      8
Zorn's lemma      221

О проекте