|
Электронная библиотека Попечительского совета механико-математического факультета Московского государственного университета |
| Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск |
© Электронная библиотека попечительского совета мехмата МГУ, 2004-2026 |
|
О проекте |
|
О проекте
|



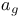
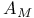
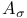
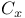
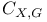
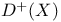
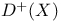
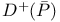
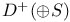
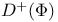
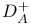
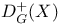
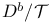
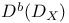
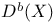
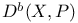
![$D^b([G\X].)$](/math_tex/969704dbe281d5a66a94410221d3c2ac82.gif)
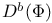
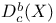
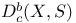
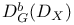
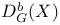
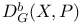
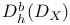
![$D^b_{eq}([G\X].)$](/math_tex/9b94f364fc396c8b417f4bcfaee99abe82.gif)
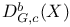
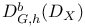
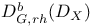
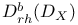
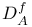
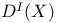
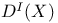
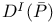
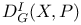
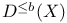 ,
, 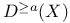
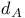
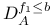 ,
, 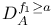
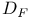
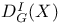
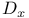
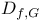
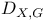
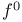
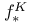
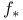 ,
, 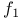 ,
, 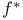 ,
, 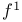
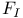
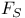
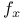
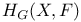
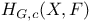


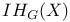
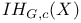
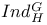
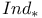


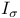

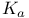


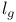
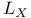

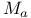










![$Sh_{eq}([G\X].)$](/math_tex/be252a030a1a8468eb6648e0c719284682.gif)


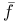
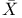

 -acyclic map
-acyclic map 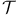
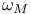
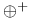

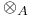

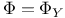
 -map
-map 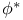
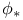
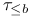 ,
, 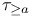
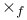
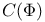 of the fibered
of the fibered