|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Kahane J.-P. — Fourier Series and Wavelets, Vol. 3 |
|
|
 |
| Предметный указатель |
"a trous" algorithm 8.1
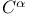 (Hoelder space) 1.5 (Hoelder space) 1.5
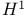 (Hardy space) 6.3 (Hardy space) 6.3
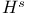 (Sobolev space) 1.5 (Sobolev space) 1.5
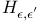 1.1 2.2 1.1 2.2
 6.2 6.2
 -transform 0.3 2.6 -transform 0.3 2.6
2-microlocalization 0.3 see
Adelson 0.4 0.5 8.2
Admissibility condition 0.2 1.4 7.1
Affine group 0.2 7.1
Almost orthogonal family 1.2 2.2 2.4
Almost wavelets 5.2
Analytic wavelet transform 1.4 8.1
Approximation order 5.2
Arneodo 0.2
Aslaksen 0.2
Asymptotic signals 10.4
Atoms, atomic decomposition 0.3 6.3
Atoms, time-frequency atoms 9.4
Auscher 3.2 3.4 7.2
B-spline 5.3
Baastians 1.3
Balian 1.3
Balian — Low uncertainty theorem 0.3 1.3
Barnwell 0.4
Bases see "Wavelet bases"
Battle 0.3 1.3 5.2 5.3 7.1
Battle — Lemarie wavelet 0.3 5.2 5.3
BCR algorithm 0.3 8.5
Berkolaiko 5.2
Berkolaiko — Novikov basis 5.2
Besov spaces 0.3 2.6 5.2 6.5 7.3 8.6
Besov spaces, homogeneous 6.5
Best basis 9.2 9.3
Beylkin 0.3 8.4 8.5
Bi-orthogonal wavelets, bi-orthogonal multiresolution analyses 0.5 3.0 3.2 3.3 5.4 6.1
BMO, 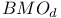 , bmo 6.3 , bmo 6.3
Bony 0.3 2.6 6.6 10.1
Bourdaud 6.5
Bourgain 1.3
Box-splines 7.1
Bump element 6.5
Burt 0.4 0.5 8.2
Butterworth scaling filter 5.2
Calderon 0.3 2.6 6.1
Calderon identity 0.3 2.6
Calderon — Zygmund operators 0.3 0.5 6.1 6.4 6.5 8.5 10.1 10.3
Calderon — Zygmund splitting 6.2
Cascade algorithm 5.2 8.4
Chirps 0.3 10.4
Chui 2.1 3.4 5.3
Cohen 4.2 4.3 5.1 5.2 5.4 7.3 8.3
Cohen criterion 4.2 4.4 5.1
Coherent states 0.2
Coiflets 5.2 8.4
Coifman 0.3 0.4 5.2 6.1 6.3 8.4 8.5 9.2 9.3 10.2 10.3
Compression 0.3 0.4 8.6 9.2
Continuous wavelet transform 0.2 8.1 see
Conze 5.1
Correlation function 3.1
Correlation matrix 3.1
Daubechies 0.2 0.3 0.5 1.3 2.1 2.6 4.3 5.1 5.2 5.4 7.3 8.0 8.1 8.3 8.4
Daubechies orthonormal wavelets 0.5 5.2
David 0.5 3.3 10.1 10.3
David — Journe theorem 0.5 10.3
De-noising 8.6
Derivative of a scaling functions 4.2 8.4
Deslauriers 5.1
Dilation matrix 7.1
Discrete wavelet transform 0.1 0.2 2.1 2.5 7.1
Div-curl theorem 10.2
Divergence-free vector fields 7.1
Dobyinsky 10.1 10.2
Donoho 0.3 8.6
Dual frame 1.2 2.5
Dubuc 5.1
Duffin 0.2
Durand 8.4
Dyadic 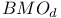 , dyadic Hardy space , dyadic Hardy space 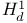 6.3 6.3
Dyadic cubes 0.3
Dyadic interpolation scheme 5.1
Dyadic martingales 0.3 7.1
Dyn 5.2
Eirola 4.3
entropy 9.2 9.3
Esteban 0.4 8.2
Euler — Frobenius polynomials 5.3
Evangelista 5.2
Evans 10.2
Extremal phase 5.2
Faber 5.2
Farge 0.2
Fast Wavelet Transform 0.4 8.2
Feauveau 0.5 5.4 7.1
Fefferman 6.3
Folded wavelet basis 8.3
Fourier transform 1.1
Fourier windows 0.1 1.3 9.3 9.4
Fractional derivation, integration 2.2 2.5
frames 0.2 1.2 2.1 2.5 7.1
Franklin 5.2
Franklin system 5.2
Frazier 0.3 2.6 6.3
Frisch 0.2 0.5
Functional analysis 0.3 6.1
Fundamental scaling function 4.4
Gabor 0.1 1.3
Gabor wavelets 0.1 1.3
Galand 0.4 8.2
Gaussian functions 0.1 7.1
Gerver 10.4
Goldberg 6.3
Goodman 6.3
Gram operator 1.2
Gripenberg 2.5 6.2
Groechenig 2.1 7.2 7.3
Grossmann 0.2 0.3 2.6
Haar 5.2
Haar basis 0.3 5.2 6.3 7.1 10.3
Half polynomials 8.3
Hardin 9.1
Hardy 10.4
Hardy space, 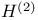 -analytic 0.2 3.4 -analytic 0.2 3.4
Hardy space, 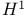 1.5 6.3 10.1 10.2 1.5 6.3 10.1 10.2
Hardy space, 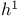 -local 6.3 -local 6.3
Hardy space, 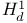 -dyadic 6.3 -dyadic 6.3
Hardy space, 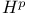 , , 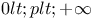 0.4 2.6 5.2 0.4 2.6 5.2
Heisenberg Inequality 0.1 1.1
Herley 5.2
Herrmann 0.5
Herve 4.2 4.3 9.1
Hoelder space 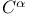 1.5 2.6 7.3 see \infty}_{\infty} \alpha\notin\mathbf{N}$"/>" 1.5 2.6 7.3 see \infty}_{\infty} \alpha\notin\mathbf{N}$"/>"
Holladay theorem 5.3
Holschneider 1.6 8.1 10.4
Instantaneous frequency 0.1
Interpolating scaling function 5.1
Interpolating scaling function with minimal support 5.1
interval 8.3
Irregular sampling theorem 2.1
Jacobi function  10.4 10.4
Jaffard 0.3 1.6 6.6 7.1 10.4
Jawerth 0.3 2.6 6.3
Jia 7.2
Johnstone 8.6
Joint resolution 1.4
Jones, L.K. 9.4
Jones, P. 10.3
Jouini 8.3
Journe 0.5 3.3 10.1 10.3
| Kessler 9.1
Klauder 0.2
Kronland-Martinet 0.2 8.1
Lacunary Fourier series 1.6
Lagrangian interpolating spline function 5.3
Lam 7.2
Laplacian pyramidal algorithm 0.4 0.5 8.2
Latto 8.4
Lebesgue space  2.6 5.2 6.2 7.3 2.6 5.2 6.2 7.3
Lebesgue space  , weighted 6.4 , weighted 6.4
Lee 9.1
Lemarie-Rieusset 0.4 3.2 3.4 5.2 5.3 6.4 6.5 7.1 7.2 8.3 8.4
Linear phase 0.5 5.2 5.4
Lions 10.2
Littlewood — Paley decomposition 0.3 2.6
Littlewood — Paley multiresolution analysis 3.3 5.1 5.2
Littlewood — Paley — David wavelet 3.3
Littlewood — Paley — Meyer wavelet see "Meyer — Lemarie wavelet"
Littlewood — Paley — Stein theory 7.3
Local multiresolution analysis 4.4
Local regularity 6.6
Local sine basis 0.5 9.3
Low 1.6
Lusin area integrals 0.3
Maday 7.1
Madych 7.1 7.3
Malgouyres 4.3 4.4 5.2
Mallat 0.4 3.3 5.2 9.4
Mallat algorithm 0.4 8.0 8.2 9.2
Malvar 0.5 9.3
Malvar window 9.3
Marr 7.1
Massopust 9.1
Matching pursuit algorithm 9.4
Maximally flat filters 0.5
Merging property 9.3
Mexican hat 7.1
Meyer 0.0 0.3 0.4 0.5 1.6 2.2 2.6 3.3 4.4 5.1 5.2 6.1 6.4 6.5 6.6 7.1 7.2 7.3 8.3 9.2 9.3 10.1 10.2 10.4
Meyer — Lemarie wavelet 0.3 0.4 3.3 5.2 6.5 7.2
Micchelli 7.2
Microlocal space 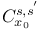 6.6 10.4 6.6 10.4
Minimal support 4.4
Molecule 6.3 6.5
moment 8.4
Morlet 0.1 0.2 1.4 2.1 8.1
Morlet wavelet 0.1 0.2 1.4 2.1 2.6
Morlet wavelet, multivariate 7.1
Muckenhoupt weights 6.4
Multifractals 0.3 0.5 10.4
Multiresolution analysis 0.4 3.3 4.1 7.1
Multiresolution analysis,  -localized 4.1 -localized 4.1
Multiresolution analysis, bi-orthogonal 3.3
Multiresolution analysis, generalized 3.3
Multiresolution analysis, local 4.4
Multiresolution analysis, multiple 9.1
Multiresolution analysis, regular 4.1
Multiscale analysis 0.2
Multivariate wavelets 7
Murenzi 7.1
Non-stationary multiresolution analysis 5.2
Non-stationary signals 9.4
Normalization of a scaling filter 5.2
Novikov 5.2
Orthonormal wavelets, multiresolution analysis, scaling function 0.3 0.5 5.2 8.2 see "Daubechies "Meyer "Stroemberg
Paradifferential operators 0.3 2.6
Paraproducts 10.1
Paul 0.2
Periodic wavelets 8.3
Phase 5.2 5.4
Pittner 0.5
Pointwise regularity 1.6 6.6
Polyharnomic splines 7.1
Polynomial scaling filter 0.5 4.4
Pre-wavelets 5.3
Primitive of a scaling function 4.2 8.4
Projection operators 3.1 3.2 3.4 6.1
Pseudodifferential operators 8.5
Quadrature formulae 8.4
Quadrature mirror filters 0.4 0.5 8.2
Quake 9.2
Quillen — Suslin theorem 7.2
Rational dilation factor 3.2 3.3
Rational filter 5.2
Regular sampling theorem 2.1 7.1
Regularity of the scaling function 4.2 4.3
Reproducing formula 1.2
Resolution 1.1 1.3
Reznikoff 8.4
Ridge and skeleton extraction algorithm 0.2 10.4
Riemann 10.4
Riemann — Weierstrass function 10.4
Riemenschneider 7.1
Riesz basis 1.2
Riesz lemma 0.5 5.2
Rioul 5.2
Rokhlin 0.3 8.4 8.5
RON 5.2
Rvachev function 5.2
Scaling filter 0.4 4.1 4.2
Scaling function 0.4 4.1
Scaling function,  -localized 4.1 -localized 4.1
Scaling function, compactly supported 4.4
Scaling function, fundamental 4.4
Scaling function, interpolating 5.1
Scaling function, regular 4.1
Schaeffer 0.2
Schauder 5.2
Schneid 0.5
Schoenberg 5.3
Self-similar tilings 7.3
Semmes 10.2 10.3
Separable wavelets 7.1
Separation lemma 4.4
Shen 7.1
Shi 2.1 3.4
Shift-invariant spaces 3.1 7.2
Short wavelets 9.1
Short-Time Fourier Transform 0.1 see
smith 0.4
Sobolev spaces 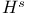 1.5 2.5 2.6 5.2 7.3 see 2}_{2}$"/>" 1.5 2.5 2.6 5.2 7.3 see 2}_{2}$"/>"
Spline Function 5.3
Spline function with multiple knots 9.1
Spline wavelets 0.4 5.2 5.3 5.4
Stegers 1.6
Stein 0.3 6.1 6.3 7.3
Strang — Fix conditions 0.5 5.2
Stroemberg 0.4 5.2 5.3
Stroemberg spline wavelet 5.2 5.3
Subband coding scheme 0.4 8.2 9.2
Sweldens 8.4
Symmetric scaling function 8.3
Tabulation of a scaling function 8.4
Tang 9.1
Tchamitchian 0.2 1.6 10.4
Tenenbaum 8.4
Tensor product of multiresolution analyses 7.1
Tight frame 1.2
Time-frequency analysis 0.1
Time-frequency atoms 9.4
Torresani 0.2 10.4
Transition operator 4.2 4.3 4.4 5.1
Turbulence 0.2
Two-scale difference equation 4.1 8.4
Ueberhuber 0.5
Unconditional basis 6.1
Vaguelettes lemma 2.2 7.1
Vetterli 5.2
Vial 8.3
Ville 0.1
Villemoes 4.3 7.3
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



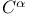 (Hoelder space)
(Hoelder space) 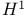 (Hardy space)
(Hardy space) 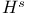 (Sobolev space)
(Sobolev space) 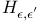

 -transform
-transform 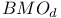 , bmo
, bmo 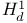
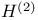 -analytic
-analytic 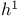 -local
-local 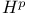 ,
, 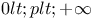

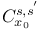
 -localized
-localized