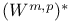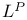|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ziemer W.P. — Weakly Differentiable Functions: Sobolev Spaces and Functions of Bounded Variation |
|
|
 |
| Предметный указатель |
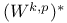 , measures contained within 4.7(205) , measures contained within 4.7(205)
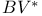 , and measures 5.12(266) , and measures 5.12(266)
 -measurable set 1.2(6) -measurable set 1.2(6)
 domains 2.5(64) domains 2.5(64)
(K, p)-extension domain 2 5(63)
Absolute continuity on lines 2.1(44)
Absolutely continuous measures 1.3(15)
Adams, David 2.9(92) Historical
Admissible domain 5.10(256)
Approximate limit, lower 5.9(250)
Approximate limit, upper 5.9(250)
Approximate tangent plane Historical Notes 5(218)
Approximately continuous 5.9(250)
Aronszajn — Smith Historical Notes 2(108)
Banach Indicatrix formula 2.7(76)
Banach space 1.5(21)
Beppo Levi Historical Notes 2(108)
Besicovitch covering theorem 1.3.6(12)
Besicovitch differentiation theorem 5.8(248)
Besicovitch, A, S. Historical Notes 1(40)
Bessel capacitability, Suslin sets 2.6(71)
Bessel capacity 2.6(66) 4.5(194)
Bessel capacity and Hausdorff measure 2.6(75)
Bessel capacity, and maximal functions 3.10(154)
Bessel capacity, as outer measure 2.6(67)
Bessel capacity, inner regularity 2.6(72)
Bessel capacity, metric properties 2.6(73)
Bessel kernel 2.6(65)
Bessel potentials, and Sobolev functions 2.6(66)
Blow-up technique 5.6(237)
Borel measure 1.2(6)
Boundary, of a set 1.1(1)
Boundary, of a set, measure-theoretic 5.8(249)
Boundary, of a set, reduced 5.5(233)
Bounded variation, on lines 5.3(227)
Boxing inequality 4.9(218)
Brelot 2.6(68)
Brezis — Lieb Historical Notes 2(110)
Brezis — Wainger 2.9(91) Historical
Burago — Zalgaller Historical Notes 1(41)
BV function, extension of 5.10(257)
BV function, trace of 5.10(258)
BV functions 2.1(43) 5.1(220)
BV functions, and capacity 5.12(262)
BV functions, and co-area formula 5.4(231)
BV functions, and Poincare inequality 5 11(261)
BV functions, approximation by smooth functions 5.3(225)
BV functions, compactness in  of unit ball 5.3(227) of unit ball 5.3(227)
BV norm 5.1(221)
Caecioppoli, R. Historical Notes 5(281)
Calderdn — Stein 2.5(64)
Calderon Zygmund Historical Notes 3(175)
Calderon, A.P. Historical Notes 3(175}
Calderon, A.P., lemma 1.8(36}
Calkin, H. Historical Notes 2(108)
Capacity and BV functions 5.12(262)
Capacity and Hausdorff measure 5.12(265)
Capacity, inner regularity 5.12(263)
Capacity, regularity of 5.12(267)
Caratheodory, C Historical Notes 1(41)
Cartan, H. Historical Notes 2(109)
Cauchy’s inequality 1.5(19)
Cesari, L. Historical Notes 5(280)
Chain rule, Sobolev functions 2.1(48)
Change of variable, Sobolev functions 2.1(52)
Characteristic function of a set 1.1(2)
Choquet, G. 2.6(70)
Closed ball 1.1(2)
Co-area formula 2.7(76) 4.4(192) 4.9(210)
Co-area formula, for BV functions 5.4(231)
Co-area formula, general formulation 2.7(81)
Continuity of Bessel capacity 2.6(69)
Continuous functions, space of 1—1(2)
Convolution of distributions 1.7(25)
Convolution of functions 1.6(21)
Countably rectifiable sets 5.7(243)
Countably rectifiable sets, and 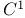 sub-manifolds 5.7(243) sub-manifolds 5.7(243)
Countably rectifiable sets, and Lipschitz maps 5 7(243)
DeGiorgi, E. Historical Notes 5(281)
DeGuzman, M. Historical Notes 1(41)
Deny, J. Historical Notes 2(109)
Difference quotients, bounded in  3.6(137) 3.6(137)
Distance function 1.1(1)
Distance function, smooth approximant 3.6(136)
Distance to a set 1.1(1)
Distribution function 1.8(26)
Distribution, derivative of 1.7(25)
Distribution, integrable function 1.7(24)
Distribution, multiplied by a function 1.7(25)
Distribution, Radon measure 1.7(24)
Distribution, Schwartz distribution 1.7(24)
Dual of 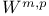 , representation 4.3(185) , representation 4.3(185)
Dual of 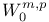 representation 4.3(187) representation 4.3(187)
Dual of Sobolev spaces 4.3(185)
Essential variation 5.3(227)
Exterior normal 5.5(233)
Exterior normal, generalized 5.5(233)
Exterior normal, measure-theoretic 5.6(240)
Federer, H. Historical Notes 5(281)
Finely continuous function 3.3 (123)
Finely covered set 1.3(8)
Finite perimeter, and countably rectifiable sets 5.7(243)
Finite perimeter, and relative isoperimetrie inequality 5.4(230)
Finite perimeter, containing smoothly bounded sets 5.4(229)
Finite perimeter, sets of 5 4(229)
Finite perimeter, sets of and Gauss — Green theorem 5.8(248)
Finite perimeter, sets of and Lipschitz domains 5.8(248)
Fleming Rishel Historical Notes 2(110) Historical
Fleming — Federer Historical Notes 2(110)
Frehse, J. Historical Notes 2(109)
Gagliardo, E. Historical Notes 2(109)
Gauss — Green Theorem 5.5(234)
Gauss — Green theorem, and sets of finite perimeter 5.8(248)
Gelfand, I.M. Historical Notes 1(41)
Generalized derivative 2.1(42)
Giusti, E. Historical Notes 5(281)
Goffman, C Historical Notes 5(281)
Gradient measure, continuity of 5.2(223)
Gradient measure, lower semicontinuity of 5.2(223)
Gradient of a function 1—1(2)
Guslin, W. Historical Notes 5(281)
Hahn — Banach theorem 4.3(186)
Hardt, Robert Historical Notes 1(40)
Hardy Littlewood — Wiener maximal theorem 2 8(84)
Hardy’s inequality 1.8(35)
Hausdorff dimension 1.4(18) Exercise
Hausdorff maximal principle 1.3(7)
Hausdorff measure 1.4(15)
Hausdorff measure, as an element of 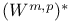 4.4(191) 4.4(191)
Hedberg Wolff Historical Notes 4(218)
Hedberg, Lars Historical Notes 2(111)
Holder continuous functions, space of 1.1(3)
Holder’s Inequality 1.5(20)
Hunt, R. Historical Notes 1(41)
Inner product 1.1(1)
Integral currents Historical Notes 5(281)
| Isodiametric inequality 1.4(17)
Isoperimetrie inequality 2.7(81)
Isoperimetrie inequality, relative 5.4(230)
Jensen’s Inequality 1.5(20)
Jessen — Marrinkiewicz Zygmund Historical Notes 1(40)
Jones, Peter 2.5(64)
K-quasiconformal mapping Historical Notes 2(108)
Kondrachov, V. Historical Notes 2(109)
Krickerberg, K. Historical Notes 5(280)
Kronrod, A.S. Historical Notes 2(110)
Lebesgue measurable set 1.2(3)
Lebesgue measure 1.2(3)
Lebesgue measure, as an element of 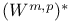 4.4(188) 4.4(188)
Lebesgue point and approximate continuity 4.4(190)
Lebesgue point for higher order Sobolev functions 3.3(122)
Lebesgue point for Sobolev functions 3.3(118) 3.10(157}
Lebesgue point of a Sobolev function 4.4(190)
Lebesgue point, arbitrary measures 1.3(14)
Lebesgue, H. Historical Notes 1(39)
Leibniz formula Exercise 1.5 (37)
Length of multi-index 1.1(2)
Lipschitz domain 2.5(64) 4.4(191)
Lorentz space, norm 1.8(28)
Lorentz spaces 1.8(28) 2.10(96)
Lorentz, G. Historical Notes 1(41)
Lorentz, G., at all points 3.9(152)
Lorentz, G., derivative 3.4(129)
Lorentz, G., difference quotients 2.1(46)
Lorentz, G., norm 1.5(18)
Lorentz, G., related to distributional derivatives 3.9(147)
Lorentz, G., spaces 1.5(18)
Lusin’s theorem for Sobolev functions 3.10(159) 3.11(166)
Marcinkiewicz interpolation theorem 4.7(199)
Marcinkiewicz space 1.8(28)
Maximal function 2.8(84)
Maximal function, fractional 4.7(204)
Maz’ya, V. Historical Notes 2(109) Historical
Measure densities 3.2(116)
Measure, with finite K, p-energy 4.7(204)
Median, of a function 5.12(269)
Meyers — Serrin Historical Notes 2(109)
Meyers — Ziemer Historical Notes 4(218) Historical
Meyers, Norman Historical Notes 4(217)
Michael — Ziemer Historical Notes 3(176)
Minimax theorem 2.6(72) 5.12(268)
Minkowski content 2.7(83)
Minkowski’s inequality 1.5(20)
Mollification 1.6(21)
Morrey, C.B. Historical Notes 2(109)
Morse — Sard theorem 2.7(81) 4.4(192)
Morse, A.P. Historical Notes 1(40)
Moser, J. 2.9(91)
Multi-index 1.1(2)
Nirenberg, L. Historical Notes 2(109)
Non-linear potential 4.7(205)
Non-tangential limits 3.9(147)
Norm of vector 1.1(1)
Open ball 1.1(2)
Outer measure 1.2(6)
Outer regularity of Bessel capacity 2.6(69)
O’Neil, R. Historical Notes 1(41)
Partial derivative operators 1.1(2)
Partial derivative, as a measure 5.1(220)
Partition of unity 2.3(53)
Poincare inequality, abstract version 4.1(179)
Poincare inequality, and BV functions 5.11(261)
Poincare inequality, and measures in (BV)* 5.12(266)
Poincare inequality, and median of functions 5.13(269)
Poincare inequality, extended version with Bessel capacity 4.6(198)
Poincare inequality, general version for Sobolev functions 4.2(183)
Poincare inequality, indirect proof 4.1(177)
Poincare inequality, with Bessel capacity 4.5(195)
Poincare inequality, with Hausdorff measure 4.4(191)
Poincare inequality, with Lebesgue measure 4.4(189)
Polya — Szego Historical Notes 1(41)
Projection mapping 4.1(178)
Rademacher, H. Historical Notes 2(108)
Rademacher’s Theorem 2.2(50)
Rademacher’s theorem in  3.8(145) 3.8(145)
Radon Historical Notes 1(39)
Radon measure 1—2(6)
Radon — Nikodym derivative 1.3(15)
Radon — Nikodym derivative, and differentiation of measures 5.5(234)
Rearrangement, non-increasing 1.8(26)
Reduced boundary 5 5(233)
Regularization 1.6(21)
Regularization of BV functions 5 3(224)
Regularization of Sobolev functions 2.1(43)
Rellich — Kondrachov Compactness Theorem 2.5(62)
Rellich — Kondrachov imbedding theorem 4.2(182)
Resctnjak, S. Historical Notes 2(110)
Riesz capacity 2.6(66)
Riesz composition formula 2.8(88)
Riesz potential 2.6(64)
Riesz representation theorem 4.3(186)
Schwartz, L. Historical Notes 1(41)
Sigma algebra 1.2(3)
Sobolev Historical Notes 2(109)
Sobolev function 2.1(43)
Sobolev function,  approximation by Taylor polynomial 3.4(127) approximation by Taylor polynomial 3.4(127)
Sobolev function, approximate continuity of 3.3(122)
Sobolev function, fine continuity of 3.3(124)
Sobolev function, integral averages of 3.1(115)
Sobolev function, represented as a Bessel potential 4.5(194)
Sobolev inequality 2.4(56) 2.7(81)
Sobolev inequality, critical indices 2.9(89)
Sobolev inequality, critical indices in Lorentz spaces 2.10(98)
Sobolev inequality, for Riesz potentials 2.8(86)
Sobolev inequality, involving a general measure 4.7(199)
Sobolev inequality, relative to sub-manifolds 4.7(203)
Sobolev inequality, with general measure and p =1 4.9(209)
Steiner, J. Historical Notes 1(41)
Strichartz, R. Historical Notes 2(111)
Strong-type operator 4.7(199)
Suslinset 1.2(6)
Talenti, G. 2.7(82)
Taylor polynomial 3.4(126)
Thin sets 3.3(123)
Tonelli, L. Historical Notes 5(280) Historical
Total differentiability, Lipschitz functions 2.2(50)
Total variation measure 5.1(221)
Total variation, for functions 2.7(76)
Totally bounded set 2.5(62)
Trace of a Sobolev function 4.4(190)
Trace of a Sobolev function, of BV function in terms of integral averages 5.14(276)
Trudinger, N. Historical Notes 2(111)
Truncation of Sobolev functions 2.1(47)
Vitali, G. Historical Notes 1(40)
Vol’pert, A. Historical Notes 5(281)
Weak 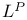 1.8(28) 1.8(28)
Weak derivative 2.1(42)
Weak-type operator 4.7(199)
Whitney extension theorem 3.5(131)
Whitney extension theorem,  version 3 6(141) version 3 6(141)
Whitney, H. Historical Notes 1(40)
Young’s inequality 1.5(20)
Young’s inequalityin Lorentz spaces 2.10(96)
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



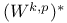 , measures contained within
, measures contained within 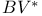 , and measures
, and measures  -measurable set
-measurable set  domains
domains  of unit ball
of unit ball 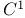 sub-manifolds
sub-manifolds 
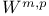 , representation
, representation 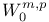 representation
representation