Yurinsky V. — Sums and Gaussian Vectors :: Электронная библиотека попечительского совета мехмата МГУ

Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск Форум

Авторизация

Поиск по указателям

Yurinsky V. — Sums and Gaussian Vectors

Обсудите книгу на научном форуме

Нашли опечатку?
Выделите ее мышкой и нажмите Ctrl+Enter

Название: Sums and Gaussian Vectors

Автор: Yurinsky V.

Аннотация:

Surveys the methods currently applied to study sums of infinite-dimensional independent random vectors in situations where their distributions resemble Gaussian laws. Covers probabilities of large deviations, Chebyshev-type inequalities for seminorms of sums, a method of constructing Edgeworth-type expansions, estimates of characteristic functions for random vectors obtained by smooth mappings of infinite-dimensional sums to Euclidean spaces. A self-contained exposition of the modern research apparatus around CLT, the book is accessible to new graduate students, and can be a useful reference for researchers and teachers of the subject.

Язык:

Рубрика: Математика/

Статус предметного указателя: Готов указатель с номерами страниц

ed2k: ed2k stats

Год издания: 1995

Количество страниц: 324

Добавлена в каталог: 05.07.2008

Операции: Положить на полку | Скопировать ссылку для форума | Скопировать ID

Предметный указатель

Average translation      166
Banach space, containing a basis      266
Banach space, type-2      266
Bergstrom expansion      173
Central projection      14
Characteristic functional (CF)      260
Characteristic functional (CF) of Gaussian RV      3 58 168
Characteristic functional (CF) of RV finite-dimensional distributions      261
Characteristic functional (CF) of RV finite-dimensional distributions, consistency condition      261
Characteristic functional (CF) of squared norm      209
Characteristic functional (CF) of squared norm for Gaussian RV      7 67
Characteristic functional (CF), smoothing inequality      179
Convex function, piecewise-linear      24
Convex function, piecewise-linear level sets      24
Convex function, stictly      20
Convex function, stictly level sets      20
Convex polytope      24
Convolution formula      259
Cramer condition      111
Cramer conjugate      111
Cramer transform      111
Cylindrical $\sigma$ -algebra      260
Cylindrical subsets      260
Deviation function on R      267
Deviation functional (DF)      124
Deviation functional (DF) of Gaussian RV      148
Deviation rate      125
Deviation rate and Kullback — Leibler information      139
distribution      258
Distribution, finite-dimensional of RV      261
Distribution, finite-dimensional of RV, consistency      261
Distribution, Gaussian in 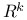$\mathbb{R}^k$       3
Distribution, Gaussian in 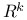$\mathbb{R}^k$ , nondegenerate      3
Distribution, Gaussian in 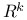$\mathbb{R}^k$ , standard      2
Distribution, Laplace transform of      111
Distribution, Radon      259
Distribution, standard normal      1
Distribution, tight      259
Distribution, uniform on sphere      7
Distribution, uniform on sphere, isoperimetric inequality      8
Edgeworth expansion      175 178 216
Expectation (in Banach space)      263
Focusing condition      221
Gaussian distribution in 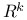$\mathbb{R}^k$       3
Gaussian distribution in 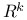$\mathbb{R}^k$ , characterization      4
Gaussian distribution in 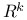$\mathbb{R}^k$ , covariance matrix      3
Gaussian distribution in 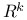$\mathbb{R}^k$ , nondegenerate      3
Gaussian distribution in 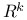$\mathbb{R}^k$ , standard      2
Gaussian distribution, centered in linear space      43
Gaussian random vector (RV), centered in linear space      43
Gaussian random vector (RV), in 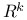$\mathbb{R}^k$       3
Gaussian random vector (RV), in 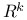$\mathbb{R}^k$ , CF      3

Gaussian random vector (RV), in 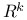$\mathbb{R}^k$ , distribution function      4
Gaussian random vector (RV), in 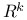$\mathbb{R}^k$ , standard      3
Gaussian random vector (RV), in Hilbert space      58
Gaussian random vector (RV), in Hilbert space, covariance operator      59
Gaussian random vector (RV), in Hilbert space, eigenbasis      59
Gaussian random vector (RV), in Hilbert space, principal eigenspace      59
Geodesic distance      8
Hilbert space, Chebyshev inequality in      79
Hilbert space, Gaussian RV in      58
Independent copies      258
Independent random elements      258
Kullback — Leibler information      132
Laplace method      223
Large deviations (LD)      123
Large deviations (LD) of normal distribution      1
Levy inequality      86
Measurable linear space      259
Measurable seminorm      44 80
Operator, covariance      59
Operator, covariance, resolvent      7 67
Operator, S-operator      267
Operator, trace      267
Ordered sum      107
Prokhorov theorem      259
Radon measure      259
Random element (RE)      258
Random element (RE), distribution      258
Random vector (RV)      259
Random vector (RV), Gaussian centered      43
Random vector (RV), Gaussian in 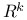$\mathbb{R}^k$       4
Random vector (RV), Gaussian in 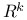$\mathbb{R}^k$ , joint DF of coordinates      4
Random vector (RV), Gaussian in 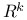$\mathbb{R}^k$ , Slepian inequality      4
Random vector (RV), Gaussian in Hilbert space      58
Random vector (RV), symmetrical      86
Random vector (RV), symmetrization      87
Random vector (RV), truncated      117
Relative entropy      132
S-topology      267
Slepian inequality      4
Smoothing inequality      179
Subadditive sequence      125
Surface area      257
Surface area, monotonicity      257
Surface integral      256
Symmetrization of RV      87
Tight measure      259
Uniform distribution on sphere      7
Uniform distribution on sphere, isoperimetric inequality      8
Uniform distribution on sphere, near normality of projections      9
Uniform integrable majorant      27
Weak convergence      259
Weak convergence, weak compactness      259
Weak convergence, weak compactness, criterion      259

О проекте