|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Wahlbin L.B., Dold A. (Ed), Takens F. (Ed) — Superconvergence in Galerkin Finite Element Methods |
|
|
 |
| Предметный указатель |
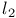 -projection 5 36 42 -projection 5 36 42
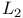 -projection, stability in -projection, stability in 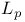 35 39 35 39
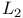 -projection, superconvergence in 42 -projection, superconvergence in 42
Approximation theory 30
Boundary element method 116
Bramble — Hilbert lemma 37
Computational domain 100
Delta-function, discrete 10 38
Delta-function, exponential decay in 10 39
Difference quotients 23 87 89 101 110
Difference quotients, maximum-norm estimates via on translation invariant meshes 92
Duality argument 31 50
Finite elements see also "Meshes"
Finite elements, Hermite cubics 1 16 27
Finite elements, intermediate degree (incomplete) 134
Finite elements, isoparametric 98
Finite elements, Serendipity 134
Finite elements, smoothest splines 1
Gauss points 81 82 133
Hermite cubics 1 16 27
Integral equation 25 116 121
Inverse estimates 7 28 37
Isoparametric elements 98
K-operator 107
Lagrange multiplier method 123
Leibniz' rule, discrete 91
meshes see also "Finite elements"
Meshes, Chevron pattern 125 133
Meshes, criss-cross pattern 47 125 133
| Meshes, quasi-uniform 2
Meshes, regular pattern 125 133
Meshes, symmetric w.r.t. a point 11 44 74
Meshes, tensor product 43 65 96 134
Meshes, translation invariant 84 98
Meshes, uniform 12
Meshes, Union Jack pattern 125 133
Minimal surface equation 95
Monotone 95
Multigrid 97
Negative norm estimates in 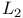 -projections 42 -projections 42
Negative norm estimates in elliptic projections 69
Newton's method 96
Outflow derivative 25 121
p-Laplacian 95
Physical domain 98
Principal lattice points 126
Quasiinterpolant 5
Quasiuniform meshes 2
Smoothest splines 1
Smoothing operator 32
Superapproximation 5 33 36
Superconvergence 3
Superconvergence, nodal 3
Symmetric meshes w.r.t. a point 11 44 74
Tensor product elements 43 65 96 134
Translation invariant spaces 84 98
Translation invariant spaces, maximum norm estimates via difference quotients 92
Uniform meshes 12
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



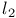 -projection
-projection 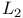 -projection, stability in
-projection, stability in