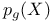|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Jannsen U. — Mixed Motives And Algebraic K-Theory |
|
|
 |
| Предметный указатель |
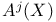 , , 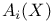 115 117 115 117
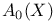 , Alb(X) 157 , Alb(X) 157
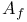 85 85
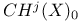 , , 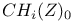 155 155
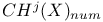 178 178
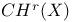 57 57
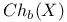 105 107 105 107
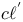 , , 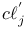 140 156 140 156
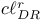 , , 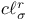 , , 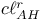 , , 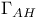 58 59 62 58 59 62
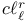 , , 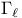 , , 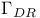 , , 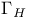 57 62 57 62
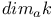 , L(V, s) 115 , L(V, s) 115
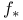 , , 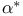 , , 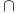 , , 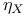 81 81
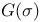 , , 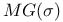 , , 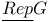 49 49
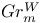 , , 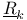 12 12
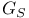 , , 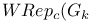 , , 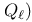 88 88
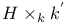 , , 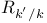 16 75 16 75
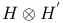 , , 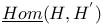 12 13 12 13
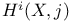 82 82
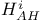 , , 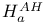 94 94
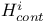 70 70
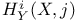 , , 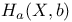 80 80
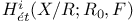 185 185
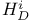 68 68
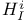 174 174
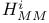 (= (=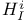 for for 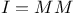 ) 180 ) 180
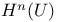 35 35
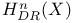 , , 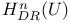 1 25 1 25
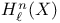 , , 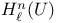 1 32 1 32
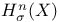 , , 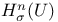 1 32 1 32
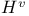 15 15
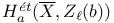 86 86
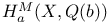 104 104
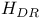 , , 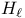 , , 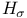 10 10
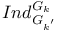 17 17
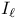 , , 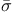 1 10 34 1 10 34
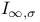 1 10 33 1 10 33
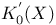 , , 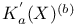 104 104
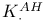 (Z.), (Z.), 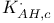 (Z.) 101 (Z.) 101
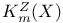 , , 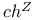 122 122
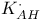 (X., Y.) 98 (X., Y.) 98
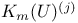 , , 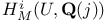 67 67
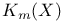 , , 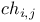 65 65
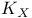 133 133
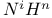 76 162 76 162
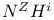 , , 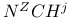 , , 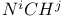 161 162 161 162
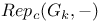 86 86
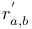 , , 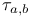 127 128 127 128
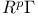 79 79
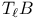 167 167
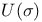 , , 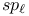 , , 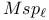 50 50
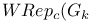 , , 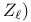 89 89
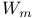 10 83 87 10 83 87
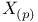 , div, tame 105 , div, tame 105
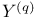 (two meanings) 27 76 (two meanings) 27 76
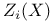 , , 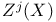 107 108 107 108
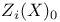 , , 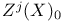 140 140
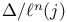 , , 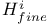 208 209 208 209
 14 81 125 14 81 125
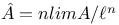 70 71 70 71
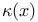 76 76
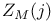 , , 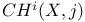 209 209
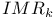 94 94
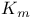 106 106
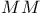 , , 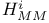 , , 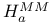 180 180
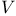 , , 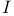 79 79
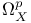 , ,  25 26 25 26
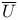 , , 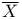 36 57 36 57
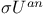 32 32
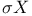 , , 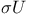 2 32 2 32
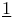 (identity object) 13 80 (identity object) 13 80
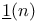 , H(n) 17 , H(n) 17
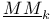 , , 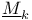 43 46 43 46
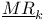 9 9
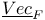 15 125 15 125
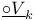 25 25
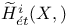 , , 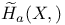 184 206 184 206
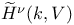 , , 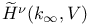 199 199
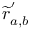 204 204
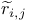 200 205 200 205
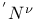 172 172
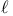 -adic (co)homology 1 4 32 36—40 69 86 89—90 97 101 115—117 126 149—151 172 184—186 191 215—219 -adic (co)homology 1 4 32 36—40 69 86 89—90 97 101 115—117 126 149—151 172 184—186 191 215—219
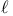 -adic (co)homology and motivic (co)homology 127 184 189—221 -adic (co)homology and motivic (co)homology 127 184 189—221
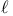 -adic Chern character 69 74 190 200 205 210 -adic Chern character 69 74 190 200 205 210
A-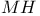 92 92
Abel — Jacobi map 140—143 151 153—178 183 204
Absolute (co)homology theory 153 174 182 183
Absolute Hodge cycle 3 14 59—65 72 73 127
Adams operators 67 104
Albanese variety 157—160 177
Algebraic cycle 57 107 108 115—121 139—141 155 165 168 170 173—180
Arithmetic 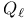 -representation, -sheaf 199 204 -representation, -sheaf 199 204
Arithmetical dimension 115—117
Artin motives 49 53
Base change 41 89 116 117 186 200 218
Base extension 16 75
Beilinson complexes 209
Beilinson conjecture on Chow groups 178—182
Beilinson/Bloch conjecture 158 168
Betti (co)homology 92
Birch and Swinnerton-Dyer 168 169
Bloch — Ogus theory see "Poincare duality theory"
Bloch's conjecture on zero cycles 177
Bloch's theorem on zero cycles 158
Bloch's theorem on zero cycles generalizations 170 182
Canonical filtration 28
Chern class, character 65 67—75 122—126 154 190 200 205 206 209 210 216
Chow group 57—59 105—107 109 118 121 122 154—182 189 204 212 220
Comparison isomorphism 1—5 11 14 33 34 40 41 58 59 65 97 126
Continuous etale cohomology 70 149—151 153
| CYCLE see "Algebraic cycle"
Cycle map 57—59 107—109 113 115 117 122 126 140 143 151—154 162 174 175 189 219
de Rham (co)homology 1 8 25 30 58 93 96 125
de Rham complex 25—31 96 97 101
Deligne (co)homology 68 69 131 132 152 153 182 183 186
Effective (Hodge structures or 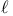 -adic representations) 172 -adic representations) 172
Extension class 139—143 150 176 180—183 204
Fibre functor 14 49 125
Filtration by coniveau 76 162—164 168—173 182 211
Filtration on Chow groups 178—182
Fundamental class 81 107 110 123 126
Galois descent 74 75 216
Geometric cohomology 129 153 177 183
Good proper cover 113 114 118 119 163
Grothendieck motive 180
Grothendieck — Riemann — Roch 122
Grothendieck/Serre conjecture 5 61 191
H 10 43 46
Higher Chow groups 209 212
Hodge conjecture classical 58 77
Hodge conjecture for arbitrary varieties 63 108 114
Hodge conjecture generalized (Grothendieck) 172
Hodge cycle 60 61 121
Hodge filtration 10 18 30 32 33 97
Hodge structure 1 58 172
Homologous to zero/homological equivalence 139 140 168 176 179
Identity object 13 80 83
Intermediate Jacobian 141 157
Internal hom 13
Intersection of cycles 174—178
K-cohomology 106 121
K-theory, 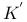 -theory 65 67—79 104—107 121—128 131—138 181 189 190 210 220 -theory 65 67—79 104—107 121—128 131—138 181 189 190 210 220
L-function 115—121 168 169 220
Level filtration 182
Lichtenbaum complexes 212
Linear varieties 217—221
Mixed 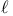 -adic sheaf 89—91 117 120 -adic sheaf 89—91 117 120
Mixed absolute Hodge complex 98—102
Mixed Hodge structure 10—13 32 34 64 92 93 100 141—143 152 186—188
Mixed motive 43—56 181—184 188
Mixed realization (for absolute Hodge cycles) of a smooth variety 35 55
Mixed realization (for absolute Hodge cycles) of an arbitrary variety 94—104 115 125 175 177 217
Mixed realization (for absolute Hodge cycles), abstract 9—24 43 94
Motive as defined by Grothendieck 180
Motive for absolute Hodge cycles 1—4 46—49 56
Motive, attached to a modular form 5—9
Motivic (co)homology 67 104—107 181 182 189 209—213 215 216
Motivic (co)homology and 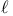 -adic (co)homology 127 184 189—221 -adic (co)homology 127 184 189—221
Motivic (co)homology and other (co)homology theories 126—130 154—156 182—184
Mumford — Tate group 61 62
Mumford's counterexample 157
Numerical equivalence 178—180
One-semi-simple 193 199
Parshin's conjecture 189
Poincare duality 3 8 45 82 108 118 128 134 140 190 215
Poincare duality theory (twisted) 79—107 121—126 173—176 182 186 194 208 210 214—216
Poincare duality theory (twisted) with weights 85 89 92 94 109—113 129 130 139 154—156 161 180
Potential 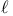 -adic sheaf 185 199 -adic sheaf 185 199
Projection formula 19 81 111 130 171
Pull back morphism (in homology) 215
Pure (of weight m) 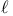 -adic representation/sheaf 87 116 -adic representation/sheaf 87 116
Pure (of weight m) Hodge structure 10
Pure (of weight m) object 83—85
Pure (of weight m) realization 12 15 46 63 64
purity 38 77 208 210
r, 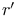 126 154 182 126 154 182
Realizations for absolute Hodge cycles 12 15 16 46 55 see
Realizations, attached to a modular form 5—9
Realizations, Betti (Hodge), de Rham, 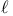 -adic and others 1 12 73 95 96 103 115 182—184 186 -adic and others 1 12 73 95 96 103 115 182—184 186
Regulator map 184
Representable 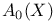 177 182 177 182
Resolution of singularities 25 56 93 95 112 114 191 192 194 195
Restriction 16 75
Riemann — Roch theorem 122 123
Riemann — Roch transformations 123—128 154 190 204 206
Roitman's theorems on zero cycles 157 159 160
Semi-simplicity 50 51 63 113 180 191—195 199 204 218 see
Simplicial variety 93 95—97 100—102 192
Smooth 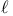 -adic sheaf 87 116 199 201 218 -adic sheaf 87 116 199 201 218
Specialization map 201—203 219
Spectral sequence, associated to a filtration 29
Spectral sequence, Bloch — Ogus 197
Spectral sequence, Brown — Gersten 106
Spectral sequence, Hochschild — Serre 70 143 150 151 153 203 206
Spectral sequence, hypercohomology/ext 144 151 152 180—183 211
Spectral sequence, Leray 32 41 185—187
Spectral sequence, Quillen 71 76 105 131 133 220
Standard conjectures 179 181
T(X), 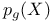 157 157
Tannakian category 14 15 43—56 61
Tate conjecture for arbitrary varieties 63 109 114 116—121
Tate conjecture, classical 57 77 115
Tate conjecture, generalized (Grothendieck) 172
Tate realization, object 17 181
Tate twist 2 17 18 58 92
Td(X), ch,  123 123
Tensor category 14 80 82 83 86 see
Tensor category with weights 83—85 88 92 94 180—183
Todd class 123—126
Twisted Poincare duality theory see "Poincare duality theory"
Variety 93
Weight see "Pure of weight m"
Weight filtration on (co)homology 30—32 89 92 97
Weight filtration on a mixed realization 10 12 94
Weight filtration on a tensor category 83 84
Weight filtration on an adic representation 87—91
Weight spectral sequence 30—43
Weights occurring in (co)homology 66 85 89 92 116 117
Weights occurring in an object 66 83
Weil cohomology 181
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



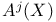 ,
, 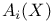
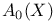 , Alb(X)
, Alb(X) 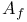
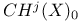 ,
, 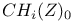
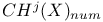
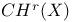
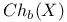
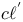 ,
, 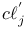
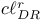 ,
, 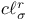 ,
, 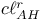 ,
, 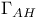
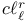 ,
, 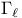 ,
, 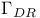 ,
, 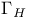
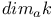 , L(V, s)
, L(V, s) 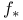 ,
, 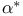 ,
, 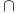 ,
, 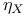
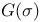 ,
, 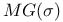 ,
, 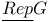
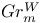 ,
, 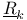
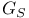 ,
, 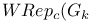 ,
, 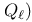
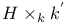 ,
, 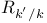
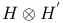 ,
, 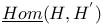
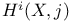
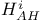 ,
, 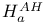
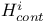
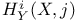 ,
, 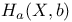
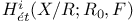
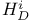
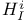
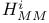 (=
(=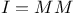 )
) 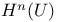
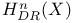 ,
, 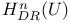
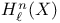 ,
, 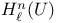
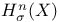 ,
, 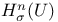
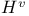
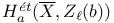
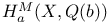
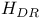 ,
, 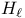 ,
, 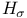
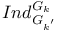
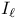 ,
, 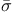
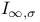
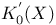 ,
, 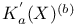
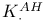 (Z.),
(Z.), 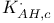 (Z.)
(Z.) 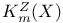 ,
, 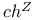
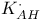 (X., Y.)
(X., Y.) 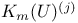 ,
, 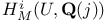
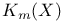 ,
, 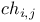
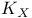
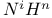
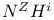 ,
, 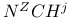 ,
, 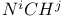
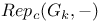
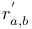 ,
, 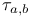
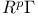
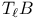
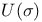 ,
, 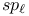 ,
, 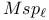
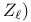
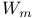
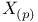 , div, tame
, div, tame 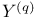 (two meanings)
(two meanings) 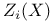 ,
, 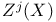
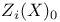 ,
, 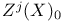
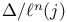 ,
, 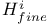

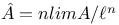
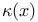
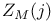 ,
, 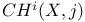
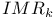
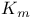
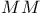 ,
, 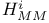 ,
, 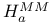
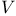 ,
, 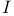
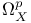 ,
, 
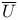 ,
, 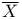
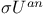
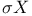 ,
, 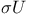
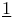 (identity object)
(identity object) 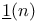 , H(n)
, H(n) 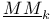 ,
, 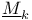
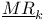
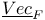
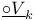
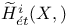 ,
, 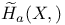
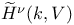 ,
, 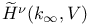
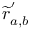
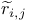
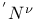
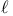 -adic (co)homology
-adic (co)homology 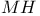
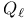 -representation, -sheaf
-representation, -sheaf 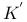 -theory
-theory