|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Courant R., Hilbert D. Ч Methods of Mathematical Physics, Vol. 2 |
|
|
 |
| ѕредметный указатель |
"Finite parts" of an integral 786
"Finite parts" of divergent integrals 740 743
"Improperly posed" problems 230 Ч 231
"Outward" derivative 134
"Tangential" differentiation; 577; see Interior differentiation TaylorТs theorem
"Weakly" space-like surface 654
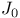 (BesselТs function of order zero) 694 (BesselТs function of order zero) 694
(F, G) pseudoanalytic function 386
A priori estimates see Estimates
AbelТs integral equation 535
Adjoint operators 234 Ч 237 770
Alfven speed 614
Alfven waves 613
Analytic function of two complex variables 501
Analyticity of harmonic functions 269
Analyticity of solutions of elliptic equations 501 Ч 505
Approximate progressing wave 623
ArzelaТs theorem 310 381
AsgeirssonТs mean value theorem 744 Ч 752
Associated Legendre functions 242
Asymptotic solutions for a linear hyperbolic system 637 Ч 642
Backward ray cone 564 569
Balayage method of Poincare 296 (ftn)
Banach space 333 403
Barrier function(s) 31
Barrier strong 341 Ч 343
Beltrami equations 178
Beltrami equations solution of 350 Ч 357
Bernstein, theorem of 400
Bessel equation 244
Bessel function(s) 194 289
Bessel function(s) integral theorem for 534
Bessel function(s) of order zero 185
Bicharacteristic rays 551 730
Bicharacteristic rays along multiple characteristics 627
Bicharacteristic rays differentiation along 597 Ч 599
Bicharacteristic strip(s) 558 583
Bicharacteristics (or bicharacteristic curves) 558 Ч 559
Bicharacteristics in hydrodynamics 601
Bicharacteristics invariance under transformation of independent variables of 562
Bicharacteristics of a second order differential equation 559
Bilinear form 770
Boundary continuity method 336 Ч 339
Boundary counter-example of Lebesgue 303 Ч 305
Boundary for general elliptic differential equations 320 Ч 331
Boundary for Poisson equation 261 ff
Boundary for the equation of minimal surfaces see PlateauТs problem
Boundary for the potential equation 21 Ч 22
Boundary in multiply-connected domains 292 293
Boundary nonlinear 395 Ч 399
Boundary space, maximal non-negative 658
Boundary uniqueness theorems for 320 Ч 324
Boundary value problem(s) 222 226 290 357
Boundary with nonunique solutions 324 Ч 326
Branch curves 65
Branch lines 408
Branch strip 415
Brouwer fixed point theorem 403
Calculus of variations 113 Ч 131
Canonical equations 131
Canonical form 182
Canonical perturbation theory 130 Ч 131
Canonical system of differential equations 107
Canonical transformation 127 Ч 129
Canonically conjugate variables 115
Capacity 305 Ч 306
Cauchy data 408
Cauchy double integral representation 501 (ftn)
Cauchy initial uniqueness of solutions 438 Ч 449
Cauchy initial value problem 407 Ч 766 (see also Initial value problem)
Cauchy method of the Fourier integral 210 Ч 221
Cauchy problems see Initial value problems
Cauchy Ч Kowalewski for linear equations 54
Cauchy Ч Kowalewski theorem 39 Ч 56 363 669 670
Cauchy Ч Riemann 176 178
Cauchy Ч Riemann differential equations 58
Caustic 673 674
Caustic curves 83 89
Caustic surface 123
Characteristic see also Bicharacteristic
Characteristic coordinates see Characteristics as coordinate curves
Characteristic, base curve(s) 63 70 411
Characteristic, basic manifold 138
Characteristic, condition 136 Ч 139 412 419 554 555
Characteristic, cone 591
Characteristic, cone, in HuyghensТ principle 690
Characteristic, curve(s) 29 70 158 172 407 411 415
Characteristic, curve(s), for the general first order differential equation in n independent variables 103 Ч 105
Characteristic, curve(s), on an integral surface 414 Ч 416
Characteristic, curve(s),for quasi-linear differential equations in n variables 69 70 73
Characteristic, derivative 136 Ч 139
Characteristic, determinant 172
Characteristic, differential equations, canonical form of 106 Ч 107
Characteristic, differentiation 135
Characteristic, element 410
Characteristic, form(s) 156 175 412 554 579
Characteristic, initial value problem(s) 56 450
Characteristic, initial value problem(s),of the wave equation 644 Ч 646
Characteristic, line element 33
Characteristic, matrix 173 530
Characteristic, normal cone 582 663
Characteristic, parameters 427 428
Characteristic, ray cone, for elastic waves 708
Characteristic, rays, of a second order equation 559
Characteristic, sheets, multiple 595 Ч 596
Characteristic, speed 430
Characteristic, strips 77 79 97 103 411 422
Characteristic, surface(s) 174
Characteristic, surface(s), as wave fronts 632
Characteristic, surface(s), in hydrodynamics 600 Ч 601
Characteristic, surface(s), in magnetohydrodynamics 613
Characteristic, surface(s), of a differential operator 579 Ч 581
Characteristic, surface(s), of a second order linear equation 557
Characteristic,condition, interpretation of, in time and space 581 Ч 583
Characteristics 55 Ч 56 170 175 553
Characteristics as branch elements 82
Characteristics, as coordinate curves 490 Ч 507
Characteristics, as curves of discontinuity 416 Ч 418
Characteristics, for quasi-linear systems 176
Characteristics, for second or er equations in two independent variables 408
Characteristics, geometry of 552 Ч 569
Characteristics, geometry, for higher order operators 577 Ч 599
Characteristics, invariance of 423 562 589
Characteristics, with constant multiplicity 626 Ч 627
ClairautТs equation 27 Ч 28 37 94
Classification for equations of second order 181 Ч 184
Compactness theorem for harmonic functions 275
Compatibility condition 60
Complete, integral 24 Ч 25 37 84 103
Complete, progressing wave 623
Complete, space 403
Compressible fluids 429 Ч 437
Compressible fluids, linearized equations 436 Ч 437
Cone 124 Ч 125 233
Conoid of dependence 654 730
Conservation, laws 147 Ч 153 488
Conservation, of energy 665
Conservative operators of first order 653
Consistency conditions for Cauchy data 472
Continuable initial conditions 470
Continuation of a real solution into the complex plane 499 Ч 507
Continuation of solutions 505
Continuity method 336
Continuous linear functional 771
Convex set 404
Convex, hull 589
Convex, hull,of a local ray cone 589 591
Convolution of ideal functions 791 Ч 792
Crystal optics 599 602 649
Crystal optics, conical refraction in 628 629
| Crystal optics, solution by method of plane mean values 718 Ч 727
Cylindrical waves 193 Ч 194
Damped waves 192
Darboux, differential equation for mean values 699 Ч 700
Darboux, equation 646 Ч 647
Darboux, equation, connection with the wave equation 700 Ч 703
Decomposition of ideal functions 781
Delta function 456 776
Delta function, as a weak limit 778
Delta function, decomposition of 730 Ч 733
Delta function, homogeneity 791
Delta function, in polar coordinates 791
Delta function, three dimensional 696
Delta function, transformations of 790 Ч 791
Derivative, directional 132
Derivative, normal 133
Descent, method of 205 Ч 206 686
Developable surfaces 10
Differentiability properties of solutions of boundary value problems 343 Ч 350
Differentiation of fractional order see Fractional differentiation
Dipole potentials 251
Dirac equations 179
Dirichlet, integral 254 681
Dirichlet, problem 261 Ч 264 (see also Boundary value problem GreenТs Poisson
Dirichlet, problem for general homogeneous elliptic equations 342
Discontinuities 585
Discontinuities, of solutions 486 Ч 490
Discontinuities, propagation of see also Transport equations
Discontinuities, propagation of, along rays 573 Ч 574
Discontinuities, propagation of, for first order systems 624 Ч 631
dispersion 191
Distributions 621 727 740 743 766
Domain of dependence 209 227 228 438
Domain of dependence, for crystal optics 723 Ч 727
Domain of dependence, for elastic wave equation 711
Domain of dependence, for hyperbolic equations 649 Ч 654 (see also Uniqueness theorems)
Domain of dependence, gaps in 726
Domain of dependence, in HuyghensТ principle 690
Domain of determinacy 439
Domain of influence 227 649
Double layer potential(s) 251 Ч 261 298 299
Dual cone see Normal cone
Dual, generating pair 386
Dual, spaces 793 796
Duhamel(Сs) integral 512 Ч 515 691
Duhamel(Сs) principle 202 Ч 204 668
Duhamel(Сs) principle, for systems of first order 204
Duhamel(Сs) representation for solutions of inhomogeneous problems 552
Duhamel(Сs) theorem 512 520
Dupin cyclides 763
Edge of regression 66
Edge of regression, of an integral surface 83
Eiconal 116 Ч 118
Eiconal, equation 123 (see also Hamilton Ч Jacobi equation)
Elastic constants 707
Elastic waves 706 Ч 711
Elimination from a linear system with constant coefficients 14 Ч 15
Elliptic 156 172 174 177 240
Elliptic, equations, transition to the hyperbolic case through complex domains 499 Ч 501
Elliptic, equations, uniformly elliptic 331 Ч 332
Elliptic, theta function 200
Energy conservation of see Conservation of energy flux
Energy, identities 662 Ч 663
Energy, inequalities 449 655 656 661 662
Energy, integral(s) 443 447 618 654 665
Energy, integral(s), for linear symmetric hyperbolic systems of first order 652 Ч 661
Energy, integral(s), for single second order equations 659
Energy, integral(s), method of 642
Equation of mixed type 161
Equicontinuous functions, lemma on the convergence of 310
Estimate(s) see also Energy inequalities HamackТs Maximum
Estimate(s), for solutions of Neumann problem 330 331
Estimate(s), for solutions of quasi-linear elliptic equations 359
Estimate(s), of Schauder 331 Ч 350
Estimate(s), of Schauder, for solutions of linear elliptic equations 331 Ч 336
Estimate(s), of Schauder, interior 333 Ч 335
Estimate(s), of Schauder, up to the boundary 335 Ч 336
Euler equations 114 Ч 115
Euler homogeneity relation 11
Existence of solutions, (quasi-linear equations) 357 Ч 362
Existence of solutions, of boundary value problems 336 Ч 341
Existence theorem(s) for solutions of partial differential equations see Cauchy- Kowalewsky theorem Holmgren
Existence theorem(s) of ordinary differential equations 30
Exponential operators 524
Extremal field 122
Factorial of a vector 577(ftn) 768
Families of functions, differential equations for 8 Ч 12
FermatТs principle 117
Field functions 116
First boundary value problem see Dirichlet problem Boundary
Fixed point method of Leray and Schauder 357 Ч 362
Foca, curves 76 83 86 89
Foca, strip 77 83
Focussing 673 Ч 674 736
Folium of Descartes 588
Forward ray cone 564 569
Fourier, integral 210ff
Fourier, transformation of ideal functions 793 Ч 795
Fractional differentiation 523 702
Fredholm integral equation method 299
Free, boundary problem(s) 225 Ч 226 348
Free, curve(s) 55 172
Free, initial surface for second order quasi-linear differential equations 554
Free, strip 410
Free, surface 173
Free, surface, for a differential operator 579
Fresnel surfaces 605
Functional see Linear functional
Fundamental solution(s) 184 Ч 187 727-
Fundamental solution(s), for elliptic equations 363 Ч 367
Fundamental solution(s), for single equations of second order 740 Ч 744
Fundamental solution(s), in crystal optics 723 Ч 726
Fundamental solution(s), of the heat equation 21
Fundamental solution(s), of the potential equation 244
Fundamental solution(s), of the reduced wave equation 314
Gaps, theorem on 736 Ч 737
GaussТ integral theorem 252 699
GaussТ integral theorem, for ideal functions 787 Ч 788
Generalized solution(s) 418 486 669
Generators 386
Geodesics on an ellipsoid 111 Ч 113
Geodetic distance 116 117 121 565
Geometrical optics, M 640 Ч 642
GreenТs formulas 252 Ч 258
GreenТs function 261 Ч 268 290 383
HaarТs uniqueness proof 145 Ч 147
HadamardТs conjecture 765
HadamardТs example of improperly posed problem 229
HadamardТs theory of hyperbolic equations 740
Hamilton Ч Jacobi equation 118
Hamilton Ч Jacobi equation, for geodetic distance 109
Hamilton Ч Jacobi equation, theorem 127 129
Hamiltonian function 106
Hamiltonian function, for the two body problem 109
Hankel function 194
Harmonic function(s) 240
Harmonic function(s), regular 241 244
HarnackТs inequality 269
HarnackТs theorem 273
Heat equation 20 Ч 22 154 188 217
Heat equation, initial value problems for 197 Ч 201 525
Heaviside function 622
Heaviside unit function see Unit function
Heaviside, calculus (Heaviside method of operators) 507 Ч 550
Heaviside, calculus (Heaviside method of operators), justification of 528 Ч 535
Heaviside, calculus (Heaviside method of operators), method 517 Ч 535
Heaviside, method of operators 508 517
Heaviside, operator, definition 528 Ч 529
Hilbert, invariant integral 125 Ч 126
Hilbert, space 668
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



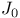 (BesselТs function of order zero)
(BesselТs function of order zero)