|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Alber H.D., Dold A. (Ed) — Materials with Memory: Initial-Boundary Value Problems for Constitutive Equations with Internal Variables |
|
|
 |
| Предметный указатель |
 -star-shaped 92 93 95 -star-shaped 92 93 95
Accretive operator 140
Associated free energy 26
Bingham, body 14
Bingham, law 14
Cauchy — Kowalevski, Theorem of 4
Causal mapping 139
Characteristic function 32
Classes of constitutive e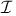 quations of quations of 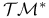 , , 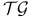 , , 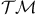 , ,  59 59
Classes of constitutive equations, definition of 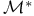 , , 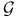 , , 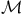 , , 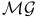 26 26
Clausius — Duhem inequality 145 146 147
Collapse theorem 29
Compatibility conditions 4 75 93 97 104
Complementary subspace, definition 77
Conservation law of energy 144
Conservation law of linear momentum 8 144
Conservation law of mass 144
Conservation law of moment of momentum 145
Crystallographic model 21 38
Deformation gradient 144
Dilatant 14
Dynamic problem 31
Elasticity tensor 8
entropy 145
Flow rule 11
Glide plain 21
Hardening 97 106ff 118
Hardening, isotropic 16ff
Hardening, kinematic 15ff
History functional, realization of 139
Hysteresis loop 142
Internal dissipation, inequality of 150
Korn's first and second inequalities 48 54
Lax — Milgram, Theorem of 54
Legendre transform 150 151 152
Material function 118
| Material objectivity, principle of 144
Monotone, maximal monotone, definition 26 27ff 31 45ff 59 100
Monotone, monotone operator, definition 24
Monotone, monotone vector field, definition 24
Norton's law 14
Proper function, definition 25
Pseudo-plastic 14
Quasi-static problem, definition 29
Set-valued map, domain of 10
Set-valued map, inverse of 50
Set-valued map, range of 50
Shakedown theorem 29
Simple material 144
Slip system 21
Sobolev spaces 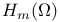 , , 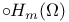 46 46
Star-shaped 92
Strain, strain rate 18 20
Strain, strain tensor, Green 144 152
Strain, strain tensor, inelastic 111
Strain, strain tensor, linear 8
Strain, strain tensor, macroscopic 21
Strain, strain tensor, plastic 8 11 13 20 21 107 117
Strain, strain tensor, viscous 13
Stress, backstress 15
Stress, deviator 12
Stress, overstress 20
Stress, stress tensor, Cauchy 7
Stress, stress tensor, Piola — Kirchhoff 144 145
Subdifferential, definition 25
Thermodynamically admissible 9
Transformation  of pairs, definition 58 of pairs, definition 58
Weak divergence 46 53
Weak formulation of initial-boundary value problems 47 56
Weak Neumann boundary condition 47 53 55
Yield criterion, Tresca's 12
Yield criterion, von Mises 11
Yield surface 99 100
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -star-shaped
-star-shaped  quations of
quations of 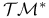 ,
, 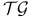 ,
, 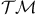 ,
, 
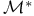 ,
, 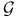 ,
, 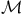 ,
, 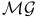
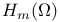 ,
, 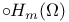
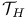 of pairs, definition
of pairs, definition