|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Lorentz R.A. — Multivariate Birkhoff Interpolation |
|
|
 |
| Предметный указатель |
Abel matrix 15
Almost regular, multivariate 10
Almost regular, univariate 3
Birkhoff interpolation scheme, multivariate 8
Birkhoff interpolation scheme, univariate 3
Class of a shift 48
Coalescence 57
Coefficient of collision 59
Collision of nodal matrices 48
Globally 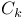 29 29
Hermite interpolation of tensor-product type 22
Hermite interpolation of type total degree 21
Hermite interpolation, univariate 5
Hermitian, nodal matrix 61
Hermitian, subset of 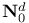 61 61
Image of a shift 48
Incidence matrix, multivariate 8
Incidence matrix, univariate 3
Line of a nodal matrix 53 59
Maximal coalescence 57
Maximal shift 49
Minimal coalescence 57
Minimal shift 49
Multiple shift 48
Multiplicity of a singularity 103
Nodal matrix 59
| Normal incidence matrix, multivariate 10
Normal incidence matrix, univariate 3
Order of a shift 48
Order regular 4
Polya condition, multivariate 15
Polya condition, univariate 5
Precoalescence 57
Pyramidal numbers 40
Regular at Z 10
Regular, multivariate 10
Regular, univariate 4
Shift 48
Signed number of shifts 36
Simple shift 48
Singular, multivariate 10
Singular, univariate 4
Singularity 103
Support of a nodal matrix 11
Tetrahedral numbers 40
Triangular numbers 36
Uniform Hermite interpolation of tensor-product type 23
Uniform Hermite interpolation of type total degree 22
Unique class of shifts 48
Unique shift 48
Upper set 15
Vandermonde determinant 9
Vandermonde matrix 9
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте