Kajitani K. — Hyperbolic Cauchy Problem :: Электронная библиотека попечительского совета мехмата МГУ

Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск Форум

Авторизация

Поиск по указателям

Kajitani K. — Hyperbolic Cauchy Problem

Обсудите книгу на научном форуме

Нашли опечатку?
Выделите ее мышкой и нажмите Ctrl+Enter

Название: Hyperbolic Cauchy Problem

Автор: Kajitani K.

Аннотация:

The approach to the Cauchy problem taken here by the authors is based on theuse of Fourier integral operators with a complex-valued phase function, which is a time function chosen suitably according to the geometry of the multiple characteristics. The correctness of the Cauchy problem in the Gevrey classes for operators with hyperbolic principal part is shown in the first part. In the second part, the correctness of the Cauchy problem for effectively hyperbolic operators is proved with a precise estimate of the loss of derivatives. This method can be applied to other (non) hyperbolic problems. The text is based on a course of lectures given for graduate students but will be of interest to researchers interested in hyperbolic partial differential equations. In the latter part the reader is expected to be familiar with some theory of pseudo-differential operators.

Язык:

Рубрика: Математика/

Статус предметного указателя: Готов указатель с номерами страниц

ed2k: ed2k stats

Год издания: 2008

Количество страниц: 180

Добавлена в каталог: 02.07.2008

Операции: Положить на полку | Скопировать ссылку для форума | Скопировать ID

Предметный указатель

Almost analytic extension      I-5 10
Bicharacteristic      II-6.1 6.2
Bicharacteristic, incoming, outgoing      II-6.1
Calderon — Vaillancourt inequality      II-3.1
Cauchy problem in $C^{\infty}$ classes      II-1.1 4.5 5.1 5.2 7.2 Appendix
Cauchy problem in $C^{\infty}$ classes in Gevrey classes      I-1 8 9
Characteristic of order r      II-1.1 1.2
Characteristic of order r, doubly      II-1.1 1.2 6.1 6.2 7.2
Characteristic of order r, multiple      II-5.2
Characteristic of order r, simple      II-1.1 6.1
Energy estimates      II-2.2 4.1 4.2 4.3 4.4 4.5 7.2
Euler's identity      II-3.2 7.1
Finite propagation speed      II-5.2 7.2
Finite propagation speed of wave front sets      II-5.2 7.2 Appendix
Fourier transform      I-1 6
Fourier transform, integral operator      II-Appendix
Fourier transform, integral operator with complex-valued phase function      I-5 6 8
Frobenius theorem      I-7.1
Gevrey classes      I-1 6 7 8
Hamilton (vector) field      II-1.1 6.2
Hamilton (vector) field, generalized flow      I-1 9 11
Hamilton (vector) field, map      II-1.1 6.1 7.1
Hoermander's condition      I-8
Hyperbolic polynomial      I-2 II-1.1
Hyperbolic polynomial, 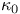$\kappa_{0}$       I-1 4 8 10
Hyperbolic polynomial, (or hyperbolicity) cone      I-1 II-1.1 1.2 2.1
Hyperbolic polynomial, effectively      II-1.1 1.2 2.1 4.1 5.2 6.1 7.1 7.2
Hyperbolic polynomial, strictly      I-1 8 II-Appendix
Inner semi-continuity (of hyperbolic cone)      I-2
Interpolation theorems      I-3 4
Linearity space      II-1.1 1.2
Localization (polynomial)      I-1 2 10 II-1.1 3.2 6.2

Loss of derivatives      II-5.2 7.2 Appendix
Malgrange's preparation theorem      I-1 II-1.1 3.2 6.2
Melin's inequality      II-4.2 4.4 7.2
Multiplicity of localization      I-2 4
Nuij's approximation      I-9
Parametrix in Gevrey classes      I-7 8 10
Parametrix in Gevrey classes with finite propagation speed of WF      I-3.1 3.2 5.2 7.2 Appendix
Poisson bracket      I-2.1 4.1 4.3 7.1
Principal part      I-1 4 8 9 10
Principal part, symbol      II-1.1 1.2 2.2 3.2 4.5 5.2 6.1 6.2 7.2
Propagation cone      I-1 II-1.1 1.2 6.1
Propagation cone of singularities      I-1 II-5.1 6.1 6.2
Propagation cone of wave front sets in Gevrey classes      I-4 10
Pseudo-differential operator      II-2.2 3.1 5.2 Appendix
Pseudo-differential operator in Gevrey classes      I-5 6 7
Pseudo-differential operator, classical      II-1.1 3.2 5.2
Pseudo-local property in Gevrey classes      I-7
Regularizing operator in Gevrey classes      I-6 7 10
Rellich's lemma      I-2
Sharp Garding inequality      II-5.1
Slowly varying, $\sigma$ -temperate metric      II-3.1
Smoothing operator      II-6.2
Stokes' formula      I-6
Subprincipal symbol      II-3.2 4.4 4.5 5.1 5.2 7.2
Symbol of spatial type      II-5.1
Symbol of spatial type, $\sigma$ , g-temperate      II-3.1
Symbol of spatial type, elliptic      I-6 II-6.2 Appendix
Symbol of spatial type, reversed      I-6
Symplectic 2-form      II-1.1
time function      II-1.1 1.2 2.1 5.1 6.2 7.1
Wave front sets in Gevrey classes      I-1 7 10
Weierstrass preparation theorem      I-2
Weight (function)      I-8 II-3.1

О проекте