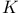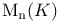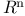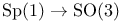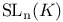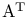Tapp K. — Matrix Groups for Undergraduates :: Электронная библиотека попечительского совета мехмата МГУ

Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск Форум

Авторизация

Поиск по указателям

Tapp K. — Matrix Groups for Undergraduates

Обсудите книгу на научном форуме

Нашли опечатку?
Выделите ее мышкой и нажмите Ctrl+Enter

Название: Matrix Groups for Undergraduates

Автор: Tapp K.

Аннотация:

Kapp argues that students should study matrix groups because they are integral to many areas of math, physics, and programming including topology, the theory of differential equations, quantum computing, and movie graphics. Assuming a background in calculus and in linear and abstract algebra, he prepares undergraduates for more advanced courses. The text include exercises. There's no indication of the author's academic affiliation.

Язык:

Рубрика: Математика/

Статус предметного указателя: Готов указатель с номерами страниц

ed2k: ed2k stats

Год издания: 2005

Количество страниц: 166

Добавлена в каталог: 02.07.2008

Операции: Положить на полку | Скопировать ссылку для форума | Скопировать ID

Предметный указатель

Action of a matrix group on $\mathbb{R}^\mathrm{m}$       118
Adjoint action      118
Affine group, $\mathrm{Aff}_\mathrm{n}(\mathbb{K})$       49
Alternating group      46
Ball      52
Block-diagonal matrix      141
Boundary point      52
Bounded      60
Campbell — Baker — Hausdorff Series      125
Cauchy sequence      55
Center of a matrix group      136
Central subgroup      132
Chain rule for Euclidean space      96
Chain rule for manifolds      108
Change of basis matrix      19
Clopen-both open and closed      59
Closed set      53
Commutative diagram      25
Compact      60
Complex numbers, $\mathbb{C}$       8
Complex structure      27
Complex-linear real matrices      26
Conjugate of a quaternion      10
Conjugate-transpose of a matrix, A*      36
continuous      57
Convergence of a sequence in $\mathbb{R}^\mathrm{m}$       55
Convergence of a series in 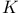$\mathbb{K}$       79
Convergence of a series in 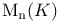$\mathrm{M}_\mathrm{n}(\mathbb{K})$       82
Convergence, absolute      80
Cramer's rule      18
Dense      56
Derivative of a function between manifolds      107
Derivative of a function from 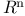$\mathbb{R}^\mathrm{m}$ to $\mathbb{R}^\mathrm{n}$       95
Derivative, directional      94
Derivative, partial      94
Determinant of a quaternionic matrix      31
Determinant of a real or complex matrix      13
Diffeomorphic      103
Dihedral group      45
Dimension of a manifold      104
Dimension of a matrix group      70
Discrete subgroup      139
Distance function on $\mathbb{R}^\mathrm{m}$       52
Division algebra      11
Double cover 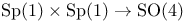$\mathrm{Sp}(1) \times \mathrm{Sp}(1) \to \mathrm{SO}(4)$       130
Double cover 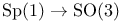$\mathrm{Sp}(1) \to \mathrm{SO}(3)$       126
Double cover, definition of      126
Double cover, others      130
Eigenvalue      147
Eigenvector      147
Euclidean space, $\mathbb{R}^\mathrm{m}$       51
Exceptional groups      159
Field      7
Frobenius      10
Fundamental domain      138
General linear groups, $\mathrm{GL}_\mathrm{n}(\mathbb{K})$       17
Graph of a function      111
Heine — Borel theorem      61
Hermitian inner product      34
Homeomorphism      58
Ideal of a Lie algebra      124
Identity component of a matrix group      110
Inner product on $\mathbb{K}^\mathrm{n}$       34
Integral curve      84
Inverse function theorem for Euclidean space      97
Inverse function theorem for manifolds      109
Isometry group of Euclidean space, $\mathrm{Isom}(\mathbb{R}^\mathrm{n})$       43
Isometry of 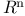$\mathbb{R}^\mathrm{n}$       41
Isometry of a matrix group      124
Lie algebra      68
Lie algebra homomorphism      115
Lie algebra isomorphism      115
Lie bracket      114

Lie correspondence theorem      125
Lie group      159
Limit point      55
Linear function      15
LOG      101
Manifold      104
Matrix exponentiation, $\mathrm{e}^\mathrm{A}$       83
Matrix group, definition of      63
Neighborhood      56
Norm of a quaternion      10
Norm of a vector in $\mathbb{K}^\mathrm{n}$       34
normalizer      162
Octonians      11
One-parameter group      89
Open cover      61
Open set      53
Orientation of $\mathbb{R}^\mathrm{3}$       42
Orthogonal      34
Orthogonal group, O(n)      36
Orthonormal      34
Parametrization      104
Path-connected      59
Poincare dodecahedral space      129
Polar decomposition theorem      66
Power series      80
Quaternionic-linear complex matrices      28
Quaternions      9
Radius of convergence      81
Rank      156
Real projective space, $\mathbb{RP}^\mathrm{n}$       128
Reflection      161
Regular element of a Lie algebra      161
Regular element of a matrix group      157
Regular solid      46
Riemannian geometry      123
Root test      81
Schwarz inequality      35
Skew-field      7
Skew-hermitian matrices, u(n)      75
Skew-symmetric matrices, so(n)      75
Skew-symplectic matrices, sp(n)      75
Smoothness of a function between subsets of Euclidean spaces      103
Smoothness of a function between two Euclidean spaces      95
Smoothness of an isomorphism between matrix groups      109
Special linear group, 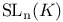$\mathrm{SL}_\mathrm{n}(\mathbb{K})$       39
Special orthogonal groups, SO(3)      5
Special orthogonal groups, SO(n)      39
Special unitary group, SU(n)      39
Sphere, $\mathrm{S}^\mathrm{n}$       6
Spin group      130
Sub-algebra of a Lie algebra      124
Sub-convergence      62
subspace      14
Symmetry group of a set, Symm(X)      45
Symmetry, direct and indirect      45
Symplectic group, Sp(n)      36
Symplectic inner product      35
Tangent bundle of a manifold      111
Tangent space      67
Topology of $\mathbb{R}^\mathrm{m}$       54
Topology of a subset of $\mathbb{R}^\mathrm{m}$       57
Torus in a matrix group      140
Torus of revolution      106
Torus, definition of      136
Torus, maximal      140
Torus, standard maximal      142
Trace of a matrix      12
Transpose of a matrix, 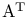$\mathrm{A}^{\mathrm{T}}$       12
Triangle inequality      52
Unit tangent bundle of a manifold      111
Unitary group, U(n)      36
Upper triangular matrices, group of, $\mathrm{UT}_\mathrm{n}(\mathbb{K})$       65
Vector field      73
Vector space, left      14

О проекте