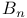Авторизация
Поиск по указателям
Humphreys J.E. — A Course in Group Theory
Обсудите книгу на научном форуме Нашли опечатку?
Название: A Course in Group TheoryАвтор: Humphreys J.E. Аннотация: This book is a clear and self-contained introduction to the theory of groups. It is written with the aim of stimulating and encouraging undergraduates and first year postgraduates to find out more about the subject. All topics likely to be encountered in undergraduate courses are covered. Numerous worked examples and exercises are included. The exercises have nearly all been tried and tested on students, and complete solutions are given. Each chapter ends with a summary of the material covered and notes on the history and development of group theory. The themes of the book are various classification problems in (finite) group theory. Introductory chapters explain the concepts of group, subgroup and normal subgroup, and quotient group. The Homomorphism and Isomorphism Theorems are then discussed, and, after an introduction to G-sets, the Sylow Theorems are proved. Subsequent chapters deal with finite abelian groups, the Jordan-Holder Theorem, soluble groups, p-groups, and group extensions. Finally there is a discussion of the finite simple groups and their classification, which was completed in the 1980s after a hundred years of effort.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1996Количество страниц: 304Добавлена в каталог: 01.07.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
214 213 216 217 218 214 Additive notation 6 Associativity axiom 1 Aut(G) 70 Automorphism 70 Automorphism, inner 73 Basis 236 Central extension 177 183 Central product 117 Centraliser 90 95 Centre 67 75 155 Chief factors 137 Classification of groups vii Classification of groups with 109 Classification of groups with 95 195 238 Classification of groups with 195 Classification of groups with 12 elements 108 196 238 239 Classification of groups with 16 elements 239 Classification of groups with 18 elements 200 239 240 Classification of groups with 20 elements 201 240 Classification of groups with 21 elements 107 240 Classification of groups with 24 elements 110 241 Classification of groups with 27 elements 241 Classification of groups with 28 elements 201 242 Classification of groups with 2p elements 106 238 Classification of groups with 3 elements 26 Classification of groups with 30 elements 109 116 159 242 Classification of groups with 4 elements 26 Classification of groups with 6 elements 45 Classification of groups with 70 elements 201 Classification of groups with 8 elements 46 238 Classification of groups with p elements 44 195 238 Classification of groups with pq elements 195 Classification of groups, finite abelian 120 Closure axiom 1 Code 49 50 Code, error-correcting 49 Code, error-detecting 49 Code, Golay ternary 53 220 Code, ISBN 49 Code, minimum distance 51 Codeword 50 Codeword, weight 51 Commutator 148 Complex Lie algebra 230 Composition factors 137 conjugate 59 Conjugate, element 59 Conjugate, subgroup 59 Coset 38 Coset decoding table 54 Cyclic extension 177 186 Decoding 54 Dynkin diagram 230 Equivalence class 14 39 Extension 174 Field 125 FORM 223—228 Form, alternating 226 Form, bilinear 226 Form, Hermitian 224 Form, kernel 228 Form, matrix of 224 Form, non-degenerate 224 Form, non-singular 228 Form, quadratic 228 Form, sesquilinear 223 Form, symmetric 228 G-set 89 Generating relations 33 Generator matrix 52 Generators 33 Greatest common divisor 235 Group 1 Group, 3 Group, abelian 1 Group, abelian, elementary 126 Group, adjoint Chevalley 230 Group, alternating 83 222 Group, alternating A(n) 144 Group, alternating A(S) 140 Group, automorphism group of cyclic group of order p 192 Group, automorphism group of cyclic Group, automorphism group of group of order 193 Group, automorphism group of dihedral group d(3) 195 Group, automorphism group of elementary abelian p-group 193 Group, classical 223 Group, cyclic 2 34—36 44 238 Group, dihedral 4 34 195 198 238 Group, direct product 5 112 Group, direct product, external 113 Group, direct product, internal 113 Group, finite 1 Group, finite abelian 120—127 Group, finite abelian p- 122 Group, finite abelian, type 124 Group, finite simple 202 222 Group, general linear 203 Group, generalised quaternion 196 198 238 Group, hyperoctahedral 170 Group, infinite 1 Group, Janko 231 Group, k-transive permutation 218 Group, Mathieu 231 Group, monster 231 Group, nilpotent 156 Group, of Lie type 222 230 Group, orthogonal 228 Group, p- 100 Group, projective special linear 204 223 Group, S(n) 77 Group, S(X) 12 Group, simple 137 Group, soluble 146 Group, special linear 203 Group, sporadic 222 231 Group, sporadic simple 213 Group, Suzuki 231 Group, symplectic 226 Group, table 3 Group, twisted 230 Group, unitary 223 Homomorphism 68 Homomorphism, image 70 Homomorphism, kernel 70 Identity axiom 1 Inverse 10 Inverse axiom 1 Inverse, unique 18 Isomorphism 69 Linear independent 236 MAP 8 Map, bijective 8 11 Map, composite 9 Map, graph 13 Map, identity 10 Map, injective 8 Map, inverse 10 11 Map, isomorphism 13 Map, one-to-one 8 Map, onto 8 Map, surjective 8 Matrix 3 202 Matrix, unitary 224 Multiplicative notation 5 Normaliser 91 96 Orbit 91 Order of a group 41 Order of an element 24 42 orthogonal matrices 229 Parity check matrix 55 Partition 14 Permutable 43 Permutation 12 77 Permutation, cycle notation 77 Permutation, cycle type 84 Permutation, disjoint 78 Permutation, even 82 Permutation, k-cycle 78 Permutation, odd 82 Permutation, transposition 81 Powers 22 Presentation 33 Prime 44 Pullback 118 Quotient group 62 Relation 13 91 Relation, equivalence 14 Relation, reflexive 14 Relation, symmetric 14 Relation, transitive 14 Scalar matrices 204 Section 174 Sectional factor set 175 Semidirect product 163 Series 128—33 Series, chief 133 Series, composition 133 Series, derived 150 Series, isomorphic 129 Series, normal 128 Series, subnormal 128 Series, upper central 155 Spanning set 236 Stabiliser 90 Steiner system 220 Subgroup 30 39 Subgroup, characteristic 139 Subgroup, characteristically simple 139 Subgroup, commutator 149 Subgroup, derived 149 Subgroup, generated by X 32 Subgroup, maximal 156 Subgroup, normal 59 Subgroup, Sylow p- 98 Syndrome 55 Syndrome decoding table 56 Theorem, Cayley 86 Theorem, Correspondence 65 Theorem, first isomorphism 72 Theorem, First Sylow 99 Theorem, Fourth Sylow 102 Theorem, Homomorphism 71 Theorem, Jordan — Holder 128 134 Theorem, Lagrange 41 Theorem, Orbit — Stabiliser 92 Theorem, Schreier's Refinement 132 Theorem, Second Isomorphism 73 Theorem, Second Sylow 100 Theorem, Sylow 98 Theorem, Third Sylow 101 Transitive 214 Transvection 208 Well-defined 15 62 71 Witt index 229 Wreath product 167—73 Wreath product, permutation 170 Wreath product, regular 167
Реклама
 |
|
О проекте
|
|
О проекте



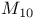

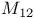
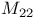 ,
, 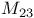 ,
, 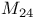

 elements
elements 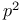 elements
elements 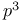 elements
elements