|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hasumi M. — Hardy Classes on Infinitely Connected Riemann Surfaces |
|
|
 |
| Предметный указатель |
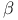 -dual IV.5C -dual IV.5C
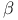 -topology IV.5B -topology IV.5B
(DCT), 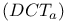 VII.3C IX.4A VII.3C IX.4A
Band II.5A
Behrens theorem X.7B
Betti number V.1A
Bishop theorem X.6C
Blaschke product IV.2C
Boundary m-function VIII.4A
Bounded characteristic II.5D XI.1B
Brelot — Choquet problem VI.5A
Bundle (unitary flat complex Line bundle) II.2A
Bundle of a multiplicative mero-morphic function II.2D
Bundle of an l.m.m. II.2C
Canonical basis I.2B
Canonical measure III.2B
Cauchy kernel I.11B
Cauchy theorem, direct VII.3C IX.4A
Cauchy theorem, direct Cauchy theorem, (weak type) VII.4B
Cauchy theorem, inverse VII.IB VII.1C IX.1C
Cauchy — Read theorem V.4A
CHARACTER I.3B
Character of a multiplicative mero-morphic function II.2D
Character of an l.m.m. II.2C
Character of an m-function VIII.4A IX.1A
Character, group I.3B
Choquet theorem II.4C
Circular set XI.6A
Cluster value theorem VI.7D VI.7E
Cocyle II.1A
Cohomology group II.1A
Convex function XI.1A
Corona problem X.5A
Cover transformation III.6B
Cover transformation, group of III.6B
Covering map III.6A
Covering triple III.6A
Critical point V.1C
Differential 1.7A
Differential, analytic 1.8A
Differential, conjugate I.7A
Differential, harmonic I.8A
Differential, reproducing (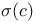 ) I.9B ) I.9B
Differential, with singularity 1.9A
Dirichlet problem I.5A III.3A VI.1B
Divisor I.10B
END VI.5A
Exhaustion I.1A
Exhaustion, canonical I.1C
Exhaustion, regular I.1A
Fatou theorem A.1.2
Fine boundary function III.4B
Fine limit III.4B
Function, balayaged I.6E
Function, boundary m VIII.4A
Function, convex XI.1A
Function, i IX.1A
Function, m VIII.4A IX.1A
Function, Martin III.IB
Function, Wiener III.5A
Fundamental group I.3A
Gelfand transform X.5A
Genus I.2B
Green function I.6A
Green function, modified V.7D
Green line VI.1A
Green lineconvergent VI.5A VI.5B
Green lineregular VI.1A
Green measure VI.1A
Green star region VI.1A
Hardy class IV.IB IV.3A
Hardy — Orlicz class XI.1A
Harmonic conjugate A.2.1
Harmonic differential I.8A
Harmonic measure I.5D III.2C
Harmonic, least, majorant 1.4C
Harmonic, minimal function III.2B
Harmonic, quasibounded function II.5A
Harmonic, singular function III.2C
Harmonizable III.5A
Hayashi theorem IX.1C IX.5D X.2B X.4A
Hejhal theorem XI.3B
Homology group I.2A
Hyperbolic region I.5C V.7A
Hyperbolically rare X.7B
| INNER II.5A
Inner, common factor II.5D
Inner, factor of an l.a.m. II.5D
Inner, greatest common factor II.5D
Inner, part II.5A
Integral representation III.2B
Invariant subspace VIII.1A VIII.2A
Invariant subspace, doubly VIII.1A VIII.2C
Invariant subspace, simply VIII.1A VIII.2C
Invariant subspace, theorem VIII.2C VIII.3B VIII.4C
Irregular boundary point I.5B
Kolmogorov theorem A.2.2
L.a.m. (locally analytic modulus) II. 2C
L.m.m. (locally meromorphic modulus) II.2C
L.m.m. (locally meromorphic modulus), inner II.5D
L.m.m. (locally meromorphic modulus), of bounded characteristic II.5D
L.m.m. (locally meromorphic modulus), quasibounded II.5D
LHM (least harmonic majorant) I.4C
Line bundle (bundle) II.2A
Martin boundary III.1B
Martin compactification III.1B
Martin function III.1B
Martin function, pole of a III.1B
Maximal ideal space X.5A
Mean value theorem IX.2D
Minimal point II.4C III.2B
Modulus of a section II.2A
Multiplicative meromorphic function II.2D
Multiplicative meromorphic function, inner factor of II.5D
Multiplicative meromorphic function, of bounded characteristic II.5D
Multiplicative meromorphic function, outer factor of II.5D
Nakai theorem X.8A X.8C
Normal operator V.6B
Null set XI.1A
Origin II.2B
Orthogonal decomposition II.5A
Outer character IX.1A
P-Outer character IX.1A
Parreau theorem VI.4A VI.4B XI.2B XI.2C XI.2D
Partition, identity V .6A
Partition, of the ideal boundary V.6A
Poisson kernel IV.1A A.1.2
Polar set I.6C
Potential I.6B
Pranger theorem X.6A
Principal branch II.2D
Principal operator V.6D
PWS (surface of Parreau — Widom Type) V.1A
Quasi-everywhere (q.e.) I.6C
Quasibounded II.5A IV.1C
Quasibounded, part II.5A
Radial limit VI.4A
Region (subregion) I.1A
Region (subregion), canonical I.1C
Region (subregion), curvilinear Stolz VI.3D
Region (subregion), Green star VI.1A
Region (subregion), hyperbolic I.5C V.7A
Region (subregion), regular I.1A
Region (subregion), Stolz VI.3D VI.7B A.1.2
Regular boundary point I.5B
Regularization V.3B
Riemann surface, of Myrberg type X.1A
Riemann surface, of Parreau — Widom type V.1A
Riemann surface, regular V.1C
Riemann — Roch theorem I.10C
Riesz theorem I.6F III.3B
Riesz theorem, F. and M . A.3.2
Section II.2A
Section, holomorphic II.2A V.2A
Section, meromorphic II.2A
Section, meromorphic-differential II.2E V.4B
Segawa theorem XI.7B
Singularity I.9A
Standard IX.1A
Stanton theorem X.1A X.5B
Stolz region VI.3D VI.7B A.1.2
Subharmonic function I.4A
Subregion, region
Superharmonic function I.4A
Support VIII.1A
Thin III.4A
Universal covering surface III.6A
Weak topology IV.5A
Weak-star maximality VII.6A
Widom theorem V.2B V.4C V.5C V.9A V.9B
Wiener function III.5A
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



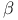 -dual
-dual 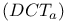
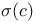 )
)