Авторизация
Поиск по указателям
Halmos P.R. — Measure Theory
Обсудите книгу на научном форуме Нашли опечатку?
Название: Measure TheoryАвтор: Halmos P.R. Аннотация: Useful both as a text for students and as a source of reference for the more advanced mathematician, this book presents a unified treatment of that part of measure theory which is most useful for its application in modern analysis. Topics studied include sets and classes, measures and outer measures, measurable functions, integration, general set functions, product spaces, transformations, probability, locally compact spaces, Haar measure and measure and topology in groups. The text is suitable for the beginning graduate student as well as the advanced undergraduate.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1974Количество страниц: 324Добавлена в каталог: 30.06.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
44 48 31 28 4 4 31 183 24 Absolute continuity 124 Absolute continuity for functions of a real variable 181 Absolute continuity for set functions 97 Absolutely normal numbers 206 Additive set functions 30 Additive set functions on semirings 31 Algebra of sets 21 Almost everywhere 86 Almost uniform convergence 89 Approximation of sets in a 56 Associated measure ring 167 Associated metric space 168 atom 168 Average theorem 261 Baire, contraction of a Borel measure 229 Baire, functions 223 Baire, measurable functions on a locally compact space 220 Baire, measure 223 Baire, sets 220 Base 3 Base at e 7 Bayes’ Theorem 195 Bernoulli’s theorem 201 Boolean 166 Boolean 166 Boolean algebra 166 Boolean algebra of sets 21 Boolean ring 22 165 Boolean ring of sets 19 Borel — Cantelli lemma 201 Borel, measurable functions on a locally compact space 219 Borel, measurable functions on the real line 78 Borel, measure 223 Borel, sets of a locally compact space 219 Borel, sets of n-dimensional Euclidean space 153 Borel, sets of the real line 62 Bounded convergence theorem 110 Bounded linear functional on 249 Bounded linear functional on 178 Bounded sets in locally compact spaces 4 Bounded sets in topological groups 7 Bounded variation 123 Cantor, function 83 Cantor, set 67 Cartesian product of measurable spaces 140 Cartesian product of measure spaces 145 152 157 Cartesian product of non 145 Cartesian product of sets 137 150 Cartesian product of topological spaces 4 Cavalieri’s principle 149 Center 5 Characteristic function 15 class 10 Closed sets 3 Closure 3 Coefficient of correlation 196 Collection 10 Compact sets 4 Complement 16 Complete Boolean ring 169 Complete measure 31 Completely regular spaces 5 Completion of a measure 55 Completion of a topological group 8 Completion, regular measure 230 Complex measure 120 Conditional expectation 209 Conditional probability 195 207 Conditional probability as a measure 210 Content 231 Continuity and additivity of infinite valued set functions 40 Continuity and additivity of set functions on rings 39 Continuity and additivity of set functions on semirings 40 Continuity from above and below 39 Continuous transformations 5 Convergence in measure 91 Convergence in the mean 103 Convergence of a series of sets 19 Convergence of sequences of measures 170 Convergence, a.e. 86 Convergence, a.e. and in measure 89 90 Convex metric spaces 169 Convolution 269 Coset 6 Countably, additive 30 Countably, subadditive 41 Cylinder 29 155 Decreasing of sets 16 Decreasing sequences of partitions 171 Dense, sequences of partitions 171 Dense, sets 3 Density theorem 268 Derivatives of set functions 133 Difference of two sets 17 Difference, set 68 DIMENSION 152 Discontinuity from above of regular outer measures 53 Discrete topological space 3 Disjoint 15 Disjoint, sequences of sets 38 Distance between integrable functions 98 Distribution function 80 Domain 161 Double integral 146 Egoroff’s theorem 88 Egoroff’s theorem on a set of infinite measure 90 Elementary function 86 Empty set 10 Entire space 9 Equal sets 10 Equicontinuous 108 Equivalent sequences of functions 201 Equivalent signed measures 126 Essential supremum 86 Essentially bounded functions 86 Exhaustion 76 Extended real number 2 Extension of measures 54 Extension of measures to larger 71 Fatou’s Lemma 113 Finite and totally finite measure spaces 73 Finite intersection property 4 Finite measure 31 Finitely additive 30 Finitely subadditive 41 Fubini’s Theorem 148 Full sets 52 132 Full subgroups 250 Fundamental in measure 91 Fundamental in the mean 99 Fundamental sequence 87 Generated 24 Generated hereditary class 41 Generated invariant 283 Generated monotone class 27 Generated ring 22 Graph 143 Group 6 Haar measure 251 Hahn decomposition 121 Hamel basis 277 Hausdorff measure 53 Hausdorff space 4 Hereditary class 41 Holder’s Inequality 175 Homeomorphism 5 Homomorphism 6 Horizontal line 131 Identity 6 Image 161 Increasing sequence of sets 16 Indefinite integral 97 Independent functions 192 Independent sets 191 Induced Borel measure 234 Induced inner content 232 Induced measure 47 Induced outer measure 42 233 Inequivalence of two definitions of absolute continuity 128 inf 12 Inferior limit 16 Infimum 1 Inner content 232 Inner measure 58 Inner regular content 239 Inner regular set 224 Integrable functions 102 Integrable simple functions 95 integral 95 102 Integration by parts 269 Interior 3 Intersection 13 INTO 161 Invariant 283 Invariant sets 29 Invariant subgroups 6 Inverse 6 Inverse image 76 161 Isomorphism 167 Iterated integral 146 J-cylinder 155 Jacobian 164 Join 14 Jordan decomposition 123 Kolmogoroff’s inequality 196 Lattice of sets 25 Lebesgue decomposition 134 Lebesgue integral 106 Lebesgue measurable function 78 Lebesgue measurable set 62 Lebesgue measure 62 153 Lebesgue — Stieltjes measure 67 Left Haar measure 252 Left invariance 252 Left translation 6 Lim inf, limit, lim sup 16 Linear functional on 243 Linear functional on 178 Linearly independent sets 277 Locally bounded 8 Locally compact 4 Lower, ordinate set 142 Lower, variation 122 Lusin’s theorem 243 Mean convergence 103 Mean fundamental 99 Mean value theorem 114 Measurability preserving transformation 164 Measurable cover 50 Measurable function 77 Measurable function of a measurable function 83 Measurable group 257 Measurable kernel 59 Measurable rectangle 140 154 Measurable set 73 Measurable set which is not a Borel set 67 83 Measurable space 73 Measurable transformation 162 Measure 30 Measure in metric spaces 40 Measure on intervals 35 Measure, algebra 167 Measure, preserving transformation 164 Measure, ring 167 Measure, space 73 Meet 14 Metric outer measures 48 Metric spaces 5 Minkowski’s inequality 176 MODULO 127 Monotone class 27 Monotone class generated by a ring 27 Monotone functions of a real variable 179 Monotone sequences 16 Monotone set functions 37 Multiplication theorem 195 Mutually singular 126 Negative part 82 Negative sets 120 Neighborhood 3 Non atomic 168 Non coincidence of complete 58 Non measurable sets 69 Non product measures in product spaces 214 Non regular measures 231 Non regular outer measures 52 53 72 Non term by term integrability 111 112 Non uniqueness of extension 57 Norm 171 Normal class 28 Normal numbers 206 Normalized 171 One to one 161 One to one measurable transformation which is not measurability preserving 165 One-point compactification 4 Onto 161 Open covering 4 Open set 3 Open transformation 5 Outer measure 42 Outer measures on metric spaces 48 Outer regular sets 224 Partition 31 47 171 Point 9 Point at infinity 240 Positive linear functional 243 Positive measure 166 Positive part 82 Positive sets 120 Principle of duality 17 Probability measures and spaces 191 Product measures 145 Product of a sequence of measures 157 Product of partitions 32 48 Product of transformations 161 Projection 6 Proper difference 17 Purely atomic 182 Quotient group 6 Rademacher functions 195 RADIUS 5 Radon — Nikodym theorem 128 Radon — Nikodym theorem, counter examples to generalizations 131 RANGE 161 rectangle 137 150 154 Regular contents 237 Regular measures 224 Regular outer measures 52 Regular sets 224 Relative complement 17 Relative topology 3
Реклама
 |
|
О проекте
|
|
О проекте



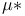 -measurable sets
-measurable sets  -partition
-partition  -algebra
-algebra