|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Burn R.P. — Numbers and Functions: Steps to Analysis |
|
|
 |
| Предметный указатель |
Logarithmic function 1.8 App.
Logarithmic function as limit 4.41 10.6
Logarithmic function as series 5.65 5.106 9.41—9.42 11.38
Logarithmic function, additive property 4.41 10.9
Logarithmic function, defined 11.22 11.25 11.30
Lower bound 3.5 4.67—4.70
Lower sum 10.16
Maclaurin 5H 9.37 9H
Mapping 6.1; see “function”
Maurolycus 1H
Maximum, local 8.29—8.32 9.2
Maximum, Of two real functions 6.45
Maximum, of two real numbers 6.44
Maximum-minimum Theorem 7.31—7.32 7.34 7H
Mean value theorem 9.13 9H
Mean Value Theorem for Integrals 10.45 10.59
Mean Value Theorem, nth 9.35
Mean Value Theorem, second 9.31 9H
Mean Value Theorem, third 9.33 9H
Mengoli 5H
Meray 4H
Mercator 11H
Mertens 3H
Monotonic functions 7.1—7.2
Monotonic functions, integrability of 10.7—10.8
Monotonic functions, one-sided limits of 7.5—7.7
Monotonic sequences 3.4 3.11 3.16 3.79 3.80 4.33—4.35
Napier 11H
Natural numbers 1.1 1.8
Neighbourhood 3.61 6.56—6.72
Neighbourhood, continuity by 6.64—6.72
Neighbourhood, limit by 6.83—6.85 6.87
Nested intervals 4.32 4.42
Newton 3H 4.37 5H 8H 9H 10.7 11H 12H
Newton — Raphson App. 3.24
Nth roots 2.20 2.50—2.51 3.56—3.59 4.40—4.41 7.19 7.27 App.
Null sequences 3.24—3.47
Null sequences, absolute value rule 3.33
Null sequences, definition 3.28
Null sequences, difference rule 3.46
Null sequences, product rule 3.43
Null sequences, scalar rule 3.32
Null sequences, shift rule 3.36
Null sequences, squeeze rule 3.34 3.36 3.46
Null sequences, sum rule 3.44
Null sequences, test for divergence of series 5.11 5H
Open interval 3.78 7.9
Order 1H 2.1—2.29
Oresme 5.10 5H
Partial fractions 5.3
Partial sums of series 5.5 5.22
Pascal 1H
Pascal's triangle 1.4
Pasch 4H
Peacock 2H
Peano 1H 3H
Peano postulates 1H
Pointwise limit function 12.5
Polya 5.27
Positive 2.1 App.
Positive squares 2.15
Power series, circle of convergence 5.94
Power series, convergence 5.78—5.107 9.42 12.36—12.38
Power series, radius of convergence 5.94 5.102
Principle of Completeness 5.31 App.
Pringsheim App. 3.19
Property of Archimedean Order 3.18 3.29 App.
Quadling 11.1
Radius of convergence 5.94 5.102 5H 12.40—12.42
Range of function 6.1
Rearrangement of scries when absolutely convergent 5.76—5.77
Rearrangement of scries when conditionally convergent 5.72—5.75
Repealed bisection 4.40 4.53 4.80 7.12
reverse 2.63
Riemann 5.75 5H 6H 7H 8H 10.23—10.24 10H
Rolle's theorem 9.1—9.8 9H
Ruler function 6.72 10.36
Sandwich theorem see “squeeze rule”
Scalar rule 3.32 3.54 5.19
Schwarz 9H
Second comparison lest 5.53
Second comparison lest, limit form 5.55
| Seidel 12H
Sequence of partial sums 5.5
Sequence, bounded 3.5 3.13—3.14 3.62
Sequence, constant 3.3 3.28 3.38 3.50
Sequence, convergent 3.48—4.83
Sequence, decreasing 3.4
Sequence, graph of 3.2
Sequence, increasing 3.4
Sequence, monotonic 3.4 3.80 4.33—4.35
Sequence, null 3.24—3.47
Sequence, tends to infinity 3.18 3.20—3.23 3.31
Series of positive terms 5.23—5.61 5.76
Series, convergent 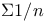 5.27—5.32 5H 5.27—5.32 5H
Series, convergent absolutely 5.67
Series, convergent by alternating series test 5.63
Series, convergent by Cauchy's nth root test 5.35 5.38 5.70
Series, convergent by d'Alembert's ratio test 5.43 5.47 5.68—5.69
Series, convergent by first comparison test 5.26
Series, convergent by integral test 5.57 5H
Series, convergent by second comparison test 5.53 5.55
Series, convergent conditionally 5.71
Series, divergent 5.10 5.11 5.28—5.30
Series, harmonic 5.30
Series, Maclaurin 9.37—9.43
Series, rearrangement of 5.72—5.77 5H
Series, Taylor 9.35—9.46
Shift 3.13
Sine defined 9.39 11.51—11.58
Spivak 8.22 11.39
Square roots 2.17
Square roots, irrational 4.18—4.20
Square roots, real 4.37 4.39
Squares positive 2.15
Squeeze rule for continuous functions 6.36
Squeeze rule for convergent sequences 3.54
Squeeze rule for limits 6.98
Squeeze rule for null sequences 3.34 3.36
Start rule for scries 5.16
Step function 10.12—10.15
Step function, lower 10.16
Step function, upper 10.18
Subsequence 3.8—3.16
Subsequence of null sequence 3.36
Subsequence, convergent 4.43—4.46
Subsequence, monotonic 3.11 3.15—3.16
Sum rule 3.44 3.54 5.21 6.23 8.10
Sum, lower 10.16
Sum, upper 10.18
Supremum 4.62—4.66 4.80 4.82—4.84 7.5 7.7 9.4 10.16 10.21 12.12—12.15;
Surjection 6.2
Tagaki 8.22
Tall 8.22 App.
Tangent function defined 11.59—11.62
tangents 8.1—8.4
Taylor's theorem 8H 9H
Taylor's Theorem with Cauchy's remainder 9.45—9.46 10.59
Taylor's Theorem with Lagrange's remainder 9.35 9.42
Taylor's Theorem, integral form of remainder 10.59 10H
Thomae 6.72 10.36 10H 11H
Torricelli 10H
Transitive law, for order 2.9
Triangle inequality 2.61—2.62 2.64
Trichotomy law. for order 2.1 2.7 App.
Trigonometric functions 11.39—11.62 App.
Unbounded 3.5
Uniform continuity 7.37—7.44
Uniform convergence 12.15
Uniform convergence of power series 12.35—12.42
Uniform convergence, continuity 12.20—12.23
Uniform convergence, differentiability 12.32—12.34
Uniform convergence, integrability 12.24—12.31
Upper bound 3.5 4.59—4.61
Upper sum 10.18
Variable 6.1
Variable, real 6.1
Veronese 3H
Volterra 10.52
Wallis 1H 3H 11H
Waring 5H
Weierstrass 2H 3H 4H 6H 7.34 7H 8.21 8H 9H 11H 12H App.
Weierstrass M-test 12.36
Well-ordering principle 11H
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте