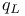Reid M., Szendroi B. — Geometry and Topology :: Электронная библиотека попечительского совета мехмата МГУ

Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск Форум

Авторизация

Поиск по указателям

Reid M., Szendroi B. — Geometry and Topology

Обсудите книгу на научном форуме

Нашли опечатку?
Выделите ее мышкой и нажмите Ctrl+Enter

Название: Geometry and Topology

Авторы: Reid M., Szendroi B.

Аннотация:

An introduction to the ideas of geometry and includes generous helpings of simple explanations and examples.

Язык:

Рубрика: Математика/

Статус предметного указателя: Готов указатель с номерами страниц

ed2k: ed2k stats

Год издания: 2005

Количество страниц: 240

Добавлена в каталог: 11.06.2008

Операции: Положить на полку | Скопировать ссылку для форума | Скопировать ID

Предметный указатель

Abstract group      169
Affine frame      69 71
Affine geometry      62—72 95
Affine group Aff(n)      102 161 170
Affine linear dependence      68 71
Affine linear map      8—9 27 68—69
Affine linear subspace      29—30 62—68 70—72 91
Affine space $\mathbb{A}^n$       62 63 68 95 170
Affine space $\mathbb{A}^n$ in projective space      82
Affine span      62 66—67
Affine transformation      xvi 8—9 68—70 91
Algebraic topology      xv 113 130
Algebraically closed field      136—137
angle      1 5—6 27 62 69 95
Angle bisector      23 25
Angle of rotation      15—18
Angle sum      19—20 34 40 51—56
Angle, signed      6
Angular defect, excess      see angle sum
Area      40—41 51—56
Associative law      28 32 94 169
Axiomatic projective geometry      86—88 164 168 177
Ball      58 109 138 146
Based loop      131—133 136—137
Basis for a topology      124—126
Bilinear form      see Euclidean inner product Lorentz 162 183—185
Bolyai's letter      166
Centre of rotation      15
Centroid      21 69—71
Circumcentre      21 22
Closed      see compact versus closed 58 75 108 111 113 138 148
Closed and bounded      115—129 146
Closed map      129—130
Closed, diagonal      127—128
Cofinite topology      108 111 127
Commutative law      15 17 28 32
Compact      see maximal compact sequentially xv 75 115—117 121 133—138 143 146 152
Compact Lie group      146 147 160
Compact surface      119 177—178
Compact versus closed      128—129
Compactification      75
Complex number      12 27 136 188
Composite of maps      26—33
Composite of reflections      16 29—31 33 58
Composite of rotation and glide      33
Composite of rotation and reflection      31
Composite of rotations      27 33
Composite of translations      27
Congruent triangles      19 25 55
Connected      see path connected simply 113—115 117 138 148 149 152 153
Connected component      114—115 122 144 148 149 153 160 161
Connected Lie group      160
continuous      xv 5 68 91 100 142—144 148 149
Continuous, family of paths      131—132
Contractible loop      130—133 136 141
Coordinate changes      xiv
Coordinate frame      xiv 1
Coordinate geometry      xiii xvi 168
Coordinate system      xiv 4
Coventry market      92—93
Cross-ratio      79—81 90 106
Curvature      34 40 49 93 167 177 178 182
Desargues' theorem      82—84 88 90
DIMENSION      66 67 70 76 144 145 160
Dimension of a Lie group      144—146 148 161
Dimension of intersection      67 69 72—73 77 81 83 88
Direct motion      10 15 17 148 151—152
Disc      111 122 130 133 139
Discrete topology      108 110 127 143
Distance      see Euclidean distance hyperbolic metric shortest spherical
Distance function      1 2 4 6 7 35 62 95 180 181 183
Duality      85—86 90
Einstein's, field equations      see general relativity 93
Einstein's, relativity principle      see special relativity 174
Electron      xvi 143 154—159 175
Empty set      68 70 72 73 76 108 124
Erlangen program      xiv—xv 95—96 112 170—171
Euclid's postulates      see parallel postulate 165—167
Euclidean angle      45
Euclidean distance      1 2 4 116 151
Euclidean frame      1 14 25 40 145
Euclidean geometry      4 19 25 34 45 47 69 95 166
Euclidean group Eucl(n)      xvi 159 161
Euclidean inner product      2 5 9 24 43 58 184 185 187
Euclidean line      4
Euclidean motion      see motion 9 10 14 24 25 47 92 144
Euclidean plane $\mathbb{E}^2$       6 33
Euclidean space $\mathbb{E}^n$       1 4—10 29 35 180
Euclidean translation      19
Euler number      140 177
Family of paths      131
Feuerbach circle      23
Frame      see affine frame coordinate Euclidean orthogonal projective spherical
Frame of reference      see projective frame
Fundamental group      xv 113 130 159
Fundamental theorem of algebra      136
Galilean group      93 172—173
General linear group GL(n)      xv 95 99 101 105 124 143 145 147 148 160 161 171
General relativity      93 167 176 178
Generators      29 100—101 103 106
Genus      120 139 177
Geodesic      see shortest distance
Glide      15—17 24 31—33 40 47 98
Glide reflection      see glide
Glueing      see quotient topology
Great circle      see spherical line
Group      see abstract group fundamental Galilean general Lie Lorentz Poincare projective reflection rotation spinor topological transformation unitary
Half-turn      12 32
Hausdorff      109 110 127—130 139 152
Heine — Borel theorem      116
Hermitian form      153 156 160 163 188
Homeomorphism      107 111 113 117 119—121 130 132 134—136 138 139 147 149 152 153 160 177
Homeomorphism criterion      111 130 142 152
Homeomorphism problem      xv 113
Homogeneous space      169—170
Hyperbolic distance      43 46 58
Hyperbolic geometry      4 20 34 36 41—167
Hyperbolic line      43 46—50 60
Hyperbolic motion      46 144
Hyperbolic plane $\mathcal{H}^2$       39 47—49 58—61 180
Hyperbolic sine rule      59
Hyperbolic space      35 42 51 104
Hyperbolic translation      47 58 61
Hyperbolic triangle      44 51 58 59
Hyperbolic trig      35 44—45
Hyperplane      29 30 66 67 76 78 81 82 89 96
Hyperplane at infinity      88
Ideal point      see infinity point
Ideal triangle      51 53—56
Incentre      23 25
Incidence of lines      34 40 47 69 84
Indiscrete topology      108 111 139
Infinity, hyperplane at      72 73 76 82 90
Infinity, point at      48—49 51 53 55 59 73 75 76 79
Intersection      see dimension of intersection 108
Intrinsic curvature      34 40 177
Intrinsic distance      40

Intrinsic unit      34 49
Isometry      see motion preserves 4 6 112 181
Klein bottle      xiv 139
Length of path      5
Lie group      see compact Lie group 142—164 169
Line      4 65
Line, hyperbolic      44
Line, segment      3 65
Line, spherical      35
Loop      107—137 140 159
Lorentz basis      44 55 185 186 188 189
Lorentz complement      48 186
Lorentz dot product $\cdot_L$       43 184 186
Lorentz form       42 47 184 186 189
Lorentz group      93 159 161
Lorentz matrix      42 46—47 161 188 189
Lorentz norm      44 184 186
Lorentz orthogonal matrix      187
Lorentz reflection      47
Lorentz space      42 46 188
Lorentz transformation      47 54 92 144
Lorentz translation      see hyperbolic Lorentz
Lorentz, orthogonal      44
Lorentz, pseudometric      42 58 174
Maximal compact subgroup      160
Mercator's projection      139 164 179
Metric      180—182
Metric geometry      64 177
Metric space      1 4 38 180—182
Metric topology      109 125 143 152
Minimum over paths      5 180
Moebius strip      xiv 107 118—119 122 139
Motion      xiv 1 6 7 9—11 14—19 24—26 28—34 38—40 46 47 58 61 93 95 97 98 100 103 105 106 144 149 151 152 154 158 161
Mousetrap topology      122—123
Musee Grevin      103 105
Newtonian dynamics      93 161 172—173
Non-Euclidean geometry      34—61 167
Normal form of a matrix      10—13 18 29 98—99 148 189
Open set      108—111 113—115 117 118 121 125 143 148
Opposite motion      10 15 17 148
Orthocentre      22—23
Orthogonal      see Lorentz -
Orthogonal axes      1
Orthogonal complement $V^{\perp}$       13 47 145 171 185
Orthogonal direct sum      151
Orthogonal frame      39
Orthogonal group O(n)      144—152
Orthogonal line      158
Orthogonal magnetic field      154 158
Orthogonal matrix      7 9—13 24 29 39 99 144 146—149 159 187
Orthogonal plane      29
Orthogonal transformation      9 92 99 187
Orthogonal vector      5 29 37 151 162 185
Pappus' theorem      84—85 88 90
Parallel axes      31
Parallel hyperplanes      17 64 66 67
Parallel lines      15—17 20—23 27 34 40 49 62 68 70 73 82 166
Parallel mirrors      103
Parallel postulate      20 49 60 166
Parallel sides      31
Parallel vector      16 96
Path      see length of path minimum 114 131 159
Path, connected      114 120 132 141 149
Perpendicular bisector      16 21 22 24 29 30 57
Perspective      73 74 81—83 88 90
Physics      xv xvi 93 160 172—179
Poincare group      173—176
Point at infinity      see infinity point
Preserves distances      6—7 24 39 181
Principal homogeneous space      see torsor
Pringle's potato chip      58 178
Product topology      126—127 139 143
Profinite topology      125 126
Projective frame      78 79 90 106 146
Projective geometry      72—91
Projective linear group PGL(n)      77 95 105 106 144 146 171
Projective linear subspace      73—77
Punctured disc D*      120 130 133 136
Quadratic form      5 9 42 123 150 151 183
Quaternions      149—152
Quotient topology      110 117—119 121—125 139—140 144 152
Reflection      1 11 15—17 24 27—30 33 34 40 58 103 105
Reflection group      103—105
Reflection matrix      7 10 24 42 144
Relativity      see special relativity general 161
Rigid body motion      see motion
Rotary reflection      33 40
Rotation      1 11 15—18 24 25 27 29 31—34 39 40 47 97 100 103 142 143 149—152 154 158 161
Rotation group      152
Rotation matrix      7 10 42 144
Rubber-sheet geometry      xiv 107
Sequentially compact      115—116 138
Shortest distance      see minimum over paths 4 5 40 46 58
Similar triangles      21—23
Simplex of reference      see projective frame
Simply connected      130 132 146 160
Spacetime      93 172—176 178 179
Special linear group SL(n)      159 175
Special orthogonal group SO(n)      149 152
Special relativity      xv 93 144 173—174 178
Special unitary group SU(n)      153 176
Sphere       35 36 39 40 43 56 58 113 180 181
Sphere       57 58 116 121 122 145 151
Spherical disc      56
Spherical distance      36—38 40 56 116
Spherical frame      34 40
Spherical geometry      4 20 34—41 45 56 57 164 167 182
Spherical line      39 40
Spherical motion      38 39
Spherical triangle      37—38 40 41 57 182
Spherical trig      37 167
Spin      143 154 155
Spinor group Spin(n)      153 159
Standard model      176
Subspace topology      117 121 128 144 147 152
Symmetry      92—95 160 164 169 173—176
Topological group      143—144 159
Topological property      xv 113 127 131 136 167
topology      94 107—141 143
Topology of       152
Topology of $\mathbb{P}^n$       90 121 139
Topology of SO(3)      142 143 149
Torsor      169–170
Torus      119 120 139 177 178
Transformation group      26—33 92 94—96 101 104 112 142—163
Translation      1 15—19 25 29 31—33 39 68 97 98 100—103 106 158 161
Translation map      125
Translation subgroup      101 105
Translation vector      15 24 27 31
Triangle inequality      1—5 38 45 180
Trichotomy      177—179
Ultraparallel lines      48—51 59 61
UMP      see universal mapping property
Unitary group      153 176
Unitary matrix      153 158 188—189
Unitary representation      175
Universal mapping property      118 139 152
Winding number      xv 107 130—137

О проекте