|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Brown K.S. — Cohomology of Groups |
|
|
 |
| Предметный указатель |
 -functor 78 -functor 78
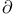 -functor 75 -functor 75
Abelianization 36
Abeliar groups (calculation of homology of) 121ff
Abutment 163
Acyclic chain complex 5
Acyclic chain complex, contractibility of 24 30 132 274
Acyclic cover 168 265
Acyclic models theorem 25
Acyclic module (with respect to a homology theory) 72
Acyclic space 15
Additive category 25
Additive functor 33
Admissible  -complex 258 -complex 258
Admissible acyclic chain complex 129
Admissible exact sequence 129
Admissible injection 129
Admissible product 118
Alexander — Whitney map 108 286
Amalgamation (or amalgamated free product) 49ff
Amalgamation (or amalgamated free product), tree associated to 53
Anti-commutati vity 111 118
Arithmetic groups 217 218
Arithmetic groups, Euler characteristic of 254ff
Aspherical space 1 15
Associated graded module 162
Augmentation ideal and map 12
Augmentation-preserving chain map 23 132
Automorphism group 102
Automorphism group, outer 104
Bar resolution 19
Bernoulli numbers 255
Binary icosahedral group 47 155
Binary octahedral group 155
Binary tetrahedral group 155
Boundaries 4
Boundary operator 4
Cap product 112—113 141
Cartan — Leray spectral sequence 173
Chain complex 4
Chain map 5
Chevalley group 254
Co-compact 217
Co-effaceable 73
Co-extension of scalars 63
Co-free module 66
Co-induced module 67
Co-invariants 34
Coboundaries 4
Cocycles 4
Coefficient system 167
Cohomological dimension 184
Cohomological dimension, virtual 226
Cohomological functor 78
Cohomologically trivial module 148 287
Cohomology of a cochain complex 4
Cohomology of a group 57 134 170 277
Cohomology of a group, equivariant 172 180ff 281ff
Cohomology with compact supports 209
Combinatorial path 42
Commutator pairing 97
Compact supports 209
Complete diagonal approximation 138 275
Complete resolution 132 273
Complete tensor product 137
Composition product 115 143
Congruence subgroup 40
Conjugation action 48 79 80
Connecting homomorphism 6 71 75
Connecting homomorphism, interpretation in terms of group extensions 95
Contractible, contracting homotopy 5 (see also “Acyclic chain complex”)
Convergence of a spectral sequence 163
Corestriction map 80 136
Cross product 109
Crossed homomorphism 45 88
Crossed module 102
Cup product 109 130ff 278
Cup product in cyclic groups 114
Cycles 4
Cyclic group (resolution, homology, etc.) 16 21 35 58 114
Deck transformation 31
Degree 4
Derivation 45 88
Derivation, principal 60 89
Diagonal action 55 56
Diagonal approximation (or map) 108 138 275 286
Differential 4
Dihedral group 98
Dimension, Cohomological 184
Dimension, geometric 185 205
Dimension, homological 204
Dimension, projective 152 184 287
Dimension, virtual cohomological 226
Dimension-shifting 74 136
Direct limits and homology 121 195
Discrete subgroups of Lie groups 38ff 217ff
Divided polynomial algebra 119 125
Divided powers 124
Divisible module 66
Double complex 164
Double coset formula 69 82
Dual 28 133 145
Duality group 221
Duality group, Poincare 222
Duality group, virtual 229
Duality pairing 145
Duality theorem 28 144ff
Dualizing module 221 276
Effaceable 72
Eilenberg trick 187—188
Eilenberg — Ganea theorem 205
Eilenberg — MacLane complex (or space) 15 40
Eilenberg — MacLane complex (or space), existence of 18 19 205
Elementary abelian p-group 156 267 271
ends 223
Equivariant Euler characteristic 249—250
Equivariant homology and cohomology 172 180ff 281ff
Euler characteristic 164 243ff
Euler characteristic of a group 247 249
Evaluation maps and pairings 9 113 145 234
Exact functor 8
Ext 60
Extension (group) 47 86ff 171 248 257 281
Extension of scalars 62
Exterior algebra, exterior power 97 119 121
F-isomorphism 286
Factor set 91
Farrell cohomology 277ff
Filtration 162
Finite chain complex, resolution 243
Finite homological type 246
Finitely dominated space 200
Finitely presented module 193
Finiteness conditions 184ff
Finiteness conditions, FL 199
Finiteness conditions, FP, 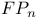 , , 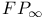 193 195 197 193 195 197
Finiteness conditions, VFL 226
Finiteness conditions, VFP 226
Finiteness conditions, WFL 226
Five-term exact sequence 47 171 175
Fixed-point theorems 21 181 246 261
Fixed-point-free representation 154
Flat module 29 56
Free derivative 45 90
Free G-set, G-complex 13
Free group (homology, resolution, etc.) 16—17 37 247
Function complex 5
Fundamental class 145 204
| Fundamental group of a graph of groups 179
Fundamental lemma of homological algebra 22 130
G-complex (or G-CW-complex) 14
G-module 13
G-set 13
Gauss — Bonnet measure 253
General linear group 38
Generalized quaternion group 98 155
Geometric dimension 185 205
Gottlieb’s theorem 252
Graded module 4
Graph 52
Graph of groups 179
Group extension 47 86ff 171 248 257 281
Group ring (or algebra) 12 14
Hatton — Stallings rank 233
Hirsch number 186
HNN extension 179
Hochschild — Serre spectral sequence 171 281
Homological dimension 204
Homological functor 75
Homology of a chain complex 4
Homology of a group 1 35 56 135 168 172
Homology of a group, equivariant 172 180ff 281
Homotopy, homotopy equivalence 5ff 29
Hopf’s theorems 1 41
Hopf’s theorems, explicit formula for 46
Horn 56
Idempotent 27 234 238
Induced module 60 67ff
Injective module 26 65ff
Invariant cohomology class 84
Invariants 27
Invertible ideal 27
Irdecomposable 231 235 236
K(G, l)-complex 15 (see also “Eilenberg — MacLane complex”)
Knol groups 212
Krull dimension of H*(G) 159
Kummer’s criterion 270
Kunneth formula 7 109 120
Lefschetz fixed-point theorem 21 246 261
Length of a resolution 11
Lie groups (discrete subgroups of) 38ff 217ff
Long exact homology sequence 6 71 75
Lyndon’s theorem 37 44 185 228
Mapping cone 6
Mayer — Vietoris sequence 51 74 178ff
Nakayama’s Lemma 150 236
Nerve of a covering 166
Nilpotent group (cohomological dimension of) 186 213
Norm element 20 58
Norm map 58
Normalized bar resolution 19
One-relator group 37 44 185 228
Ordered simplicial complex 227
Outer automorphism group 104
p-groups with a cyclic subgroup of index p 97ff
p-groups with a unique subgroup of order p 99
p-groups with every abelian normal subgroup cyclic 101
p-groups, calculation of homology via 84
Partially ordered set (topological concepts applied to) 261 262 291
Perfect group 46 96 198
Periodic cohomology and resolution 20 133 153 158 180 288
Permutation module 13
Poincare duality group 222
Pontryagin product 117
Primary decomposition of homology groups 84 141
Principal derivation 60 89
Product, cap 112—113 141
Product, composition 115 143
Product, cross 109
Product, cup 109 130ff 278
Product, of ordered simplicial complexes 227
Product, shuffle 118
Product, tensor 7 10 55 107 137
Projective dimension 152 184 287
Projective module 21 26ff 56
Projective module over a group ring 27 149 152 201
Projective module over a local ring 235
Projective module, rank of 230ff
Projective module, stably free 201
Proper  -complex 226 -complex 226
Proper action 39
Pull-back 94
Quaternion group 98 155
Quillen’s theorem 159
Rank of a finitely generated abelian group 242
Rank of a nilpotent group 186
Rank of a projective module 230fF
Reduced homology 211
Regular cover 31
Regular cover, spectral sequence of 173
Relation module 43 44 90 198
Relative homological algebra 25.129ff
Relative injective module 129
Relative injective resolution 131
Representable factor 25
Resolution 10
Resolution, bar 19
Resolution, complete 132 273
Resolution, finite 199
Resolution, of finite type 193
Resolution, periodic 20 133 153
Resolution, standard 18
Resolution, uniqueness of 24
Resolution, via topology 14ff
Restriction map 80 136
Restriction of scalars 62 69
Rim’s theorem 152 287
Schanuel’s Lemma 192 193
Semi-direct product 87
Serre’s theorem 190
Shapiro’s Lemma 73 136
Shu file product 118
Simple module 149
Simplicial complex (ordered) 227
Simplicial complex (ordered), associated to a partially ordered set 261—262
Simplicial product 227
Solomon — Tits theorem 270
Spec A 235
Special linear group 39 157ff 213ff 229 255
Spectral sequence 162ff
Split extension 87
Stably free 201
Stallings — Swan theorem 185 223
Standard resolution 18
Strict anti-commutativity 118
Strict upper triangular group 38 185 213
Suspension 5
Swan’s theorem 240—241
Sylow subgroups (calculation of homology via) 84
Symmetric group 48 85 114
Symplectic group 255 269
Tate homology and cohomology 134ff 170 180ff
Tensor product 7 10 55 107 137
Tor 60
Trace 231—232
Transfer map 80 83ff
TREE 53
Type FL, FP, etc. see “Finiteness conditions”
Universal central extension 96
Universal coefficient theorem 8 127 170 198 202
Upper triangular group 38 185 213
Virtual notions 225fT
Weak equivalence 5ff 29
Yoneda’s Lemma 25
Zariski topology 236—237
Zeta function 254
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -functor
-functor 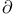 -functor
-functor  -complex
-complex 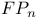 ,
,