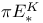|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Thomas C.B. — Elliptic Cohomolgy (The University Series in Mathematics) |
|
|
 |
| Предметный указатель |
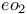 (Hopkins) 156 (Hopkins) 156
Abelian varieties 164
Abelian varieties, dimension 2 167
Abelian varieties, Jacobian 165
Abelian varieties, principally polarized 165
Atiyah invariant 149
Baas — Sullivan construction 27
Baas — Sullivan construction, manifolds with singularity 28
Brown — Peterson theory (BP) 26 87 100
Brown — Peterson theory (BP), 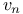 -periodicity 27 -periodicity 27
Burnside ring 44 81 116
Cayley numbers 147 160 183—185
Character ring 36
Character ring, elliptic 117
Characteristic class 8
Characteristic class, Chern 8 62
Characteristic class, generalized 25
Characteristic class, Pontrjagin 9
Characteristic class, Stiefel — Whitney 75
Characteristic class, transferred Euler 92
Characteristic number 9 151 179
Class functions 36
Class functions for pair  , , 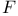 37 37
Class functions for pair  , , 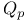 39 39
Cobordism ring 7 23 179
Cobordism ring, 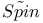 , ,  147 159 147 159
Cobordism ring, equivariant 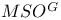 103 113 103 113
Cobordism ring, oriented  7 7
Cobordism ring, Spin,  23 147 23 147
Cohomology of BG 61
Cohomology of BG, Chem subring 62 89
Cohomology of BG, generalized 82
Cohomology of BG, invariant elements 63
Cohomology of BG, p-periodicity 64
Cohomology of BG, p-rank = 2 71 92
Cohomology of BG, spectral sequence of extension 65
Cohomology of BG, stable elements 63
Cohomology, complex oriented 25—26
Cohomology, elliptic 29
Cohomology, elliptic, level 1 100 144
Cohomology, elliptic, level 2 29
Cohomology, elliptic, level N (Baker) 144 146
Cohomology, elliptic, level N (Brylinski) 146
Cohomology, K3/string 159 170—171 176
Completion Theorem 36 110 115
Completion, I-adic 36 42 109 110
Completion, p-adic 36 109
Congruence subgroup 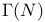 25 52 187 25 52 187
Contraction property (Segal) 122
Curvature, Ricci (positive) 162
Curvature, scalar (positive) 151 162
Discriminant  24 29 31 144 157 24 29 31 144 157
Elliptic curve, Jacobi 12 19 24
Elliptic curve, Weierstrass 24 31
Elliptic homology (Kreck — Stolz) at odd primes 147 151
Elliptic homology (Kreck — Stolz), 2-local 153
Elliptic object 123
Elliptic system (for finite group G) 126
Equivariant elliptic cohomology, 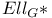 (Devoto) 103 (Devoto) 103
Euler characteristic (equivariant) 81—82
Exceptional Jordan algebra 184
Fermat hypersurface 173
Finite groups,  75 75
Finite groups, 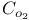 75 75
Finite groups, 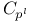 36 43 62 109 36 43 62 109
Finite groups, 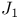 87 87
Finite groups, $p_+^{1+2} $64
Finite groups, 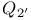 71 71
Finite groups, 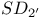 71 71
Finite groups,  61 87 61 87
Finite groups, M 75 141
Finite groups, Mathieu 49 see
Finite groups, order = 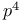 98 98
Finite groups, p-rank = 2 92 97
Flat bundles 35 62 134
Flat bundles, maps 35 42 107 116
Formal group 10 26
Formal group, coordinates 171
| Formal group, elliptic curve 24
Formal group, height 40
Formal group, K3-surface (Brauer) 171
Formal group, logarithm 10
Genus zero condition 130
Genus, 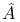 12 12
Genus, elliptic 12 161
Genus, L 12
Genus, Mathieu 56
Genus, Ochanine 149
Genus, strongly multiplicative (rigid) 14
Genus, Witten 161
Green functor, associated modules 81
Green functor, axioms 80
Green functor, Frobenius reciprocity 80
Gysin map 26
Hecke algebra 52
Human Capital and Mobility (HCM) 4
Igusa polynomial 109
Isom 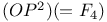 184 184
Johnson — Wilson theory E(n) 91 181
Kriz counterexample 99
Kummer varieties 168
Kummer varieties in dimension 2 169—170
Kummer varieties, defining equations 168 176—177
Kummer varieties, symplectic automorphism group 188
Landweber exactness condition 27 30 181
Loop space,  (double) 125 133 (double) 125 133
Loop space, LBG 123
Loop space, LX 131
Mackey functor, axioms 80
Mackey functor, double-coset formula 80
Mathieu groups,  49 74 49 74
Mathieu groups, 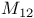 49 74 49 74
Mathieu groups, 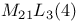 , , 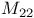 50 71—76 50 71—76
Mathieu groups, 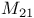 71—73 71—73
Mathieu groups, 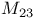 49 71—73 137 188 49 71—73 137 188
Mathieu groups, 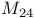 49 64 68 100 127 49 64 68 100 127
Mathieu groups, Coxeter representation 74
Mathieu groups, Steiner systems 49
Mathieu groups, Todd representation  51 68 51 68
Milnor manifolds 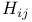 15 15
Mirror Symmetry 177
Modular forms 25 52 173
Modular forms, cusp 52
Modular forms, degree 174
Modular forms, eigenforms 54
Modular forms, generating families 25 144 175
Modular forms, invariance subgroup 52
Modular forms, level 52 56 143 146
Modular forms, topological 157
Modular forms, weight 52
Modular functions 130
Moonshine for 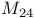 51 53 130—131 51 53 130—131
Moonshine for M 141—142
Moonshine, Norton condition 104 142
Morava K-theory K(n) 90 99 101 182
Multiplicative genus 9
Multiplicative sequence 10
Prize question (Hirzebruch) 158
Projective plane functors 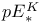 , , 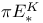 147 147
Quantum field theory 119—120
Quantum field theory, conformal 120
Quantum field theory, topological 119
Ramanujan numbers 58
Spectrum 100 153—156 180
Stable cohomotopy 81 116
Theorem, Adams 44
Theorem, Hopkins — Kuhn — Ravenel 42
Theorem, Landweber — Ravenel — Stong 29
Theorem, Lubin — Tate 40
Theorem, Taubes 15
Thompson series 53 55 58 130
Vector bundles with connection 123
Vector bundles, admissible (over LX) 134
Vector bundles, Fock 141
Vector bundles, Virasoro 131 137
Virasoro algebra 132
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



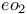 (Hopkins)
(Hopkins) 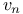 -periodicity
-periodicity  ,
, 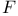
 ,
, 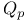
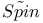 ,
, 
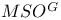


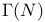

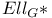 (Devoto)
(Devoto) 
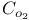
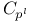
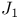
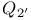
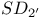

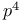
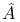
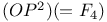
 (double)
(double) 
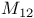
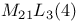 ,
, 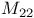
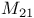
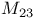
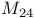

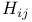
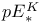 ,
,