|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Samuel P. — Algebraic theory of numbers |
|
|
 |
| Предметный указатель |
Abelian extension VI.1
Algebraic extension II.3
Algebraic over a field II.3
Algebraically closed field II.3
Associates in a ring I.1
Automorphism, Frobenius VI.1 and VI.3
Base of a module I.4
Base, canonical I.4
Bases, dual for the trace II.7
Bezout, identity of I.1
Characteristic of a field I.7
Characteristic polynomial II.6
Classes, ideal III.4
Closure, integral II.1
Conjugate elements or fields II.4
Conjugate prime ideals VI.2
Cyclic extension VI.1
Cyclotomic extension VI.1
Cyclotomic field, polynomial II.9
Decomposition group VI.2
Dedekind ring III.4
Degree, residual V.2
Dependence, equation of integral II.1
Descent, infinite I.2
Diophantinc equation I.2
Discriminant II.7
Discriminant ideal II.7 and V.3
Discriminant, absolute (of a number field) II.8
Domain, fundamental IV.1
Eisenstein’s irreducibility criterion II.9
Equation of integral dependence II.1
Equation of Pell — Fermat IV.6
Equation, Diophantine I.2
Euler’s 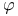 -function I.3 -function I.3
Euler’s criterion V.5
Extension, abelian VI.1
Extension, algebraic II.3
Extension, cyclic VI.1
Extension, cyclotomic VI.1
Extension, Galois VI.1
Extension, quadratic VI.1
Fermat’s equation I.2
Field, cubic II.8
Field, cyclotomic II.9
Field, number (or algebraic number field) II.3
Field, quadratic II.5
Finite type, module of I.4
Fractional ideal III.3
Fractions, ring of V.1
Free module I.4
Frobenius automorphism VI.1 and VI.3
Fundamental units IV.4 and IV.6
Galois extension VI.1
Galois group VI.1
Gaussian integers V.6
Gaussian sum V.5
Greatest common divisor or gcd I.1
Group, decomposition VI.2
Group, Galois VI.1
Group, inertia VI.2
Ideal, discriminant II.7 and V.4
Ideal, fractional III.3
Ideal, integral III.3
Identity, Bezout’s I.1
Imaginary quadratic field II.5
Imbedding of a number field, canoni IV.2
| Index of ramification V.2
Inertia group VI.2
Integer of a number field II.8
Integer or integral over a ring II.1
Integer, Gaussian V.6
Integral closure II.1
Integral dependence equation II.1
Integral ideal III.3
Integrally closed ring II.2
Invariant factors I.5
Lattice in 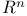 IV.1 IV.1
Law, quadratic reciprocity V.5
Least common multiple or 1cm I.1
Legendrc symbol V.5
Minimal polynomial II.3
Module of finite type I.4
Module, free I.4
Module, Noetherian III.1
Module, torsion-free I.5
Noetherian ring or module III.1
Non-residue, quadratic V.4
Norm II.6
Norm of an ideal III.5
Perfect field II.4
Polynomial, characteristic II.6
Polynomial, minimal II.3
Prime field I.7
Prime ideal III.3
Prime, relatively I.1
Primitive element of an extension II.4
Primitive root modulo p I.7
Primitive root of unity I.6
Principal ideal I.1
Principal ideal ring I.1
Product of ideals III.3
Quadratic extension VI.1
Quadratic field II.5
Quasi-algebraically closed field I.7
Quaternions V.7
Quaternions, Hurwitz V.7
Ramification, index of V.2
Ramified cf.the Supplement
Ramify V.3
Rank of a module I.5
Real quadratic field II.5
Reduced ring IV.7
Relatively prime elements I.1
Remains prime, a prime number or ideal V.4
Represent zero I.7
Residual degree V.2
Residue, quadratic V.4
Ring of fractions V.1
Ring, Dedekind III.4
Ring, Noetherian III.I
Ring, reduced IV.7
Root of unity, primitive I.6
Root, primitive modulo p I.7
Splitting of a prime number V.4
Square-free integer II.5
Sum, Gaussian V.5
Symbol, Legendre V.5
Torsion-free module I.5
Trace II.6
Transcendental element II.3
Units of a number field IV.4
Units of a ring I.1
Volume of a lattice IV.1
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



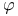 -function
-function