|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Smith L., Meyer D.M. Ч Poincare Duality Algebras, Macaulay's Dual Systems, and Steenrod Operations |
|
|
 |
| ѕредметный указатель |
 88 88
 41Ч42 63Ч64 94 99 160 41Ч42 63Ч64 94 99 160
 41Ч42 63Ч64 94 99 160 41Ч42 63Ч64 94 99 160
 83 83
 81 82 81 82
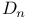 88 89 88 89
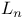 83 85 83 85
 82 82
 94 96 94 96
 94 96Ч97 94 96Ч97
 109 109
 60 60
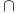 -product 35 36 -product 35 36
 61 61
 56 58 56 58
 101 101
 -operations 33 71 -operations 33 71
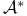 54 54
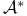 -equivalent 75 -equivalent 75
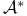 -indecomposable 6 73 93 139 -indecomposable 6 73 93 139
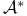 -invariant 64 97 105 109 -invariant 64 97 105 109
 75Ч76 75Ч76
 56 56
 56 56
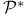 54 54
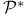 Double Annihilator Theorem see УDouble Annihilator Theorem Double Annihilator Theorem see УDouble Annihilator Theorem
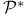 -absorbing 67 -absorbing 67
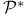 -decomposable 65 -decomposable 65
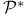 -equivalence class 68 -equivalence class 68
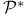 -equivalent 65 -equivalent 65
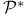 -indecomposable 65 170Ч171 -indecomposable 65 170Ч171
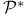 -invariant 65 -invariant 65
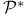 -invariant ideal see УIdeal -invariant ideal see УIdeal
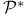 -invariant subalgebra see УSubalgebra -invariant subalgebra see УSubalgebra
 88 89 88 89
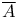 -primary 19 -primary 19
 50 50
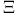 14 15Ч16 41 95 14 15Ч16 41 95
2-adic expansion 102
2-adic valuation 111Ч112
Absorbing subspace 67Ч68
Adem Ч Wu relations 109
Ancestor ideal 17Ч18 38Ч39 133
Ancestor ideal, big 17 18 21 76 137
Ancestor ideal, little 17 137Ч138
Augmentation ideal 9 42
Big ancestor ideal see УAncestor ideal bigФ
Bilinear pairing 10
Binomial coefficient 98
Block parameters 118 121
Boundedness conjecture 74
Canonical anti-automorphism 56 58
Cartan formula 86
Catalecticant 39 133 136 137Ч140 155
Catalecticant equations 137
Catalecticant matrix 7 76 78 136
Cauchy Ч Frobenius lemma 23 24
Change of rings 7 155 157 162
Characteristic classes 60
Cocommutative 65
Cocontraction pairing 155
Codimension one subspace 18Ч19 158
Coexact 50 51 86Ч87 151Ч153 157
Coexact sequence see УCoexactФ
Cofactor matrix 41 84 91
Cofibration 152
Cohen Ч Macaulay 145
Cohen Ч Macaulay algebra 12
Cohomology 95
Coinvariants 81 86
Complete intersection 2 11 141
Comultiplication 32
Conjugacy class 27
Conjugate Mitchell Ч Stong element 167
Conjugate Wu class, total 61 64 117
Conjugate Wu classes 61 62 97 108Ч109 167
Conjugate Wu classes, k-th 61
Conjugate Wu classes, trivial 61 62
Connected sum 11 49 69 138 141
Contraction pairing 36 6
Coproduct 32
CramerТs Rule 43
Cup-product 53
Cyclic 48
D(2) 160 168 170 172
D(3) 173
D(n) 81 85 160 171
Degree one 17
Diagonal 32
Dickson algebra 7 81 85 87 160 168 170Ч173
Dickson algebra, fractal of 87
Dickson coinvariants 6 83 85
Dickson polynomial 6 41 63 81Ч82 85 94Ч96 100 105
Dickson polynomial, formulae for 82
Dickson polynomial, power of 93 95Ч96 105 107Ч109
Dickson Ч Euler class 83
Differential operator 53
Divided power algebra 5 32
Divided power operation 32 33 38
Divided powers see УDivided power operationФ
Double annihilator 12
Double Annihilator Theorem 5 37 58 65 134Ч135
Double Annihilator Theorem, 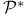 -version 59 67 -version 59 67
Double duality 10
Dual principal system 5 37 40 42Ч44 49 62 89 135
Dual system 5 12 31 35 37 47Ч49
Elementary symmetric polynomial 42Ч43 81
Expansion, dyadic 120
Finite extension 146 148 150Ч151 155Ч156 158 165 169Ч170
Finite type 1
fit 149
Fit extension 149 150Ч151 156 165 169Ч170
Fitness 154
Flat 44Ч45
Formal dimension 1 9 17Ч18 23
Fractal 87
Frobenius automorphism 158
Frobenius functor 44 51
Frobenius homomorphism 5 45 53
Frobenius operator 72
Frobenius periodicity 96 99
Frobenius power 31 41 44 64 77 97 164
Fundamental class 1 6 9Ч10 15 17Ч19 44 47 49 66 68 77Ч78 85Ч86 90 93Ч94 100 131 152 170
G-set 25
Galois field 5 23 41Ч42 53Ч54 56 90
Gorenstein algebra 5 9 12 13 16 57 146 148 150Ч151 155
Hall subgroup 29
Hasse Ч Schmidt differentials 53
Hilbert ideal 81 91
Hit Problem 4Ч7 54 65 74 93 100 123 160
Homogeneous component 94Ч95
Hopf algebra 5 12 31Ч32 35 65 135 162
Ideal quotient 45
Ideal, 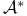 -invariant 93 95Ч97 99 105Ч110 112Ч113 117 128 131 171 -invariant 93 95Ч97 99 105Ч110 112Ч113 117 128 131 171
Ideal, 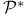 -invariant 54 56 62Ч63 162Ч163 165 169Ч170 -invariant 54 56 62Ч63 162Ч163 165 169Ч170
Ideal, ancestor see УAncestor idealФ
| Ideal, irreducible 4Ч5 7 9 12 13 15Ч19 31Ч32 35 40 42 46 49Ч50 53Ч54 56 62Ч63 90 133 135Ч136 139 146 148 150Ч151 155Ч156 158 163 169Ч170
Ideal, over see УOver idealФ
Ideal, parameter see УParameter idealФ
Ideal, principal 13 15
Ideal, regular 7 12 142 171
Ideals, decreasing chain 97
Indecomposable Poincare duality algebra 11
Index sequence 34
Injective hull 135
Instability condition 161
Integral domain 147
Integrally closed 147
Inverse polynomial 31 133Ч134 137 158
Inverse polynomial algebra 134
Inverse principal system 135
Inverse system 5 31 135 156 158 163 170
Involution 16 27 38 41 95
Irreducible ideal see УIdeal irreducibleФ
Isomorphism classes 19
Isotropy subgroup 22
Jordan form 24
Krull dimension 146
Lighthouse 95 100
Linear form 57
Little ancestor ideal see УAncestor ideal littleФ
Lying over 7 145Ч146 148
m-primary ideal 51
Macaulay dual 6 37 41Ч42 47Ч48 85
Macaulay dual of the ideal  101 101
Macaulay dual of the ideal  101Ч102 101Ч102
Macaulay inverse 135
MacaulayТs double annihilator correspondence 37
MacaulayТs Double Annihilator Theorem see УDouble Annihilator TheoremФ
MacaulayТs dual principal system see УDual principal systemФ
MacaulayТs inverse system 135
Map of degree one 17
Middle associative 10
Middle dimension 100
Mitchell Ч Stong element 167
Mitchell Ч Stong element, conjugate see УConjugate Mitchell Ч Stong elementФ
Modular case 2
Module of 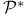 -indecomposables 65 -indecomposables 65
Moduli space 19 23
MolienТs theorem 27
Monomial 66 68 70 72 75 78 89 93Ч94 138
Monomial action 70
Monomial ideal 37 42
Nil radical 32
Node 94
Noether Isomorphism Theorem 44
Noetherian algebra 15
Nondecreasing sequence 100
Nondegenerate 10
Number theoretic function 111
Obstruction 109
Orbit 22 26 39 88
Orbit space 19 23
Over ideal 14 41
P 49 71 74 77
p-adic expansion 34
Palindromic 37 137
Paradigm,  5 31 40 88Ч89 113 5 31 40 88Ч89 113
Parameter ideal 12 13 16 41 47 55 57 145 148Ч149 151 159
Parameter ideal, 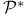 -invariant 55 -invariant 55
Periodicity map 74
Periodicity operator 49 71 74 77 100
Poincare dual 15Ч17 35 131 152 154
Poincare duality 17Ч23 26Ч29 31 35 37Ч40 44 49 51 53Ч54 57Ч58 60Ч63 65Ч66 68Ч70 73Ч74 76Ч79 81 83 85Ч86 90 93Ч94 99Ч100 105 123 131 146Ч148 151Ч154 158 160 164 168
Poincare duality algebra 1 2 5 9 11 17Ч23 26Ч29 31 35 37Ч40 44 49Ч51 53Ч54 57Ч58 60Ч63 65Ч66 68Ч70 73Ч74 76Ч79 81 83 85Ч86 90 93Ч94 99Ч100 105 123 131 146Ч148 151Ч154 158 160 164 168 173
Poincare duality quotient 6 17Ч18 21 23 39 49 53Ч54 63 65Ч66 70 73 77 79 90 93 95 100 170
Poincare duality quotient of ![$\mathbb{F}[V]$](/math_tex/9bbba2985617e266a41eefcc59f9cd6b82.gif) 12 12
Poincare polynomial 95
Poincare series 20 27Ч28 99 137 141
Polynomial algebra 155Ч156
Prime ideal 7 146
Primitive element, Milnor 83
Principal 47
Principal ideal see УIdeal principalФ
Projective space 19
Pseudoreflection group 2
Rank 12
Rank of a Poincare duality quotient of ![$\mathbb{F}[V]$](/math_tex/9bbba2985617e266a41eefcc59f9cd6b82.gif) 12 12
Rank sequence 138
Regular ideal see УIdeal regularФ
Regular sequence 12 49 66 81 86Ч87 94 142 145 148
Relative transfer 148
Ring extension, finite see УFinite extensionФ
Ring of invariants 81
Row-echelon form 137
Spike 6 93
Split 50Ч51 147Ч148 151Ч152
Sq 64 94
Steenrod algebra 4Ч7 53Ч54 58 66 79 100 160 163 169Ч170
Steenrod operation, total 56 57 71 105 109
Steenrod operations 7 54 66 71
Steenrod square, total 64
Steinberg, R. 2
Stiefel Ч Whitney class, power of 93
Stiefel Ч Whitney classes 6 62 93 123
Stong Ч Tamagawa formulae 82
Stripping operation 35
Subalgebra, 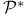 -invariant 86Ч87 -invariant 86Ч87
Subspace, codimension one see УCodimension one subspaceФ
Support 36 70 78
Sylow subgroup 29
symmetric 10
Symmetric coinvariants 6
System of parameters 12 42 146 148
Thom class 56 57 63Ч64 66 95Ч96 105 109 165
Thom Ч Wu formulae 4
Topological space 95
Total Steenrod operation see УSteenrod operation totalФ
Total Steenrod square see УSteenrod square totalФ
Totalization 13
Transition element 14 15 41 43 142 149 151
Transition invariant 14
Transitive 155
Transversal 27
Trivial conjugate Wu classes see УConjugate Wu classes trivialФ
Trivial Wu classes see УWu classes trivialФ
Type, finite 1
Unstable algebra 53Ч54 56 163
Unstable algebra (over 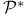 ) 54 ) 54
Unstable Poincare duality algebra 54
Unstable polynomial agebra 162 169Ч170
Upper triangular 141
Wu class 5Ч6
Wu class, total 60 64 170
Wu class, total conjugate 61
Wu classes 3 60 64 66 68 71 77 83 86 90 165
Wu classes, conjugate see УConjugate Wu classesФ
Wu classes, k-th 60
Wu classes, nontrivial 99
Wu classes, trivial 54 60 61 63 65 68Ч70 73 79 86 93Ч99 105Ч109 121 123 125 128 131 169Ч170 173
Wu Wen Tsuen 54
WuТs formula 124Ч125
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте








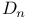
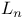





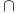 -product
-product 


 -operations
-operations 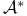



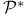

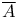 -primary
-primary 



![$\mathbb{F}[V]$](/math_tex/9bbba2985617e266a41eefcc59f9cd6b82.gif)