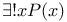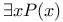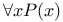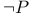|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Velleman D.J. — How to Prove It: A Structured Approach |
|
|
 |
| Предметный указатель |
 -notation 281—282 -notation 281—282
Absorption laws 21
Antecedent 44
antisymmetric 189
Arbitrary object 108
Arithmetic mean 276
Arithmetic-geometric mean inequality 276
Associative laws 22 23
Associative laws for 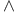 and and 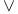 21 25 21 25
asymmetric 210
Bernstein, Felix 322
Biconditional 23 52 53
Biconditional, truth table for 23 52
Big-Oh 235
Bijecuon 182 242
Binary relation 182 242
Binomial coefficient 288
Binomial theorem 260 288
Bound variable 29
Bounded quantifier 57 68
Canior — Schroeder — Bernstein Theorem 322—327
Canter's Theorem 318 320 321
Cantor, Georg 318
Cardinality 307
Cartezian product 163—171
cases 136
Closure of a set under a function 303
Closure, reflexive 202
Closure, reflexive symmetric 212
Closure, symmetric 204
Closure, symmetric transitive 212
Closure, transitive 204 209 300
Cohen, Paul 327
Commutative laws for 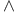 and and 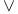 21 23 52 21 23 52
Compatible 225 236
composition 177 178 182 231 300
Conclusion 8 85
Conditional laws 44—45 47 50
Conditional, antecedent of 44
Conditional, consequent of 44
Conditional, truth table for 44—45 47
Congruent 213
Conjecture 2
Conjunction 10
Connective symbol 10
Consequent 44
Constant function 235 244
Continuum Hypothesis 326—327
Contradiction 22 23 26 32 41
Contradiction law 23
Contradiction, proof by 96 97 98 99
Contrapositive 49 91
Contrapositive law 49
CONVERSE 49
Coordinate 163
Countable set 310
Counterexample 2 85
DeMorgan's law 20 21 22 23 25 39 47 50
Denumerable set 318 326
Diagonalization 320
Difference of sets 34
Directed graph 183
Disjoint 40
Disjoint pairwise 153 214
Disjunction 10
Disjunctive syllogism 142
Distributive laws 38—39
Distributive laws for 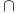 and and 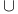 38—39 38—39
Distributive laws for  70 70
Distributive laws for 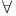 and and 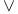 70 70
Distributive laws for 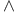 and and 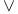 21 23 21 23
divides 121
Division algorithm 290 291
Domain 172 230
Double negation law 21 22 23: 47
EDGE 181
Element 27
Empty set 32
Equintimerous sets 306—312
Equivalence class 214 215
Equivalence relation 213—222 309
Equivalent formulas 19 21
Even integer 134 312
Exclusive cases 138
Exclusive OR 15 24
Exhaustive cases 136
Existential instantiation 115
Existential quantifier 55 58
Factorial 282
Family of sets 75
Fermat numbers 276
Fermat, Pierre de 276
fibonacci 291
Fibonacci numbers 291—293 297
Finite sequence 317 321—322
Finite set 306
Fixed point 255
Formula 12
Free variable 28 55
Function, compatible with an equivalence relation 225
Function, composition of 232—233
Function, domain of 230
Function, function of 229
Function, identity 227
Function, inverse of 245—252
Function, one-to-one 236
Function, onto 236
Function, range of 239
Function, restriction of 234 243
Geometric mean 357
Gihonacci sequence 297
givens 88
Goal 88
Goedel, Kurt 327
Graph 183
Greatest common divisor 299
Greatest lower bound (g.l.b.) 197
Harmonic mean 277
Harmonic numbers 286
Hilbert, David 326
Hypothesis 85
Idempolent laws 21 22
Identity relation 183 203—204 213
IFF 52
Image 227 230 255—259
Inclusion-Exclusion Principle 369
Inclusive or 15
INDEX 74
Index set 74
Indexed family 74 75
Induction step 260 270
Induction, strong 288—295
Inductive hypothesis 263 268 272
Inference, rule of 107
Infinite sets 306
Injections 236
Instance of a theorem 85
Integers 31 32
Intersection of family of sets 77 78
Intersection of indexed family of sets 79
intersection of two sets 34
interval 31 328
Inverse 173 245—252
| Inverse image 255—259
Irrational number 161—162
Irrefiexive 204
largest element 197
Least upper bound 197
Lemma 217
LIMIT 161
Logarithm 252
Loop 184
Lower bound 197
Lucas numbers 297
Lucas, Edouard 297
Main connective 17
Mathematical induction See induction
Maximal element 197
Mersenne, Marin 5
Minimal element 192 267—269
MODULO 215 221
modus ponens 103
Modus Tollens 103 104 105 107
NAND 24
Natural number 31
Necetttiuy condition 50
Negation 10
NOR 24
Null set 32
Odd integer 24 133 134
One-to-one 236
One-to-one correspondence 242
Onto 236
Ordered pair 163—171
Ordered triple or quadruple 169
Pairwise disjoint 153 214
Partial order 190 254 267 268—269 314
Partial order, strict 211
Partition 214 215
Pascal's triangle 288
Pastil, Blaise 288
Perfect number 5
Pigeonhole Principle 313
Polynomial 299
Power set 75—76 119 318
Premise 8
Preorder 225
Prime number 1 74 94 156—158
Prime number, largest known 5
Prime number, Mersenne 5
Prime number, twint 6
proof 1 84
Proof by cases 137
Proof by contradiction 96 97 98 99
Proof Designer 102 373—374
Proof Designer, Preface and Appendix 373—374
Proof strategy for a given of the form, 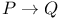 102 102
Proof strategy for a given of the form, 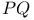 126 126
Proof strategy for a given of the form, 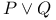 142—143 142—143
Proof strategy for a given of the form, 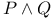 124 124
Proof strategy for a given of the form, 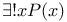 152 152
Proof strategy for a given of the form, 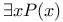 115 115
Proof strategy for a given of the form, 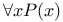 115 115
Proof strategy for a given of the form, 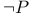 99—100 102 99—100 102
Proof strategy for a goal of the form, 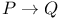 88 90 91 88 90 91
Proof strategy for a goal of the form, 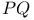 126 126
Proof strategy for a goal of the form, 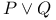 138 141—142 138 141—142
Proof strategy for a goal of the form, 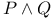 124 124
Proof strategy for a goal of the form, 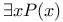 , , 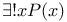 149 149
Proof strategy for a goal of the form, 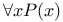 , , 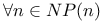 260 289 260 289
Proof strategy for a goal of the form, 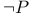 95 96 95 96
Proper subset 203
Quantifier 55—64
Quantifier, bounded 68 57
Quantifier, existential 58
Quantifier, negation laws 65 66 69
Quantifier, unique existential 146
Quantifier, universal 55
Quotient 290
RANGE 173 239
Rational number 31 311 326 328
Real number 31
Recursive definition 280
Recursive procedure 274
Refine 225
Reflexive 184
Reflexive closure 202
Reflexive symmetric closure 212
Relation, antisymmetric 212
Relation, asymmetric 210 346
Relation, binary 182 242
Relation, composition of 176 180—181
Relation, domain of 173
Relation, identity 183 203—204 213
Relation, inverse of 173
Relation, irreflexive 204
Relation, range of 311
Relation, reflexive 184
Relation, symmetric 184
Relation, transitive 184
Remainder 290 139—140
Restriction 234 243
Rule of inference 107
Russell's paradox 83
Russell, Bertrand 83
Schroeder, Emst 322
SEQUENCE 297—298
Set 27. See also countable set; denumerable set; empty set (or null set); family of sets; finite set; index set infinite
Smallest element 184
Strict partial order 204
Strict total order 204
Strictly dominates 322
Strong induction 288—295
Subset 40 184
Subset, proper 203
Sufficient condition 50
Surjection 236
Symmetric closure 204 205
Symmetric difference 36 43 154
Symmetric transitive closure 40 212 184
Tautology 23
Tautology laws 23
Theorem 85
Total order 190 269—270 275
Total order, strict 204
Transitive closure 204
Trichotomy 204
Truth set 27 30 37 163
Truth table 14—23
Truth value 14
Uncountable set 315—321
Union of a family of sets 78
Union of an indexed family of sets 79
union of two sets 78
Universal instantiation 15
Universal quantifier 55
Universe of discourse 31 328
Upper bound 197
Vacuously true statement 70
Valid argument 9
Variable 26
Variable, bound 29
Variable, free 28 55
Venn digram 36 40—41
Vertex 182
Well-formed formula 12
Well-ordered principle 294 295 299
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -notation
-notation 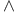 and
and 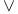
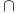 and
and 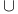

 and
and