|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Joyce D.D. Ч Riemannian holonomy groups and calibrated Geometry |
|
|
 |
| ѕредметный указатель |
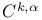 see УHolder spaceФ see УHolder spaceФ
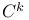 space 5 space 5
 holonomy 54Ч55 227Ч239 holonomy 54Ч55 227Ч239
 holonomy, associative 3-fold 68 71 72 254Ч272 holonomy, associative 3-fold 68 71 72 254Ч272
 holonomy, coassociative 4-fold 68 71 72 254Ч272 holonomy, coassociative 4-fold 68 71 72 254Ч272
 holonomy, compact manifolds, Betti numbers of 238 holonomy, compact manifolds, Betti numbers of 238
 holonomy, compact manifolds, constructing 233Ч239 holonomy, compact manifolds, constructing 233Ч239
 holonomy, compact manifolds, moduli space of 232 253 holonomy, compact manifolds, moduli space of 232 253
 holonomy, compact manifolds, topology of 230Ч232 holonomy, compact manifolds, topology of 230Ч232
 holonomy, explicit metrics 253 holonomy, explicit metrics 253
 holonomy, holonomy subgroups 230 holonomy, holonomy subgroups 230
 holonomy, metrics Ricci-flat 229 holonomy, metrics Ricci-flat 229
 holonomy, parallel spinors 230 holonomy, parallel spinors 230
 instanton 253 instanton 253
 , definition 227 , definition 227
 -manifold 228 -manifold 228
 -manifold, with holonomy SU(2) or SU(3) 230 -manifold, with holonomy SU(2) or SU(3) 230
 -structure 228 252 -structure 228 252
 -structure, function -structure, function  228 228
 -structure, nearly parallel 253 -structure, nearly parallel 253
 -structure, positive 3-form 228 253 -structure, positive 3-form 228 253
 -structure, positive 4-form 228 -structure, positive 4-form 228
 -structure, small torsion 233 235 -structure, small torsion 233 235
 -structure, splitting of forms 229 231 -structure, splitting of forms 229 231
 -structure, torsion 228 -structure, torsion 228
 -structure, torsion-free 228 233 236 -structure, torsion-free 228 233 236
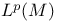 see УLebesgue spaceФ see УLebesgue spaceФ
 see УSobolev spaceФ see УSobolev spaceФ
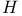 see УQuaternionsФ see УQuaternionsФ
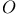 see УOctonionsФ see УOctonionsФ
* see УHodge starФ
3-Sasakian manifold 222Ч223
3-Sasakian quotient construction 225
A-genus 64 216 242
A-model 184
Affine structure 168 194
Affine structure, integral 195 197 198
Age grading 131Ч133
ALE manifold, Calabi Ч Yau 234 250Ч251
ALE manifold, Eguchi Ч Hanson space 205Ч206 212 234 246
ALE manifold, hyperkahler 201 205Ч207
ALE manifold, Spin(7) 250Ч251
Almost Calabi Ч Yau m-folds 165Ч166
Almost Calabi Ч Yau m-folds, generic 166 173 177 199Ч200
Ambrose Ч Singer Holonomy Theorem 31 36
Associative 3-folds 68 71 72 254Ч272
Associative 3-folds, deformations 256
Associative 3-folds, examples 259Ч264 268Ч270
Associative 3-folds, ruled 261Ч262
Associative cones 258 260 263
Associative cones, and pseudoholomorphic curves in 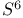 258 261 262 258 261 262
Associative cones, as an integrable system 261
Associative cones, two-sided 258
Associative fibrations 272
Asymptotic cone 152
Asymptotically conical SL m-folds 152 161Ч165
Asymptotically conical SL m-folds, deformations 162
Asymptotically conical SL m-folds, examples 155Ч157 163Ч165
Asymptotically cylindrical manifold 237
Asymptotically Locally Euclidean see УALE manifoldФ
Atiyah Ч Singer index theorem 18 64 242 275
B-model 184
Berger's theorem 52
Betti number 2 238 248 252
Betti number, refined 59 231 243
Bianchi identities 34 41 43 56
Blow-up 93Ч94
Bochner theorem 60 125
Bootstrap method 117
Brane 180 183 184
Calabi Conjecture 54 85 100Ч121 211 234 237 239
Calabi Ч Yau manifold 54 68 85 100 122Ч145 239
Calabi Ч Yau manifold, A-model 184
Calabi Ч Yau manifold, almost 165Ч166 173 177 199Ч200
Calabi Ч Yau manifold, B-model 184
Calabi Ч Yau manifold, constructions 139Ч144
Calabi Ч Yau manifold, definition 126
Calabi Ч Yau manifold, deformations 144Ч145
Calabi Ч Yau manifold, Hodge numbers 126
Calabi Ч Yau manifold, mirror pair 143 180 183
Calabi Ч Yau orbifold 136
Calibrated geometry 65Ч74 146Ч177 254Ч277
Calibrated submanifold 67
Calibration 67 126
Calibration, classification on  69Ч72 69Ч72
Canonical bundle 96
Cartan Ч Kahler theory 147 153
Category 184Ч185
Category, abelian 185Ч186
Category, additive 185
Category, Ax- 187
Category, Calabi Ч Yau 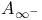 190 190
Category, definition 184
Category, derived 186Ч187
Category, derived Fukaya 184 189
Category, dg- 187
Category, enhanced triangulated 190
Category, equivalence 184 185
Category, exact 185
Category, Fukaya 184 187Ч189
Category, functor 184
Category, linear 185
Category, ofcoherent sheaves 184 185 187
Category, triangulated 186Ч187
Category, triangulated 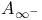 187 189Ч190 187 189Ч190
Cayley 4-folds 68 71 272Ч277
Cayley 4-folds and associative 3-folds 274
Cayley 4-folds and coassociative 4-folds 274
Cayley 4-folds and holomorphic surfaces 273
Cayley 4-folds and SL 4-folds 273
Cayley 4-folds and Spin(7) instantons 277
Cayley 4-folds, 2-ruled 274
Cayley 4-folds, deformations 273
Cayley 4-folds, examples 273Ч276
Cayley 4-folds, with isolated conical singularities 276
Cayley fibrations 276Ч277
Cayley integral current 277
Cayley numbers see УOctonionsФ
Characteristic class 96
Characteristic class, A-genus 64 216 242
Characteristic class, first Chern class 96 99 100 123
Characteristic class, first Pontryagin class 232 242 244
Cheeger Ч Gromoll Theorem 61
Chow's theorem 92 97 126
Closed string mirror symmetry 181Ч183 190Ч191
Closed strings 180
Coassociative 4-folds 68 71 72 254Ч272
Coassociative 4-folds, 2-ruled 263Ч264
Coassociative 4-folds, asymptotically conical 263
Coassociative 4-folds, deformations 257
Coassociative 4-folds, examples 259Ч264 268Ч270
Coassociative 4-folds, with isolated conical singularities 270Ч271
Coassociative cones 258 261
Coassociative cones, 2-ruled 263
Coassociative fibrations 271Ч272
Coherent sheaf 184 185 187 190
Cohomology, de Rham 2
Cohomology, Dolbeault 81
Cohomology, Hodge numbers 87
Cohomology, ofsheaves 91 95
Cohomology, other cohomology theories 2
Cohomology, Poincare duality 2 131 132 134 168 232
Compact linear map 6 104
Complete intersection 140
Complex manifold 76Ч79
Complex manifold, biholomorphism 78
Complex manifold, holomorphic function 76
Complex manifold, holomorphic map 78
Complex manifold, rigid 94 133 140
Complex projective space 77
| Complex projective space, weighted 134 135 141Ч142 181 190 249
Complex structure 76Ч77
Complex structure, almost 76
Complex symplectic manifold 214Ч216
Complex symplectic manifold, irreducible 214
Complex symplectic manifold, marked 215
Complex symplectic manifold, moduli space 215
Connection 19Ч24
Connection, Levi-Civita 39Ч41
Connection, on principal bundle 22
Connection, on tangent bundle 32Ч36
Connection, on vector bundle 21
Connection, torsion-free 34Ч36
Continuity method 106
Crepant resolution 127Ч133
Current 72
Current, calibrated 73
Current, Cayley 277
Current, integral 72
Current, rectifiable 72
Current, special Lagrangian 158 176
Curvature, and holonomy groups 30Ч32
Curvature, in principal bundles 23
Curvature, in vector bundles 21Ч22
Curvature, of Kahler metrics 84Ч85
Curvature, Ricci 42
Curvature, Riemann 40Ч43 45 50 52 56 58 84 112 125 229 232 235 236 244 247
Curvature, scalar 42
de Rham theorem 2
Deformation 94Ч95
Deformation, of 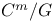 133 133
Deformation, of Calabi Ч Yau manifold 144Ч145
Deformation, smoothing 94
Deformation, universal 95
Deformation, versal 95
Derived category 186Ч187
Derived category, of coherent sheaves 184 187
Derived Fukaya category 169 184
Dg-category 187
Dirac operator 62Ч64 242 243
Discriminant 191
Discriminant, trivalent graph 196
Divisor 98Ч99
Divisor, exceptional 94 128
Divisor, prime 98
Dolbeault cohomology 81
Double point 128
Double point, ordinary 129
Double point, rational 130
Eguchi Ч Hanson space 205Ч206 212 234 246
Elliptic operator 7Ч18
Elliptic operator,  estimate 13 estimate 13
Elliptic operator, definition 9 11
Elliptic operator, existence of solutions 16Ч18
Elliptic operator, kernel finite-dimensional 16
Elliptic operator, nonlinear 9 102
Elliptic operator, regularity 12Ч15 66 74 116 121 162 167 171 237 258 266
Elliptic operator, Schauder estimate 13Ч14
Elliptic operator, symbol 9 11
Embedding 65
Enhanced triangulated category 190
Equivalence of categories 185
Exterior differential systems 54 147 153 252 256 264 270 273
Exterior form see УFormФ
Fano variety 180 190 221
Floer homology, Lagrangian 189
Floer homology, obstructions 169 188Ч189
FLOP 129
FORM 1Ч4
Form, complex symplectic 203
Form, G-structure splitting 56Ч58
Form, Hermitian 82
Form, holomorphic volume 123 126
Form, hyperkahler 2-form 203
Form, Kahler 82 123
Form, of type (p, q) 80
Form, on Kahler manifolds 85Ч86
Frobenius theorem 46
Fukaya category 169 184 187Ч189
Fukaya category, derived 189
functor 184 190
Functor, (left or right) derived 186
Functor, (left or right) exact 186
G-structure 36
Geometric measure theory 72Ч74 158 170 171 176 277
Green's representation 14
Gromov Ч Hausdorff limit 197
Gromov Ч Witten invariants 182Ч183 191
Hilbert scheme 218
HMS Conjecture 184 187Ч190
Hodge numbers 87
Hodge numbers, of hyperkahler manifolds 216
Hodge star 3 57
Hodge star, on Kahler manifolds 86
Hodge theory 3Ч4 58Ч60
Hodge theory, on Kahler manifolds 86Ч88
Holder space 5Ч6
Holder's inequality 4
Holomorphic vector bundle 81 185
Holomorphic volume form 126
Holonomy algebra 27 29 43
Holonomy group and cohomology 56Ч61
Holonomy group and curvature 30Ч32
Holonomy group, classification 52Ч56
Holonomy group, constant tensors 32Ч34
Holonomy group, definition 25 28 42
Holonomy group, exceptional see У holonomyФ Holonomy УSpin(7) etc. holonomyФ Holonomy УSpin(7) etc.
Holonomy group, for principal bundles 28Ч30
Holonomy group, for vector bundles 24Ч28
Holonomy group, restricted 26 28 42
Holonomy group, Ricci-flat 55
Holonomy group, Riemannian 42Ч43
Homological mirror symmetry 183Ч191
Homological mirror symmetry conjecture see УHMS ConjectureФ
Hypercomplex algebraic geometry 224
Hypercomplex manifold 223Ч224
Hypercomplex quotient construction 225
Hyperkahler manifold 54 100 201Ч219
Hyperkahler manifold, ALE 201 205Ч207
Hyperkahler manifold, cohomology 217
Hyperkahler manifold, examples 218Ч219
Hyperkahler manifold, Hodge numbers 216
Hyperkahler manifold, moduli space 217
Hyperkahler manifold, twistor space 204Ч205
Hyperkahler quotient construction 207 224
Hyperkahler structure 201 203
Hypersurface 98
Hypersurface, Calabi Ч Yau 140
Hypersurface, degree d 140
Hypersurface, in toric variety 143
Hypersurface, in weighted projective space 141Ч142
Immersion 65
Implicit Mapping Theorem 7
Injectivity radius 5 173 235 236 247
Instanton 225 253
Integrable systems 152Ч153 155 159 177 260Ч261
Integral affine structure 195 197 198
Integral current 72
Integral current, Cayley 277
Integral current, special Lagrangian 158 171 176
Interior estimate 15
Intrinsic torsion 38
Inverse mapping theorem 7 119
K3 surface 208Ч213
K3 surface, examples 208
K3 surface, marked 209
K3 surface, moduli space 209 213
Kahler chamber 210
Kahler class 84 88
Kahler cone 88 210 216
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



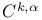
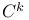 space
space  holonomy
holonomy 
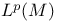

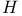
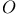
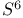

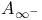
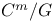
 estimate
estimate