|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Monk P. — Finite Element Methods for Maxwell's Equations |
|
|
 |
| Предметный указатель |
 -coercivity 26 -coercivity 26
A posteriori error estimate 355
A posteriori error estimate, duality estimate 359
A posteriori error estimate, numerical results 363
A posteriori error estimate, residual estimate 361
ABC see “Absorbing boundary condition”
Absorbing boundary condition 11 365
Absorbing boundary condition, error estimate 366
Annihilator 19
Arithmetic geometric mean inequality 16
Assumptions on data, coefficients 83
Assumptions on data, domain 83
Assumptions on data, impedance 84
Assumptions on data, source fields 84
Asymptotic expansion of  233 233
Babuska — Brezzi condition, continuous 22
Babuska — Brezzi condition, discrete 27
Backscattered RCS 392
Barycentric coordinate 109
Bessel differential equation 236
Bessel differential equation, spherical 239
Boundary component map see “Caldcron operator”
Boundary condition, impedance 9
Boundary condition, perfectly conducting 9
Boundary inverse estimate 152
Boundary projection 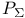 211 211
Boundary spaces 150
Boundary to far field map 23 419
Buried object see “Scattering problem layered
Calderon Extension 40
Calderon operator, electric-to-magnetic 249
Calderon operator, exterior coercive  251 251
Calderon operator, exterior elcctric-to-magnetic  249 249
Calderon operator, exterior magnetic-to-electric  253 253
Calderon operator, interior magnetic-to-clectric 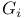 253 253
Calderon operator, interior magnetic-to-clectric 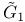 254 254
Calderon operator, magnetic-to-clectric 252
Carding inequality 171
Cartesian coordinates 425
Cauchy — Schwarz inequality 16
Cavity problem 12
Cavity problem, collective compactness 180
Cavity problem, discrete 168
Cavity problem, eigenvalues, continuous 13 96
Cavity problem, eigenvalues, discrete 195
Cavity problem, ellipticized 189
Cavity problem, ellipticized, discrete 191
Cavity problem, error analysis via collective compactness 176
Cavity problem, error analysis via duality 168
Cavity problem, error estimate 169 187
Cavity problem, existence 95
Cavity problem, numerical results 188
Cavity problem, scalar potential 89
Cavity problem, uniqueness 92
Cavity problem, variational 83
Cavity resonances see “Cavity problem eigenvalues”
Cea’s lemma 25
Clement interpolant 147
Clement macro-element 147
Closed Hilbert space 17
Closure 17
Collectively compact 32
Compact imbedding, 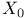 into into  87 87
Compact imbedding,  into into  286 286
Compact imbedding,  into into  268 268
Conditioning for small  193 193
Conductivity 6
Conforming finite element 105
Constitutive equations 5
Continuity required of elements 107
Continuous elements, danger 191
Curl 50
Curved domains 209 213
Curved domains, large elements 214
Curved domains, method of Dubois 210
de Rham diagram, continuous 65
de Rham diagram, discrete 149
Debye potential 235
Degrees of freedom, 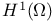 conforming, hexahedra 162 conforming, hexahedra 162
Degrees of freedom, 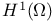 conforming, hp 219 conforming, hp 219
Degrees of freedom, 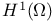 conforming, tetrahedra 143 209 conforming, tetrahedra 143 209
Degrees of freedom, curl conforming, hexahedra 158
Degrees of freedom, curl conforming, hp 220
Degrees of freedom, curl conforming, tetrahedra 129 205
Degrees of freedom, definition 102
Degrees of freedom, divergence conforming, hexahedra 156
Degrees of freedom, divergence conforming, hp 222
Degrees of freedom, divergence conforming, tetrahcdra 119 202
Degrees of freedom, shorthand 102
Dense subspace 17
Density, 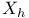 in X 178 in X 178
Deny — Lions Theorem 109
Dielectric 6
Dipole source, explicit formula 411
Dipole source, free space 305
Dipole source, half space 316
Dipole source, horizontal polarization 325
Dipole source, vertical polarization 322
Discrete compactness 181 292
Discrete compactness of 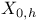 183 184 183 184
Discrete divergence 192
Discrete divergence-free 170
Discrete divergence-free, approximation by divergence-free 173
Discrete Helmholtz decomposition 170 177
Dispersion error see “Phase error”
Distributional derivative 37
Divergence 50
Divergence theorem 50
Domain 37
Dot product 2
DtN map see “Calderon operator”
Dual pairing 19
Dual space 19
Duality estimate 174
Dyadic Green’s function see “Green’s dyadic”
Edge element 127 158 219
Edge element, linear 139
Edge element, quadratic 140
Eigenfunction 24
Eigenvalue 24
Element size parameters: 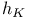 and and 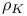 112 112
Enhanced elements 199
Euclidean norm 2
Far field equation 397
Far field operator F 397
Far field pattern 233
Far field recovery 386
Finite covering 336
Finite element spaces on curved domains 216
Finite element spaces, 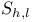 336 336
Finite element spaces, 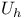 145 163 145 163
Finite element spaces,  209 209
Finite element spaces,  219 219
Finite element spaces, 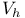 134 159 134 159
Finite element spaces,  207 207
Finite element spaces, 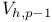 220 220
Finite element spaces, 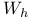 124 157 124 157
Finite element spaces, 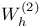 204 204
Finite element spaces,  221 221
Finite element spaces, 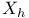 168 168
Finite element spaces, 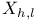 336 336
Finite element spaces,  149 164 149 164
Finite element spaces, 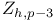 222 222
Finite element, general definition 101
Finite elements, 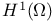 conforming, hexahedra 162 conforming, hexahedra 162
Finite elements, 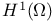 conforming, hp 218 conforming, hp 218
Finite elements, 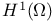 conforming, tetrahedra 143 209 conforming, tetrahedra 143 209
Finite elements, 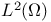 conforming, hexahedra 164 conforming, hexahedra 164
Finite elements, 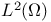 conforming, tetrahedra 149 conforming, tetrahedra 149
Finite elements, curl conforming, hexahedra 158
| Finite elements, curl conforming, hp 219
Finite elements, curl conforming, tetrahcdra 126 205
Finite elements, divergence conforming, hexahedra 155
Finite elements, divergence conforming, hp 221
Finite elements, divergence conforming, tetrahedra 118 202
Finite elements, one dimensional 101
Finite elements, one dimensional, estimates 106
First family of elements, hexahedra 155
First family of elements, tetrahedra 99
Fourier space, error estimate 289
Fourier space, inverse estimate 290
Fourier space, on  289 289
Fredholm alternative 24
Friedrichs inequality 72 88 185
Function spaces, classical, 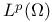 36 36
Function spaces, classical, 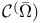 36 36
Function spaces, classical,  36 36
Function spaces, classical, 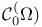 36 36
Function spaces, polynomial,  , ,  212 212
Function spaces, polynomial, 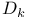 119 119
Function spaces, polynomial, 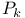 , ,  108 108
Function spaces, polynomial, 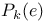 , , 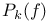 108 108
Function spaces, polynomial,  109 109
Function spaces, polynomial, 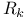 128 128
Function spaces, polynomial, 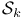 128 128
Function spaces, polynomial,  108 108
Function spaces, Sobolev, 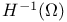 42 42
Function spaces, Sobolev, 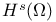 38 38
Function spaces, Sobolev, 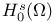 38 38
Function spaces, Sobolev,  44 44
Function spaces, Sobolev, 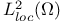 45 45
Function spaces, Sobolev, 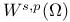 37 37
Function spaces, Sobolev, 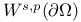 43 43
Function spaces, Sobolev, 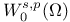 38 38
Function spaces, Sobolev, 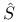 286 286
Function spaces, Sobolev, 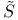 265 265
Function spaces, Sobolev, S 85
Function spaces, vector, 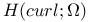 55 55
Function spaces, vector, 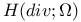 52 52
Function spaces, vector,  55 55
Function spaces, vector, 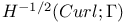 59 59
Function spaces, vector, 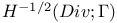 59 59
Function spaces, vector, 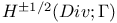 244 244
Function spaces, vector, 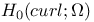 55 55
Function spaces, vector, 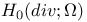 54 54
Function spaces, vector,  69 69
Function spaces, vector, 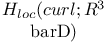 230 230
Function spaces, vector,  67 67
Function spaces, vector,  67 67
Function spaces, vector, 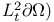 48 48
Function spaces, vector,  , ,  , ,  , , 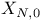 , , 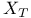 , , 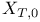 71 71
Function spaces, vector, 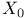 86 86
Function spaces, vector,  58 410 58 410
Function spaces, vector,  286 286
Function spaces, vector, 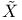 263 263
Function spaces, vector,  267 267
Function spaces, vector, X 82
Fundamental solution  225 225
Funk Hecke formula 241
Generalized Lax — Milgram lemma 21
Generous overlap 336
Geometric constraints on elements 112
Gradient 43
Green’s dyadic 303
Green’s dyadic, discrete, admissible 307
Green’s dyadic, layered medium 321
Green’s dyadic, layered medium, first column 325
Green’s dyadic, layered medium, third column 322
Green’s dyadic, perfectly conducting half space 316
H-independent uniformity 336
Health warning 399
Helmholtz decomposition 65 69 86 267 286
Herglotz wave function 398 414
Herglotz wave function, approximation property 415
Herglotz wave function, characterization 414
Herglotz wave function, uniqueness 414
Hertz vector 321
Hilbert space 16
Hilbert space, compact 23
Hilbert space, relatively compact 23
Hilbert — Schmidt theorem 24
Hodge operator 172
hp-finite elements 217
Ill-posed/well-posed 399
Imbedding 40
Incident field 9
Infinite element method 370
Infinite element method, discrete problem 374
Inner product, boundary, 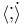 82 82
Inner product, boundary,  44 44
Inner product, volume,  49 49
Integral identities 50
Interface condition 8
Interior cut 65
Interpolant, definition,  134 160 207 134 160 207
Interpolant, definition, 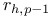 220 220
Interpolant, definition,  124 157 204 124 157 204
Interpolant, definition,  222 222
Interpolant, definition,  145 163 145 163
Interpolant, definition,  219 219
Interpolant, definition,  148 148
Interpolant, error estimate,  136 160 208 136 160 208
Interpolant, error estimate,  124 157 204 124 157 204
Interpolant, error estimate,  163 163
Interpolant, error estimate,  145 164 145 164
Interpolant, error estimate,  149 149
Inverse problem 394
Inverse problem, linear sampling method 397
Inverse problem, uniqueness 411
Jacobi — Anger expansion 241
Jump across a face ![$[\dot]_N$](/math_tex/1c0a583884211410cb3ba4edd0a80a2682.gif) 359 359
Jump across a face ![$[\dot]_T$](/math_tex/2ce036c29ce8ca8cdabbc3b00083db8882.gif) 358 358
Laplace — Beltrami operator 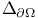 49 49
Lax — Milgram lemma 20
Legendrc polynomials 237
Legendre differential equation 237
Legendre differential equation, associated 237
Legendre function, associated 238
Linear sampling method 397
Linear sampling method, implementation 402
Linear sampling method, mathematics 422
Linear sampling method, numerical results 405
Lipschitz domain 38
Lois’ variational method 371
LSM see “Linear sampling method”
Matrix problem 334
Maxwell’s equations, time dependent 2
Maxwell’s equations, time harmonic 7
Mei series 256 259
Mesh parameter h 112
Minimum rule 218
Mixed problem 22
Mixed reciprocity 411
Morozov discrepancy principle 402
NEA see “Normalized echo area”
Neumann series 23
Non-conforming elements 200
Normal vector 39
Normalized echo area 392
NtD map see “Calderon operator”
Ohm’s Law 6
Operator, adjoint 18
Operator, bounded 18
Operator, collectively compact 32
Operator, compact 23
Operator, continuous 18
Operator, dual 19
Operator, linear 18
Operator, norm 18
Operator, nullspace 18
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -coercivity
-coercivity 
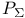



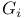
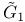
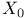 into
into 
 into
into  into
into 
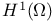 conforming, hexahedra
conforming, hexahedra 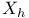 in X
in X 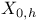
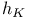 and
and 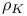
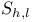
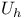




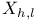
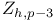
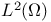 conforming, hexahedra
conforming, hexahedra 
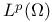
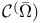

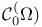
 ,
, 
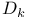
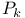 ,
, 
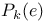 ,
, 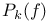

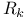
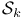


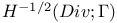
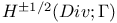
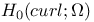
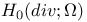

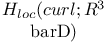


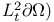
 ,
,  ,
,  ,
, 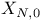 ,
, 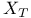 ,
, 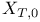


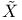
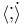



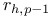





![$[\dot]_N$](/math_tex/1c0a583884211410cb3ba4edd0a80a2682.gif)
![$[\dot]_T$](/math_tex/2ce036c29ce8ca8cdabbc3b00083db8882.gif)