|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ruppert W. — Compact Semitopological Semigroups: An Intrinsic Theory |
|
|
 |
| Предметный указатель |
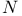 , weak almost periodic compactification of 241 , weak almost periodic compactification of 241
 (=one-point compactification of (=one-point compactification of  ) 1 ) 1
 , Ellis compactification of 190 , Ellis compactification of 190
 , weak almost periodic compactification of 155 , weak almost periodic compactification of 155
Abelian subsemigroup, closure of - 10
Action, affine 99
Action, distal 99
Action, effective 58 81
Action, equicontinuous 70
Action, jointly continuous 11 52—63 95
Action, left [right] 11 124
Action, minimal 57 67 95
Action, minimal, of a cone 94
Action, minimal, of a group 80 81 206
Action, minimal, of a semigroup 52—55 61 62 63 67 90 91 92 93 94 95 96
Action, minimal, of a semilattice 238 239
Action, separately continuous 11
Adjoint functor theorem 102 165
Adjunction of a zero 35 43
Adjunction of an ideal 35 121
Adjunction of an identity 9 56
Ahre 46 244
Alexander — Cech cohomology of ideal 19 20
Alexander — Cech cohomology of M-semigroups 206—211 218 219 220 222 228 229
Alexander — Cech cohomology of semilattices of groups 202 203
Alexander — Cech cohomology, not concentrated on M(S) 2 2
Alexandroff 89 244
Almost periodic compactification 102 103 104 105 115 125
Almost periodic function 113 161
Arens multiplication 165
Asplund 100 244
Automorphism of weak almost periodic compactification 123
Baire 4 47 72 92 94 240 244
Baire space 47 72 89 90 92 96 97 239
Baker 45 59 164 165 244
Banach 97 244
Band 64 65
Berglund 44 45 46 85 100 109 110 165 231 233—235 244
Betti numbers 203 206 207 210 220 229
Bicontinuous 8 57 99 170 178
Bicyclic semigroup 37 38 40 41
Boundary 80 168
Bourbaki 48 56 90 94 97 98 107 126 245
Bredon 206 207 245
Brouwer 197
Brown, G. 154 165 241 245
Brunner, N. 2 40
Burckel 44 110 245
Butcher 45 164 245
C-set 237
Cancellative 50 13 14
Cech, complete 93
Cell,semigroup on a 238
Central 22 15 162
Centric 9 45 81 130—140 162
Centrum 10 153 154 155 156
Chain 13 16 103 239
Chain, 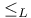 , , 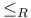 - 16 18 41 70 - 16 18 41 70
Chain, maximal 13 16—18 41 64 70 96
Chernoff 99 245
Chou 164 166 245
Christensen 97 100 246
Circle,semigroup on the 74 176 204 231
Clifford 9 37 45 46 178 246
Compactification, almost periodic 102 103 104 105 115 125
Compactification, dynamical 101 113 125
Compactification, Ellis 202 10 107 113 117 164 190
Compactification, Ellis, map 101
Compactification, Ellis, semigroup 101
Compactification, Ellis, semitopological- 101
Compactification, Stone — Cech- 102 164 165
Compactification, topological- 104 103
Compactification, weak almost periodic see weak almost periodic
Complete group 56 64 95 242
Complete lattice 15
Complete semilattice 15
Completely metrizable space (and joint continuity) 90 96
Condition (o) 200
Cone, action of a convex- 94
Confinement principle 92—94 99
Congruence 33 34
Congruence, induced by normal subsemigroup 34
Congruence, Rees 34
Connected ideals 19 32
Cup product 206
Cutpoint 173 228 236
de Leeuw 43 164 166 246
Decomposition of M-semigroups 208 212—220 229
Decomposition of weakly almost periodic function 113 161 164
Direct product 38 216 217 218 223
Directed 21 14 15
Dissipative 113 161
Distal 99
Dorroh 98 246
Dotted disc topology 87
Dunkl 165 246
Dynamical compactification 44 101 113
Eberhart 43 246
Eberlein 164 246
Eckmann 2 36
Effective action 58 81
Ellis 43 44 46 62 95 97 98 99 164 246
Ellis compactification 102 103 105 107 1 117 164 165
Ellis — Lawson, Theorem of 62 95
Enveloping semigroup 44
Euclidean neighborhood (of 1) 160 170
Euler — Poincare characteristic 206 209 211 228 236
Extension of inversion 104 1
Extension, problem 107 117—123
Extension, Rees- 34
Filtered 23 14 15
Fixed point free approach (to Ryll — Nardzewski's Theorem) 100
Flor 44 46 164 165 247
Fluchtvektor (flight vector) 164
Fort 98 247
Free compact semitopological semigroups 242
Freudental 127 188 247
Frolik 97 247
Function spaces 107—114
Furstenberg 99 247
Gierz 98
Glicksberg 43 164 166 246
Green's relations, R, L, D, I, H 9 12 40 41 54 58 59 66 130 232 234 240
Green's relations, R, L, D, I, H, are not closed 10 12
Grothendieck 110 247
Group of units 9 168 174
Group with zero 150—152 219 242
Group, semitopological, but not topological 86—89
Gysin 236
Hahn 90 247
Halmos 28 247
Hansel 98 239
Helgason 138 247
Helmer 98 248
Hewitt 127
Hilbert space 166
Hille 43 248
Hindman 165
Hochschild 132 151 158 209 210 248
Hoffmann — Jorgensen 100
Hofmann 5 40 41 44 45 46 80 85 98 109 110 171 173 231 242 243 248
Hofmann — Mostert method 171—174
Hopf 236
Hunter 231
Hurewicz 198 248
Husain 44 248
I-semigroup 75 76
Ideal, cohomology of 19
Ideal, left [right] 9 10 19—32
Ideal, maximal proper 235
| Ideal, minimal 21 32 42
Ideal, two-sided 9 10 19—32 200
Idempotents 9 12—18 45 64 65 66 70 103 130 137 193 199 220 243
Idempotents, central 199 228 243
Idempotents, existence of 12 45
Idempotents, form closed set 64 200 243
Idempotents, infimum [supremum] of 15
Idempotents, maximal 13 14 18 64 95 193 201 204
Idempotents, minimal 21—26 28 29
Idempotents, number of- 155 159 163 165 210 211 229
Imbedding problems 115—123 161 242
Inside point (=intrinsic point) 171
Interchanging left and right 33
Interval semigroup 56 65 74—80 176 177 231
Inversion, continuity of, in a group 64 90 95 9
Inversion, continuity of, in a semilattice of groups 64 95
Inversion, extension of- 104 161
Irreducible action 149
Irreducible semigroup 233 234
Isbell 115 248
Isotropy group 81 124 128 129 132—140 146 193—199 209 210 212—219 228 229 243
Iwasawa decomposition 138 203 209
Jacobs 164 248
Joint continuity 8 47—100 238—240
Joint continuity and equicontinuity 47 53
Joint continuity of actions 62 66 67 95 96
Joint continuity of group multiplication 43 73 74 89 95
Joint continuity of multiplication in semigroups on subsets of IR 72—74
Joint Continuity Theorem 63 95 99
Joint Continuity Theorem, metrizable version 55 56 89 95
Joint continuity, (points of)form residual subset 48 49
Joint discontinuity.measure of 240
Junghenn 44 45 165 248
k-space 9 8
Katetov 117 248
Keimel 9 8
Kelley 17 248
Knapp 44 164 249
Koshiba 97 249
L-semigroup 186 18 194 222 228 243
Lattice 15 162 217 220 229 243
Lawson 45 62 95 97 98 99 100 230 231 238 239 249
Left continuous 8
Left group 22
Left identity 77 78 79 80
Left zero semigroup 22 28 78
Lerner 165 248
Lie groups 128 129 133—140 141—149 195
Local cross-section 193—199
Local weak cutpoint 173 228 236
Locally compact semigroup with H(1) not a topological group 98
Locally compact semigroup, one-point compactification of 35
Locally surjective 54
Lower bound of a set of idem-potents 13—18
M-semigroup 186 186—182
Madison 230 249
Magnifying elements 232
Manifolds with boundary, semigroups on- 40 80—85 96 203
Manifolds, semigroups on 126 127 168—231 237
Massey 171 249
Mautner phenomenon 166
Maximal, -subgroups 21 24—29 64 95 160 198 200 205 229 243
Maximal, almost periodic 125
Maximal, ideals 235
Maximal, idempotents 13 14 18 64 95 193 201 204
Measure algebra 43
Meet-continuous 15
Milnes 44 45 59 164 165 249
Minimal ideal 21—32 46 58 59 64 95 96 105 242
Minimal ideal, general structure theorem 24 25
Minimal ideal, joint continuity in- 24—32 50
Minimal idempotent 13 14 21 46
Minimally weakly almost periodic 166
Mislove 9 8
Mitchell 102 164 249
Monoid(=semigroup with identity) on locally connected space 174 see
Monoid(=semigroup with identity) on manifold with boundary 80—85 95 96 168—232
Monoid(=semigroup with identity), spaces forbidden for semitopological 236 237
Monothetic 241
Montgomery 43 90 96 99 126 128 189
Moore 166 250
Moran 154 165 241 245
Moriya 97 250
Mostert 5 41 45 80 85 98 168 171 173 230 248 250
Mostert — Shields method 168
Multiplicative 14
Namioka 44 45 94 98 100 244 250
Namioka's Theorem 9 8
Niemitzky plane 87
Normal quotient 34
Normal subset of a semigroup 9 10 45
One-parameter semigroup 233
One-point compactification 1 31 35 43 176 205
Opposite semigroup 33
Order relations on idempotents 12 13—18 45 58
Ordered semigroup 72 74 75
Orientable 203
P(g) 178 183 184 185 213 221 222 231
P-point 164
Paragroup 22 29 42 50
Peripheral 171 168—175 198 234 237
Peripherality concepts 230 234 235
Pinched disc topology 88
Poincare duality space 206
Pre-orders on E(S) 12 13—18 45 58
Precompact 114
Preston 37 45 46 178 244
Productibility 165
Projective space,monoid on a 219 236
Pym 164 250
Quasi-equicontinuous 70
Quotient action 61
Quotient group, weak almost periodic, compactification of 83 106 131
Quotient semigroup 34
R(G) 183 184 185 231
Ramirez 165 246
Real interval semigroup 74
Reductive semigroup 50
Rees extension 34 35>37
Rees quotient 34
Regular semigroup 153 154—160 163
Retract, ideals behaving like- 19
Right continuous 8
Right group 22 29 54
Right identity 77 78 79 80
Right topological, but not semitopological group 39 40
Right topological, but not semitopological semigroup 8 8—10 12—24 26—28 33—40 42 43 44 51 59
Right zero semigroup 22 24 78
Rim 230
Ross 127 248
Ruppert 44 45 46 99 100 125 166 231 199 250 251
Ryll — Nardzewski 6 99 100 251
Ryll — Nardzewski 's Theorem 6 64 96 99 100
Samelson 2 36
Sandwich product 22
Scott 98
Selden 43 246
Semidirect product 38 156 160 223 224 229 243
Semigroup on interval 29 56 72—80
Semigroup on manifold 126 127 168—231 237
Semigroup, bicyclic 37 38 40 41
Semigroup, bisimple 41
Semigroup, compactification 44 101
Semigroup, left[right]zero 22
Semigroup, on manifold with boundary 40 80—85 96 203
Semigroup, regular 153 154—160 163
Semigroup, right topological 8 8—10 12—24 26—28 33—40 42 43 51 59
Semigroup, semitopological 1 8 43 44
Semigroup, semitopological,with no points of joint continuity 50 51
Semigroup, topological- 1 8
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



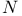 , weak almost periodic compactification of
, weak almost periodic compactification of  (=one-point compactification of
(=one-point compactification of  , Ellis compactification of
, Ellis compactification of 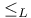 ,
, 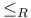 -
-